Условие перпендикулярности.

Две плоскости перпендикулярны друг другу тогда и только тогда, когда их нормальные векторы взаимно перпендикулярны. Поэтому, воспользовавшись условием перпендикулярности двух векторов (см. гл. III, формула (69)), получим

Равенство (9) дает условие перпендикулярности двух плоскостей. Итак, две плоскости перпендикулярны друг другу тогда и только тогда, когда сумма парных произведений одноименных коэффициентов при текущих координатах равна нулю.

Пример 2. Составить уравнение плоскости, проходящей через точку параллельно плоскости

Решение. Напишем уравнение связки плоскостей, проходящих через точку (см. формулу ):

Из плоскостей связки нам нужно выделить ту, которая параллельна на плоскости Для этого воспользуемся условием (8) параллельности плоскостей: Итак, искомые коэффициенты А, В и С должны быть пропорциональны числам Поэтому можно положить . Подставляя найденные значения коэффициентов А, В и С в уравнение

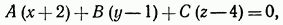
получим

или, после упрощений,

Это и есть уравнение искомой плоскости.

Не нашли, что искали? Воспользуйтесь поиском: