
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Теорема Абеля. Теорема об интервале сходимости степенного ряда. Вычисление радиуса сходимости степенного ряда по коэффициентам ряда
ЛЕКЦИЯ 12
СТЕПЕННЫЕ РЯДЫ
Ранее рассматривались ряды, элементами которых были числа. Рассмотрим теперь ряды, элементами которых являются функции, т.е. ряды вида  где
где 
 − функции, имеющие общую область определения
− функции, имеющие общую область определения  Такие ряды называют функциональными, функции
Такие ряды называют функциональными, функции  называют элементами ряда, а
называют элементами ряда, а 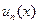 − общим элементом ряда. Например,
− общим элементом ряда. Например,  где
где 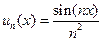 .
.
Ясно, что при подстановке в функциональный ряд конкретного значения  получается числовой ряд
получается числовой ряд 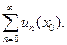 Если этот ряд сходится, то точку
Если этот ряд сходится, то точку 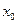 называют точкой сходимости для ряда
называют точкой сходимости для ряда 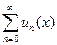 . Все точки сходимости образуют область сходимости функционального ряда. Говорят, что ряд
. Все точки сходимости образуют область сходимости функционального ряда. Говорят, что ряд 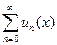 абсолютно сходится на
абсолютно сходится на 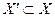 , если сходится ряд
, если сходится ряд  ,
,  . Для функциональных рядов важную роль играет понятие равномерной сходимости на
. Для функциональных рядов важную роль играет понятие равномерной сходимости на 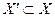 . Говорят, что ряд
. Говорят, что ряд 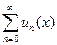 равномерно сходится на
равномерно сходится на 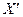 , если для любого
, если для любого 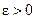 и любого натурального
и любого натурального  существует номер
существует номер 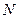 такой, что при всех
такой, что при всех  неравенство
неравенство 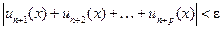 выполнено при всех
выполнено при всех  .
.
Пусть ряд 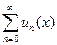 , где
, где 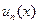 непрерывные функции на
непрерывные функции на  , равномерно сходится на
, равномерно сходится на  и имеет место равенство
и имеет место равенство 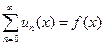 ,
, 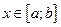 . Тогда
. Тогда 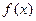 − непрерывная функция и этот ряд можно поэлементно интегрировать на
− непрерывная функция и этот ряд можно поэлементно интегрировать на  , т.е. справедливо равенство:
, т.е. справедливо равенство: 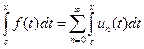 , и в частности
, и в частности 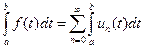 где
где  .
.
Важным частным случаем функциональных рядов являются степенные ряды, т.е. ряды вида 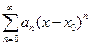 , где
, где 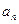 − числовые коэффициенты,
− числовые коэффициенты, 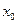 − фиксированное значение переменной
− фиксированное значение переменной 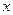 . Например,
. Например, 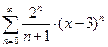 . Здесь
. Здесь 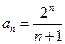 ,
,  . Если
. Если 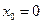 , то получаем ряд вида
, то получаем ряд вида  . С другой стороны ряд
. С другой стороны ряд 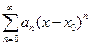 заменой
заменой 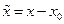 можно свести к ряду
можно свести к ряду 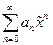 . Поэтому результаты, полученные для ряда
. Поэтому результаты, полученные для ряда  справедливы для ряда
справедливы для ряда 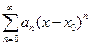 и наоборот.
и наоборот.
Теорема Абеля. Теорема об интервале сходимости степенного ряда. Вычисление радиуса сходимости степенного ряда по коэффициентам ряда
Структура области сходимости степенного ряда устанавливается с помощью теоремы Абеля.
Теорема 1. (теорема Абеля). Если степенной ряд  сходится при значении
сходится при значении 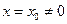 , то он абсолютно сходится при всех значениях
, то он абсолютно сходится при всех значениях 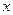 таких, что
таких, что  . Если степенной ряд
. Если степенной ряд  расходится при
расходится при  , то он расходится при всех значениях
, то он расходится при всех значениях 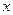 таких, что
таких, что  .
.
Из теоремы Абеля вытекает следующая теорема об интервале сходимости степенного ряда.
Теорема 2. Для ряда  существует такое число
существует такое число  , что при
, что при  ряд абсолютно сходится, а при
ряд абсолютно сходится, а при 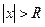 – расходится.
– расходится.
Число 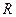 получило название радиуса сходимости, а интервал
получило название радиуса сходимости, а интервал  – интервала сходимости степенного ряда. На концах интервала, т.е. при
– интервала сходимости степенного ряда. На концах интервала, т.е. при 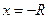 и
и 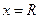 ряд может как сходиться, так и расходиться. Если
ряд может как сходиться, так и расходиться. Если 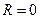 , то ряд сходится в одной точке:
, то ряд сходится в одной точке: 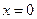 . Если
. Если  , то ряд сходится для
, то ряд сходится для 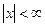 , т.е. на всей числовой прямой.
, т.е. на всей числовой прямой.
Для ряда 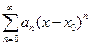 аналогичные результаты имеют вид: существует такое число
аналогичные результаты имеют вид: существует такое число  , что при
, что при 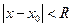 ряд абсолютно сходится, а при
ряд абсолютно сходится, а при 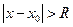 − расходится. В точках
− расходится. В точках 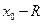 и
и  ряд может как сходиться, так и расходиться. Если
ряд может как сходиться, так и расходиться. Если 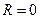 , то ряд сходится в одной точке:
, то ряд сходится в одной точке: 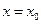 . Если
. Если  , то ряд сходится на всей числовой прямой.
, то ряд сходится на всей числовой прямой.
Из сказанного ясно, что важно научиться находить радиус сходимости 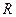 . Если ряд имеет вид
. Если ряд имеет вид  или
или 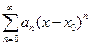 (т.е. содержит все степени переменной), то можно воспользоваться формулой
(т.е. содержит все степени переменной), то можно воспользоваться формулой
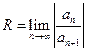
или формулой
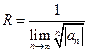
В противном случае для отыскания 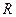 применяют признак Даламбера или Коши непосредственно к рядам
применяют признак Даламбера или Коши непосредственно к рядам 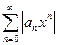 или
или  .
.
Не нашли, что искали? Воспользуйтесь поиском: