Арифметические операции над степенными рядами

Следует отметить, что на любом отрезке внутри интервала сходимости ряды 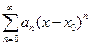и сходятся равномерно. Поскольку функции и непрерывны при любом 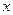, то и суммы указанных рядов непрерывны, а также возможно поэлементное интегрирование рядов в области равномерной сходимости. При этом вновь полученные степенные ряды также равномерно сходятся, а радиус сходимости 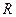не изменяется. Не изменяется радиус сходимости и при поэлементном дифференцировании степенных рядов, т.е. если , то для .

Рассмотрим теперь ряды 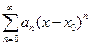и , имеющие радиусы сходимости и .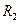

При умножении ряда на число вновь полученный ряд имеет тот же радиус сходимости, т.е. ряд сходится на , а ряд − на .

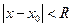Сложение двух степенных рядов выполняют так же, как сложение двух многочленов, т.е. сложением коэффициентов при одинаковых степенях переменной: . Суммарный ряд сходится для , где .

Не нашли, что искали? Воспользуйтесь поиском: