Сходящиеся, абсолютно сходящиеся и условно сходящиеся комплексные ряды

ЛЕКЦИЯ 14

КОМПЛЕКСНЫЕ РЯДЫ

Сходящиеся, абсолютно сходящиеся и условно сходящиеся комплексные ряды

Выражение вида , где , , , называется комплексным числовым рядом.

Величина называется частичной суммой ряда , а числа – его элементами.

Если существует конечный предел , то говорят, что этот ряд сходится и число называют его суммой. В противном случае ряд расходится.

Сходимость комплексного ряда к сумме равносильна сходимости двух вещественных рядов и к суммам А и В соответственно.

Если сходится ряд , составленный из модулей элементов ряда , то и этот ряд также сходится. В этом случае ряд называют абсолютно сходящимся.

Ряд называют условно сходящимся, если этот ряд сходится, но ряд расходится.

Абсолютная сходимость ряда влечет за собой сходимость обоих рядов и .

Благодаря этому, для комплексных рядов сохраняет свою силу, например, признак Даламбера.

При исследовании на сходимость числовых рядов с комплексными элементами предлагается следующая методика решения:

1) для ряда , где , составить ряд и изучить его на сходимость;

2) в случае отсутствия абсолютной сходимости изучить ряды и .

Пример 1. Исследовать сходимость ряда с комплексными элементами: .

□ 1) Для исследования на абсолютную сходимость применим признак Даламбера:

составим ;

составим ;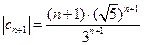

вычислим ;

полученный результат 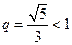, поэтому, по признаку Даламбера, ряд сходится, а исходный ряд абсолютно сходится.

2) Дальнейшее исследование не требуется. ■

Пусть комплексная переменная принимает всевозможные значения из некоторого множества комплексно плоскости. Если с каждым значением z из множества Z сопоставляется одно или несколько значений другой комплексной переменной , то последнюю называют (соответственно, однозначной или многозначной) функцией от z на множестве Z и обозначают: .

Примерами однозначных функций могут служить , 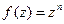. В качестве примеров многозначных функций можно назвать , .

Ряды вида , элементами которых являются функции от комплексной переменной , определенные в области , называют функциональными.

Значение из множества Z, для которого сходится числовой ряд , называют точкой сходимости функционального ряда. Все точки сходимости образуют область сходимости.

Не нашли, что искали? Воспользуйтесь поиском: