Функции комплексной переменной как суммы абсолютно сходящихся степенных рядов. Формула Эйлера

Ряд вида , где 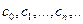– комплексные числовые коэффициенты, а z – переменная, изменяющаяся во всей комплексной плоскости, называют степенным. По аналогии со степенными рядами для действительной переменной, установлено существование такого числа , что для (если ) ряд абсолютно сходится, а для (если ) ряд расходится. Таким образом, если и конечно, то степенной ряд абсолютно сходится внутри круга радиуса R с центром в начале координат и расходится вне этого круга. Например, с помощью признака Даламбера, изучим на абсолютную сходимость ряд .

□ Здесь , , 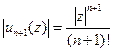тогда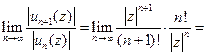 при любом z. Значит, изучаемый ряд сходится абсолютно для .

Ранее было установлено, что при любом вещественном x имеет место разложение .

Если в этом ряде заменить вещественную переменную x комплексной переменной , то получится ряд , про который мы установили, что он сходится, т.е. имеет определенную конечную сумму, во всей плоскости комплексной переменной. Его сумму и принимают, по определению, за значение показательной функции при любом комплексном z, т.е. полагают , . ■

Используя это определение, можно показать, что для любых и справедливо равенство: .

Пусть , где . Тогда .

Если в ряд для подставить вместо z, то получим , или, отделяя вещественную часть от мнимой, .

В полученных рядах легко узнать разложения для 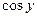и и, таким образом, получить замечательную формулу: , которую называют формулой Эйлера. Итак, если , то .

Пример 2. Вычислить .

□ . ■

Пример 3. Изучить на сходимость ряд .

□ 1) Здесь , тогда

;

Это знакоположительный ряд, который изучим на сходимость с помощью признака сравнения, взяв для сравнения ряд с общим элементом , про который известно, что он сходится. Вычислим .

Следовательно, ряд сходится, а исходный ряд сходится абсолютно.

2) Дальнейшее исследование не требуется. ■

Пример 4. Изучить на сходимость ряд .

□ 1) Здесь , тогда 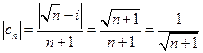; это знакоположительный ряд, который изучим на сходимость с помощью признака сравнения, взяв для сравнения ряд с общим элементом . Известно, что последний ряд расходится. Вычислим .

Следовательно, расходится, а исходный ряд не имеет абсолютной сходимости.

2) Представим 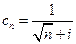в виде , тогда . Для изучения ряда используем признак сравнения, взяв для сравнения ряд , который расходится.

Вычислим , следовательно, ряд расходится.

Ряд 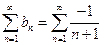ведет себя в смысле сходимости так же, как ряд 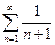. Для изучения этого ряда сравним его с рядом , который расходится.

Вычислим . Следовательно, ряд расходится.

Итак, исходный ряд расходится. ■

Пример 5. Вычислить .

□ По формулам Эйлера, . ■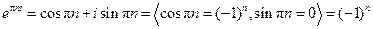

Не нашли, что искали? Воспользуйтесь поиском: