Задание. Найти координаты вектора 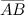 , если , если  Решение.
Решение.  Длина (модуль) вектора
Теоретический материал по теме - длина вектора.
Пример
Задание. Найти длину вектора
Длина (модуль) вектора
Теоретический материал по теме - длина вектора.
Пример
Задание. Найти длину вектора 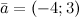 Решение. Используя формулу, получаем:
Решение. Используя формулу, получаем:
 Пример
Задание. Найти длину вектора
Пример
Задание. Найти длину вектора 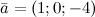 Решение. Используя формулу, получаем:
Решение. Используя формулу, получаем:
 Угол между векторами
Теоретический материал по теме - угол между векторами.
Пример
Задание. Известно, что скалярное произведение двух векторов
Угол между векторами
Теоретический материал по теме - угол между векторами.
Пример
Задание. Известно, что скалярное произведение двух векторов 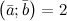 , а их длины , а их длины 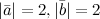 . Найти угол между векторами . Найти угол между векторами  и и  .
Решение. Косинус искомого угла: .
Решение. Косинус искомого угла:
 Пример
Задание. Найти угол между векторами
Пример
Задание. Найти угол между векторами 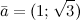 и и  Решение. Косинус искомого угла
Решение. Косинус искомого угла

 Пример
Задание. Найти угол между векторами
Пример
Задание. Найти угол между векторами 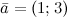 и и  Решение. Косинус искомого угла:
Решение. Косинус искомого угла:
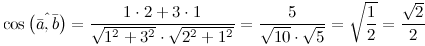
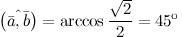 Разложение вектора по ортам координатных осей
Теоретический материал по теме - разложение вектора по ортам.
Пример
Задание. Зная разложения вектора
Разложение вектора по ортам координатных осей
Теоретический материал по теме - разложение вектора по ортам.
Пример
Задание. Зная разложения вектора  по базисной системе векторов: по базисной системе векторов: 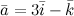 , записать координаты этого вектора в пространстве.
Решение. Коэффициенты при ортах и есть координатами вектора, поэтому из того, что , записать координаты этого вектора в пространстве.
Решение. Коэффициенты при ортах и есть координатами вектора, поэтому из того, что 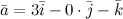 , получаем, что , получаем, что  Пример
Задание. Вектор
Пример
Задание. Вектор  задан своими координатами: задан своими координатами:  . Записать разложение данного вектора по ортам осей координат.
Решение. Координаты вектора - это коэффициенты при ортах координатных осей в разложении вектора по базисной системе векторов, поэтому искомое разложение: . Записать разложение данного вектора по ортам осей координат.
Решение. Координаты вектора - это коэффициенты при ортах координатных осей в разложении вектора по базисной системе векторов, поэтому искомое разложение:
 Скалярное произведение векторов
Теоретический материал по теме - скалярное произведение векторов.
Пример
Задание. Вычислить скалярное произведение векторов
Скалярное произведение векторов
Теоретический материал по теме - скалярное произведение векторов.
Пример
Задание. Вычислить скалярное произведение векторов  и и  , если их длины соответственно равны 2 и 3, а угол между ними 60°.
Решение. Так как из условия , если их длины соответственно равны 2 и 3, а угол между ними 60°.
Решение. Так как из условия  , ,  , а , а 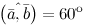 , то , то
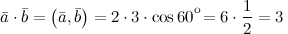 Пример
Задание. Найти скалярное произведение векторов
Пример
Задание. Найти скалярное произведение векторов  и и 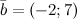 Решение. Скалярное произведение
Решение. Скалярное произведение
 Векторное произведение векторов
Теоретический материал по теме - векторное произведение векторов.
Пример
Задание. Найти векторное произведение векторов
Векторное произведение векторов
Теоретический материал по теме - векторное произведение векторов.
Пример
Задание. Найти векторное произведение векторов  и и  Решение. Составляем определитель и вычисляем его:
Решение. Составляем определитель и вычисляем его:
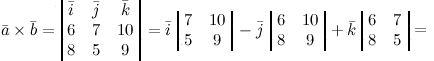

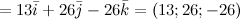 14)Чтобы разложить, вектор b по базисным векторам a1,..., an, необходимо найти коэффициенты x1,..., xn, при которых линейная комбинация векторов a1,..., an равна вектору b:
x1a1 +... + xnan = b,
при этом коэффициенты x1,..., xn, называются координатами вектора b в базисе a1,..., an.
Док-во-любой вектор в пространстве может быть единственным образом разложен по базису е1, е2, е3, т. е. вектор а=х1е1+х2е2+х3е3. вектор а представляет собой линейную комбинацию векторов е1, е2, е3
14)Чтобы разложить, вектор b по базисным векторам a1,..., an, необходимо найти коэффициенты x1,..., xn, при которых линейная комбинация векторов a1,..., an равна вектору b:
x1a1 +... + xnan = b,
при этом коэффициенты x1,..., xn, называются координатами вектора b в базисе a1,..., an.
Док-во-любой вектор в пространстве может быть единственным образом разложен по базису е1, е2, е3, т. е. вектор а=х1е1+х2е2+х3е3. вектор а представляет собой линейную комбинацию векторов е1, е2, е3
|
отрезок- это часть прямой линии, ограниченная двумя точками - началом и концом.Длина отрезка это расстояние от одной точки до другой.
разделить отрезок в заданном отношении, необходимо в этом отношении разделить его проекции. На рисунке отрезок MN поделен точкой К в отношении MK:KN=1:4  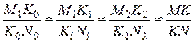 16)Любую плоскость можно задать уравнением плоскости первой степени вида Ax+By+Cz+D=0
где A, B и C не могут быть одновременно равны нулю.
Способы задания плоскости:
Через точку и вектор нормали - Если в пространстве задана точка М0(х0, у0, Z0), то уравнение плоскости, проходящей через точку М0 перпендикулярно вектору нормали (A, B, C) имеет вид:
A(X – X0) + B(Y – Y0) + C(Z – Z0) = 0.
Через 3 точки- Если в пространстве задана точка М0(х0, у0, Z0), то уравнение плоскости, проходящей через точку М0 перпендикулярно вектору нормали (A, B, C) имеет вид:
A(X – X0) + B(Y – Y0) + C(Z – Z0) = 0.
Нормальное уравнение плоскости-
16)Любую плоскость можно задать уравнением плоскости первой степени вида Ax+By+Cz+D=0
где A, B и C не могут быть одновременно равны нулю.
Способы задания плоскости:
Через точку и вектор нормали - Если в пространстве задана точка М0(х0, у0, Z0), то уравнение плоскости, проходящей через точку М0 перпендикулярно вектору нормали (A, B, C) имеет вид:
A(X – X0) + B(Y – Y0) + C(Z – Z0) = 0.
Через 3 точки- Если в пространстве задана точка М0(х0, у0, Z0), то уравнение плоскости, проходящей через точку М0 перпендикулярно вектору нормали (A, B, C) имеет вид:
A(X – X0) + B(Y – Y0) + C(Z – Z0) = 0.
Нормальное уравнение плоскости-  Двугранный угол между плоскостями равен углу образованному нормальными векторами этих плоскостей.
Двугранный угол между плоскостями равен углу образованному прямыми l1 и l2, лежащими в соответствующих плоскостях и перпендикулярными линии пересечения плоскостей.
Формула для вычисления угла между плоскостями
Если заданы уравнения плоскостей A1x + B1y + C1z + D1 = 0 и A2x + B2y + C2z + D2 = 0, то угол между плоскостями можно найти, используя следующую формулу
Двугранный угол между плоскостями равен углу образованному нормальными векторами этих плоскостей.
Двугранный угол между плоскостями равен углу образованному прямыми l1 и l2, лежащими в соответствующих плоскостях и перпендикулярными линии пересечения плоскостей.
Формула для вычисления угла между плоскостями
Если заданы уравнения плоскостей A1x + B1y + C1z + D1 = 0 и A2x + B2y + C2z + D2 = 0, то угол между плоскостями можно найти, используя следующую формулу
| cos α =
| |A1·A2 + B1·B2 + C1·C2|
| | √A12 + B12 + C12√A22 + B22 + C22
| | | | Расстояние от точки до плоскости — равно длине перпендикуляра, опущенного из точки на плоскость.
Формула для вычисления расстояния от точки до плоскости
Если задано уравнение плоскости Ax + By + Cz + D = 0, то расстояние от точки M(Mx, My, Mz) до плоскости можно найти, используя следующую формулу:
| d =
| |A·Mx + B·My + C·Mz + D|
| | √A2 + B2 + C2
|
17) Всякое уравнение первой степени относительно координат x, y, z
Ax + By + Cz +D = 0 (3.1)
задает плоскость, и наоборот: всякая плоскость может быть представлена уравнением (3.1), которое называется уравнением плоскости.
Вектор n (A, B, C), ортогональный плоскости, называется нормальным вектором плоскости. В уравнении (3.1) коэффициенты A, B, C одновременно не равны 0.
Особые случаи уравнения (3.1):
1. D = 0, Ax+By+Cz = 0 - плоскость проходит через начало координат.
2. C = 0, Ax+By+D = 0 - плоскость параллельна оси Oz.
3. C = D = 0, Ax +By = 0 - плоскость проходит через ось Oz.
4. B = C = 0, Ax + D = 0 - плоскость параллельна плоскости Oyz.
Уравнения координатных плоскостей: x = 0, y = 0, z = 0.
Прямая в пространстве может быть задана:
1) как линия пересечения двух плоскостей,т.е. системой уравнений:
A1 x + B1 y + C1 z + D1 = 0, A2 x + B2 y + C2 z + D2 = 0
точкой M1(x1, y1, z1), ей принадлежащей, и вектором a (m, n, р), ей коллинеарным. Тогда прямая определяется уравнениями:
 . .
Уравнения (3.4) называются каноническими уравнениями прямой.
Вектор a называется направляющим вектором прямой.
Параметрические уравнения прямой получим, приравняв каждое из отношений (3.4) параметру t:
x = x1 +mt, y = y1 + nt, z = z1 + рt.
Составьте канонические уравнения прямой:
5x + y + z = 0, 2x + 3y - 2z + 5 = 0.
Решение. Канонические уравнения прямой имеют вид:

где m, n, р - координаты направляющего вектора прямой, x1, y1, z1 - координаты какой-либо точки, принадлежащей прямой. Прямая задана как линия пересечения двух плоскостей. Чтобы найти точку, принадлежащую прямой, фиксируют одну из координат (проще всего положить, например, x=0) и полученную систему решают как систему линейных уравнений с двумя неизвестными. Итак, пусть x=0, тогда y + z = 0, 3y - 2z+ 5 = 0, откуда y=-1, z=1. Координаты точки М(x1, y1, z1), принадлежащей данной прямой, мы нашли: M (0,-1,1). Направляющий вектор прямой легко найти, зная нормальные векторы исходных плоскостей n 1(5,1,1) и n 2(2,3,-2). Тогда

Канонические уравнения прямой имеют вид: x/(-5) = (y + 1)/12 =
= (z - 1)/13.
2. 18. В пучке, определяемом плоскостями 2х-у+5z-3=0 и х+у+2z+1=0, найти две перпендикулярные плоскости, одна из которых проходит через точку М(1,0,1).
Решение. Уравнение пучка, определяемого данными плоскостями, имеет вид u(2х-у+5z-3) + v(х+у+2z+1)=0, где u и v не обращаются в нуль одновременно. Перепишем уравнение пучка следующим образом:
(2u +v)x + (- u + v)y + (5u +2v)z - 3u + v = 0.
Для того, чтобы из пучка выделить плоскость, проходящую через точку М, подставим координаты точки М в уравнение пучка. Получим:
(2u+v)1 + (-u + v)0 + (5u + 2v)1 -3u + v =0, или v = - u.
Тогда уравнение плоскости, содержащей M, найдем, подставив v = - u в уравнение пучка:
u(2x-y +5z - 3) - u (x + y +2z +1) = 0.
Т.к. u0 (иначе v=0, а это противоречит определению пучка), то имеем уравнение плоскости x-2y+3z-4=0. Вторая плоскость, принадлежащая пучку, должна быть ей перпендикулярна. Запишем условие ортогональности плоскостей:
(2u+ v)1 + (v - u)(-2) + (5u +2v)3 = 0, или v = - 19/5u.
Значит, уравнение второй плоскости имеет вид:
u(2x -y+5z - 3) - 19/5 u(x + y +2z +1) = 0 или 9x +24y + 13z + 34 = 0.
* Угол между прямой и плоскостью, пересекающей эту прямую и не перпендикулярной к ней, - это угол между прямой и ее проекцией на эту плоскость.
Не нашли, что искали? Воспользуйтесь поиском:
|

 правая, то их смешанное произведение равно объему параллелепипеда построенного на этих векторах:
правая, то их смешанное произведение равно объему параллелепипеда построенного на этих векторах: 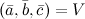 . В случае левой тройки
. В случае левой тройки  смешанное произведение указанных векторов равно объему параллелепипеда со знаком минус:
смешанное произведение указанных векторов равно объему параллелепипеда со знаком минус:  . Если
. Если  ,
,  и
и  компланарны, то их смешанное произведение равно нулю.
компланарны, то их смешанное произведение равно нулю. ,
,  и
и  равен модулю смешанного произведения этих векторов:
равен модулю смешанного произведения этих векторов:
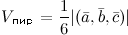


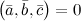
 . Если же
. Если же  , то векторы
, то векторы  ,
,  и
и  образуют левую тройку векторов.
образуют левую тройку векторов.



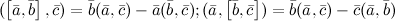
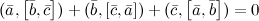
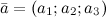 ,
,  и
и 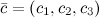 заданы своими координатами, то их смешанное произведение вычисляется по формуле
заданы своими координатами, то их смешанное произведение вычисляется по формуле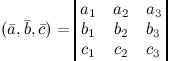
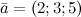 ,
,  ,
, 
 ,
,  и
и  :
:
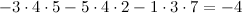

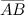 , если
, если  Решение.
Решение.  Длина (модуль) вектора
Теоретический материал по теме - длина вектора.
Пример
Задание. Найти длину вектора
Длина (модуль) вектора
Теоретический материал по теме - длина вектора.
Пример
Задание. Найти длину вектора 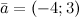 Решение. Используя формулу, получаем:
Решение. Используя формулу, получаем:
 Пример
Задание. Найти длину вектора
Пример
Задание. Найти длину вектора 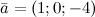 Решение. Используя формулу, получаем:
Решение. Используя формулу, получаем:
 Угол между векторами
Теоретический материал по теме - угол между векторами.
Пример
Задание. Известно, что скалярное произведение двух векторов
Угол между векторами
Теоретический материал по теме - угол между векторами.
Пример
Задание. Известно, что скалярное произведение двух векторов 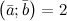 , а их длины
, а их длины 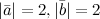 . Найти угол между векторами
. Найти угол между векторами  Пример
Задание. Найти угол между векторами
Пример
Задание. Найти угол между векторами 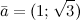 и
и  Решение. Косинус искомого угла
Решение. Косинус искомого угла

 Пример
Задание. Найти угол между векторами
Пример
Задание. Найти угол между векторами 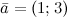 и
и  Решение. Косинус искомого угла:
Решение. Косинус искомого угла:
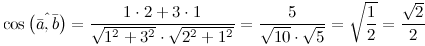
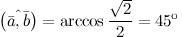 Разложение вектора по ортам координатных осей
Теоретический материал по теме - разложение вектора по ортам.
Пример
Задание. Зная разложения вектора
Разложение вектора по ортам координатных осей
Теоретический материал по теме - разложение вектора по ортам.
Пример
Задание. Зная разложения вектора 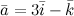 , записать координаты этого вектора в пространстве.
Решение. Коэффициенты при ортах и есть координатами вектора, поэтому из того, что
, записать координаты этого вектора в пространстве.
Решение. Коэффициенты при ортах и есть координатами вектора, поэтому из того, что 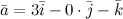 , получаем, что
, получаем, что  Пример
Задание. Вектор
Пример
Задание. Вектор  . Записать разложение данного вектора по ортам осей координат.
Решение. Координаты вектора - это коэффициенты при ортах координатных осей в разложении вектора по базисной системе векторов, поэтому искомое разложение:
. Записать разложение данного вектора по ортам осей координат.
Решение. Координаты вектора - это коэффициенты при ортах координатных осей в разложении вектора по базисной системе векторов, поэтому искомое разложение:
 Скалярное произведение векторов
Теоретический материал по теме - скалярное произведение векторов.
Пример
Задание. Вычислить скалярное произведение векторов
Скалярное произведение векторов
Теоретический материал по теме - скалярное произведение векторов.
Пример
Задание. Вычислить скалярное произведение векторов  ,
,  , а
, а 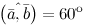 , то
, то
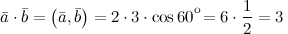 Пример
Задание. Найти скалярное произведение векторов
Пример
Задание. Найти скалярное произведение векторов  и
и 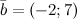 Решение. Скалярное произведение
Решение. Скалярное произведение
 Векторное произведение векторов
Теоретический материал по теме - векторное произведение векторов.
Пример
Задание. Найти векторное произведение векторов
Векторное произведение векторов
Теоретический материал по теме - векторное произведение векторов.
Пример
Задание. Найти векторное произведение векторов  и
и  Решение. Составляем определитель и вычисляем его:
Решение. Составляем определитель и вычисляем его:
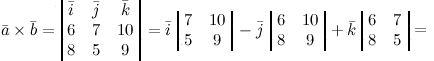

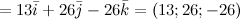 14)Чтобы разложить, вектор b по базисным векторам a1,..., an, необходимо найти коэффициенты x1,..., xn, при которых линейная комбинация векторов a1,..., an равна вектору b:
x1a1 +... + xnan = b,
при этом коэффициенты x1,..., xn, называются координатами вектора b в базисе a1,..., an.
Док-во-любой вектор в пространстве может быть единственным образом разложен по базису е1, е2, е3, т. е. вектор а=х1е1+х2е2+х3е3. вектор а представляет собой линейную комбинацию векторов е1, е2, е3
14)Чтобы разложить, вектор b по базисным векторам a1,..., an, необходимо найти коэффициенты x1,..., xn, при которых линейная комбинация векторов a1,..., an равна вектору b:
x1a1 +... + xnan = b,
при этом коэффициенты x1,..., xn, называются координатами вектора b в базисе a1,..., an.
Док-во-любой вектор в пространстве может быть единственным образом разложен по базису е1, е2, е3, т. е. вектор а=х1е1+х2е2+х3е3. вектор а представляет собой линейную комбинацию векторов е1, е2, е3

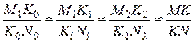 16)Любую плоскость можно задать уравнением плоскости первой степени вида Ax+By+Cz+D=0
где A, B и C не могут быть одновременно равны нулю.
Способы задания плоскости:
Через точку и вектор нормали - Если в пространстве задана точка М0(х0, у0, Z0), то уравнение плоскости, проходящей через точку М0 перпендикулярно вектору нормали (A, B, C) имеет вид:
A(X – X0) + B(Y – Y0) + C(Z – Z0) = 0.
Через 3 точки- Если в пространстве задана точка М0(х0, у0, Z0), то уравнение плоскости, проходящей через точку М0 перпендикулярно вектору нормали (A, B, C) имеет вид:
A(X – X0) + B(Y – Y0) + C(Z – Z0) = 0.
Нормальное уравнение плоскости-
16)Любую плоскость можно задать уравнением плоскости первой степени вида Ax+By+Cz+D=0
где A, B и C не могут быть одновременно равны нулю.
Способы задания плоскости:
Через точку и вектор нормали - Если в пространстве задана точка М0(х0, у0, Z0), то уравнение плоскости, проходящей через точку М0 перпендикулярно вектору нормали (A, B, C) имеет вид:
A(X – X0) + B(Y – Y0) + C(Z – Z0) = 0.
Через 3 точки- Если в пространстве задана точка М0(х0, у0, Z0), то уравнение плоскости, проходящей через точку М0 перпендикулярно вектору нормали (A, B, C) имеет вид:
A(X – X0) + B(Y – Y0) + C(Z – Z0) = 0.
Нормальное уравнение плоскости-  Двугранный угол между плоскостями равен углу образованному нормальными векторами этих плоскостей.
Двугранный угол между плоскостями равен углу образованному прямыми l1 и l2, лежащими в соответствующих плоскостях и перпендикулярными линии пересечения плоскостей.
Формула для вычисления угла между плоскостями
Если заданы уравнения плоскостей A1x + B1y + C1z + D1 = 0 и A2x + B2y + C2z + D2 = 0, то угол между плоскостями можно найти, используя следующую формулу
Двугранный угол между плоскостями равен углу образованному нормальными векторами этих плоскостей.
Двугранный угол между плоскостями равен углу образованному прямыми l1 и l2, лежащими в соответствующих плоскостях и перпендикулярными линии пересечения плоскостей.
Формула для вычисления угла между плоскостями
Если заданы уравнения плоскостей A1x + B1y + C1z + D1 = 0 и A2x + B2y + C2z + D2 = 0, то угол между плоскостями можно найти, используя следующую формулу
 .
.