
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Следствия из второго замечательного предела
1° 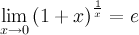
2° 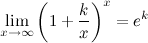
3° 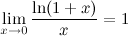
4° 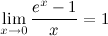
5° 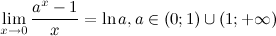
6° 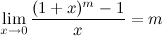
35
 Доказательство
Доказательство

|
36
При переходе к функциям более сложного вида мы обязательно столкнемся с появлением выражений, значение которых не определено. Такие выражения называют неопределенностями.
Основные виды неопределенности:Ноль на ноль  :бесконечность на бесконечность, ноль умножить на бесконечность, бесконечность минус бесконечность, единица в степени бесконечность, ноль в степени ноль, бесконечность в степени ноль. :бесконечность на бесконечность, ноль умножить на бесконечность, бесконечность минус бесконечность, единица в степени бесконечность, ноль в степени ноль, бесконечность в степени ноль.

|
37
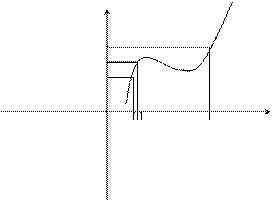
 Функция называется непрерывной на отрезке [ a, b ], если она непрерывна в каждой его точке (в точке а непрерывна справа, в точке b – непрерывна слева).
Основные теоремы о непрерывных функциях
Функция, непрерывная на отрезке [ a, b ], достигает на нём своего наименьшего значения m и наибольшего значения M, то есть существуют такие точки x 1 и x 2этого отрезка, что f (x 1) = m, f (x 2) = M.
Если функция у = f (x) непрерывна на отрезке [ a, b ] и на его концах принимает неравные значения f (а) = А, f (b) = В, А ¹ В, то каково бы ни было число С, заключённое между А и В, найдётся точка с Î [ a, b ] такая, что f (с) = С. Геометрический смысл теоремы иллюстрируется на рис.3. Всякая прямая у = С, где A < C < B (или A > C > B), пересекает график функции у = f (x).
Определение. Если функция f(x) определена в некоторой окрестности точки х0, но не является непрерывной в самой точке х0, то она называется разрывной функцией, а точка х0 – точкой разрыва.
Пример непрерывной функции:
Функция называется непрерывной на отрезке [ a, b ], если она непрерывна в каждой его точке (в точке а непрерывна справа, в точке b – непрерывна слева).
Основные теоремы о непрерывных функциях
Функция, непрерывная на отрезке [ a, b ], достигает на нём своего наименьшего значения m и наибольшего значения M, то есть существуют такие точки x 1 и x 2этого отрезка, что f (x 1) = m, f (x 2) = M.
Если функция у = f (x) непрерывна на отрезке [ a, b ] и на его концах принимает неравные значения f (а) = А, f (b) = В, А ¹ В, то каково бы ни было число С, заключённое между А и В, найдётся точка с Î [ a, b ] такая, что f (с) = С. Геометрический смысл теоремы иллюстрируется на рис.3. Всякая прямая у = С, где A < C < B (или A > C > B), пересекает график функции у = f (x).
Определение. Если функция f(x) определена в некоторой окрестности точки х0, но не является непрерывной в самой точке х0, то она называется разрывной функцией, а точка х0 – точкой разрыва.
Пример непрерывной функции:
 y
f(x0)+e
f(x0)
f(x0)-e
0 x0-D x0 x0+D x y
f(x0)+e
f(x0)
f(x0)-e
0 x0-D x0 x0+D x
 Пример разрывной функции:
y
f(x0)+e
f(x0)
f(x0)-e
x0 x
Определение. Функция f(x) называется непрерывной в точке х0, если для любого положительного числа e>0 существует такое число D>0, что для любых х, удовлетворяющих условию Пример разрывной функции:
y
f(x0)+e
f(x0)
f(x0)-e
x0 x
Определение. Функция f(x) называется непрерывной в точке х0, если для любого положительного числа e>0 существует такое число D>0, что для любых х, удовлетворяющих условию
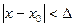 верно неравенство
верно неравенство  .
38
Определение непрерывности функции в билете 37. Теорема Больцмана- Коши- Если функция y=f(x) непрерывна на отрезке [a;b] и принимает на его концах неравные значения f(a)=A и f(b)=В,то на этом отрезке она принимает и все промежуточные значения между А и В.
Следствие из Теоремы Больцана- Коши. Если функция f(x) определена и непрерывна на отрезке [a,b] и на концах этого отрезка принимает разные по знаку значения. Тогда существует такая точка с принадлежащая [а, b] в которой f (c)=0.
Теорема Вейерштрасса - Если функция непрерывна на отрезке, то она достигает на этом отрезке своего наибольшего и наименьшего значений.
Следствие из Теоремы Вейерштрасса. Если функция непрерывна на отрезке, то она ограничена на этом отрезке.
39
Точка .
38
Определение непрерывности функции в билете 37. Теорема Больцмана- Коши- Если функция y=f(x) непрерывна на отрезке [a;b] и принимает на его концах неравные значения f(a)=A и f(b)=В,то на этом отрезке она принимает и все промежуточные значения между А и В.
Следствие из Теоремы Больцана- Коши. Если функция f(x) определена и непрерывна на отрезке [a,b] и на концах этого отрезка принимает разные по знаку значения. Тогда существует такая точка с принадлежащая [а, b] в которой f (c)=0.
Теорема Вейерштрасса - Если функция непрерывна на отрезке, то она достигает на этом отрезке своего наибольшего и наименьшего значений.
Следствие из Теоремы Вейерштрасса. Если функция непрерывна на отрезке, то она ограничена на этом отрезке.
39
Точка  , в которой нарушено хотя бы одно из трех условий непрерывности функции, а именно: Точка , в которой нарушено хотя бы одно из трех условий непрерывности функции, а именно: Точка  , в которой нарушено хотя бы одно из трех условий непрерывности функции, а именно: существует конечный предел функции , в которой нарушено хотя бы одно из трех условий непрерывности функции, а именно: существует конечный предел функции  в точке в точке  ; это предел равен значению функции в точке ; это предел равен значению функции в точке  , т.е. , т.е.  Называется точкой разрыва функции.
Точка разрыва первого рода. Если в точке Называется точкой разрыва функции.
Точка разрыва первого рода. Если в точке  существуют конечные пределы существуют конечные пределы 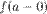 и и  , такие, что , такие, что  , то точка , то точка  называется точкой разрыва первого рода.
Точка разрыва второго рода. Если хотя б один из пределов называется точкой разрыва первого рода.
Точка разрыва второго рода. Если хотя б один из пределов  или или  не существует или равен бесконечности, то точка не существует или равен бесконечности, то точка  называется точкой разрыва второго рода.
40
Производной функции f(x) в точке x0 называется предел отношения приращения функции Δf в этой точке к приращению аргумента Δх, когда последнее стремится к нулю
Физический смысл производной x`(t) от непрерывной функции x(t) в точке t0 – есть мгновенная скорость изменения величины функции, при условии, что изменение аргумента Δt стремится к нулю.нахождение производной называется дифференцированием.
Геометрический смысл производной- производная равна тангенсу угла наклона касательной к графику функции в выбранной точке.
Физический смысл производной- если данную функцию считать зависимостью пути от времени, то её производная в какой-либо точке- это мгновенная скорость в данной точке (т. е. в данный момент времени, поскольку в данном случае точка-это момент времени.
Дифференциалом функции называется линейная относительно называется точкой разрыва второго рода.
40
Производной функции f(x) в точке x0 называется предел отношения приращения функции Δf в этой точке к приращению аргумента Δх, когда последнее стремится к нулю
Физический смысл производной x`(t) от непрерывной функции x(t) в точке t0 – есть мгновенная скорость изменения величины функции, при условии, что изменение аргумента Δt стремится к нулю.нахождение производной называется дифференцированием.
Геометрический смысл производной- производная равна тангенсу угла наклона касательной к графику функции в выбранной точке.
Физический смысл производной- если данную функцию считать зависимостью пути от времени, то её производная в какой-либо точке- это мгновенная скорость в данной точке (т. е. в данный момент времени, поскольку в данном случае точка-это момент времени.
Дифференциалом функции называется линейная относительно  часть приращения функции. Она обозначается как часть приращения функции. Она обозначается как  или или  . Таким образом: . Таким образом:  Геометрический смысл- Дифференциал функции в точке
Геометрический смысл- Дифференциал функции в точке  равен приращению ординаты касательной, проведенной к графику функции в этой точке, соответствующему приращению аргумента равен приращению ординаты касательной, проведенной к графику функции в этой точке, соответствующему приращению аргумента  .
Физический смысл- Дифференциал функции по пути равен расстоянию, которое прошла бы мат. точка за бесконечно малый промежуток времени dx, как если бы она двигалась равномерно со скоростью, равной величине мгновенной скорости в момент времени Х0 .
Физический смысл- Дифференциал функции по пути равен расстоянию, которое прошла бы мат. точка за бесконечно малый промежуток времени dx, как если бы она двигалась равномерно со скоростью, равной величине мгновенной скорости в момент времени Х0
 Функция называется дифференцируемой на интервале- если она дифференцируемая в каждой точке этого интервала.
Если функция
Функция называется дифференцируемой на интервале- если она дифференцируемая в каждой точке этого интервала.
Если функция  дифференцируема в точке X, то она и непрерывна в этой точке. Обратное не гарантировано. дифференцируема в точке X, то она и непрерывна в этой точке. Обратное не гарантировано.
|
41
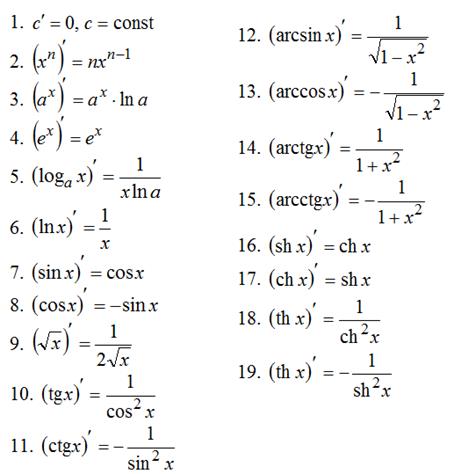
|
42
 Доказательство проведем для производной суммы
Доказательство проведем для производной суммы

|
43
производная сложной функции: f(g(x))' = f'(g(x))·g'(x)
Производная сложной функции



|
44)
Производная функции, заданной параметрически.
Пусть 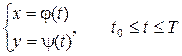
Предположим, что эти функции имеют производные и функция x = j(t) имеет обратную функцию t = Ф(х).
Тогда функция у = y(t) может быть рассмотрена как сложная функция y = y[Ф(х)].
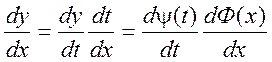
т.к. Ф(х) – обратная функция, то 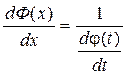
Окончательно получаем: 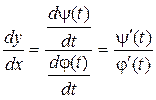
Таким образом, можно находить производную функции, не находя непосредственной зависимости у от х.
Дифференцирование неявных функций
Пусть уравнение  определяет
определяет  как неявную функцию от х.
как неявную функцию от х.
а) продифференцируем по х обе части уравнения  , получим уравнение первой степени относительно
, получим уравнение первой степени относительно  ;
;
б) из полученного уравнения выразим  .
.
 Пример:
Пример:  .
.
45
Теорема Ролля- Если вещественная функция, непрерывная на отрезке [a,b] и дифференцируемая на интервале (a.b), принимает на концах этого интервала одинаковые значения, то на этом интервале найдётся хотя бы одна точка, в которой производная функции равна нулю.
Доказательство - Если функция на отрезке постоянна, то утверждение очевидно, поскольку производная функции равна нулю в любой точке интервала. Если же нет, поскольку значения функции в граничных точках сегмента равны, то согласно теореме Вейерштрасса, она принимает своё наибольшее или наименьшее значение в некоторой точке интервала, то есть имеет в этой точке локальный экстремум, и по лемме Ферма, в этой точке производная равна 0.



|
46
 равило Лопиталя).
Пусть функции
равило Лопиталя).
Пусть функции  и и  удовлетворяют следующим условиям:
1) эти функции дифференцируемы в окрестности точки удовлетворяют следующим условиям:
1) эти функции дифференцируемы в окрестности точки  , кроме, может быть, самой точки , кроме, может быть, самой точки  ;
2) ;
2)  и и  в этой окрестности;
3) в этой окрестности;
3)  ;
4) ;
4)  существует конечный или бесконечный.
Тогда существует и существует конечный или бесконечный.
Тогда существует и  , причем , причем  адание. Найти
адание. Найти  Решение. Получим неопределенность и для решения предела воспользуемся правилом Лопиталя.
Решение. Получим неопределенность и для решения предела воспользуемся правилом Лопиталя.

 Ответ.
Ответ. 
|
47


|
48


|
49



 


|
50

 адание. Найти интервалы выпуклости/вогнутости функции
адание. Найти интервалы выпуклости/вогнутости функции  Решение. Найдем вторую производную заданной функции:
Решение. Найдем вторую производную заданной функции:
 Находим точки, в которых вторая производная равна нулю, для этого решаем уравнение
Находим точки, в которых вторая производная равна нулю, для этого решаем уравнение  : :
 Исследуем знак второй производной слева и справа от полученной точки:
Исследуем знак второй производной слева и справа от полученной точки:
 Так как на промежутке
Так как на промежутке  вторая производная вторая производная  , то на этом промежутке функция , то на этом промежутке функция  выпукла; в силу того, что на промежутке выпукла; в силу того, что на промежутке  вторая производная вторая производная  - функция вогнута. Так как при переходе через точку - функция вогнута. Так как при переходе через точку  вторая производная сменила знак, то эта точка является точкой перегиба графика функции.
Ответ. Точка вторая производная сменила знак, то эта точка является точкой перегиба графика функции.
Ответ. Точка  - точка перегиба графика функции.
На промежутке - точка перегиба графика функции.
На промежутке  функция выпукла, на промежутке функция выпукла, на промежутке  функция вогнута.
51 функция вогнута.
51



|
Не нашли, что искали? Воспользуйтесь поиском: