
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
ГРАФО-АНАЛИТИЧЕСКИЙ МЕТОД
Графоаналитический метод используется в том случае, когда модель линейного программирования можно преобразовать к модели, содержащей две неотрицательные переменные. Тогда графически может быть построена допустимая область  , обычно представляющая собой выпуклый многоугольник в
, обычно представляющая собой выпуклый многоугольник в  .
.
Графоаналитический метод используется в простейшем случае, когда система (объект) определена не более чем двумя переменными или не более чем двумя свободными переменными ( ; где
; где  – ранг матрицы, составленной из коэффициентов в системе ограничений задачи в виде равенств).
– ранг матрицы, составленной из коэффициентов в системе ограничений задачи в виде равенств).
Экстремум целевой функции достигается в одной из вершин этого многоугольника или в каждой точке прямой, соединяющей две соседние вершины (если сторона многоугольника  параллельна линии уровня, задаваемой целевой функцией).
параллельна линии уровня, задаваемой целевой функцией).
Если имеются три переменные, то также можно применить этот метод: прямые заменяются плоскостями, выпуклый многоугольник 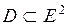 –выпуклым многогранником
–выпуклым многогранником  , линия уровня – поверхностью уровня (плоскостью).
, линия уровня – поверхностью уровня (плоскостью).
Пусть требуется найти неотрицательные значения двух переменных  и
и  , удовлетворяющих
, удовлетворяющих  линейным ограничениям вида
линейным ограничениям вида

и доставляющих минимум (максимум) линейной целевой функции:
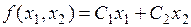 ,
,
что записывается  .
.
Приведем вычислительный алгоритм графоаналитического метода реализации модели линейного программирования.
Алгоритм решения задачи сводится к следующему:
1. На плоскости  построить прямые, уравнения которых получаются в результате замены в ограничениях и знаков неравенств на знак точных равенств.
построить прямые, уравнения которых получаются в результате замены в ограничениях и знаков неравенств на знак точных равенств.
2. Найти полуплоскости, определяемые каждым ограничением задачи.
3. Построить область допустимых решений D, получаемую пересечением полуплоскостей.
4. Построить линию уровня  где
где  , соответствующую целевой функции.
, соответствующую целевой функции.
5. Построить из начала координат вектор  (его смысл – градиент, поэтому это вектор нормали к линии уровня (прямой), соответствующей целевой функции, направленный в сторону наибольшего возрастания функции).
(его смысл – градиент, поэтому это вектор нормали к линии уровня (прямой), соответствующей целевой функции, направленный в сторону наибольшего возрастания функции).
6. Для поиска  передвигать линию уровня в направлении вектора
передвигать линию уровня в направлении вектора  и найти ее последнюю общую точку с областью D. Для поиска
и найти ее последнюю общую точку с областью D. Для поиска 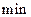 передвигать линию уровня в направлении
передвигать линию уровня в направлении  .
.
7. Определить координаты точки  (
( ) целевой функции – оптимальное решение
) целевой функции – оптимальное решение 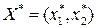 .
.
8. Вычислить значение целевой функции в точке  , то есть
, то есть
 (или
(или  ) в области D.
) в области D.
Замечания
1.Вместо п. 4–6 можно по очереди подставлять в целевую функцию координаты каждой вершины.
2. Если целевая функция имеет вид 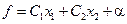 , то п.4 – 7 проводить для функции
, то п.4 – 7 проводить для функции  (постоянная
(постоянная  не влияет на нахождение экстремума, а только сказывается на самой величине
не влияет на нахождение экстремума, а только сказывается на самой величине 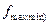 ).
).
3. Если имеются три переменные, то также можно применить этот метод: прямые заменяются плоскостями, выпуклый многоугольник 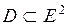 – выпуклым многогранником
– выпуклым многогранником  , линия уровня – поверхностью уровня (плоскостью).
, линия уровня – поверхностью уровня (плоскостью).
Примеры
1. Фирма выпускает два вида тканей. Суточные ресурсы фирмы следующие: 6 единиц производственного оборудования, 8 единиц сырья, 6 единиц энергоресурсов. Расходы каждого типа ресурсов на единицу ткани каждого вида представлены в табл.
Таблица
| Вид ткани | ||
| Ресурсы | ||
| Оборудование | ||
| Сырьё | ||
| Энергоресурсы |
Условная цена единицы ткани первого вида равна 2, а второго вида – 2. Требуется построить математическую модель для нахождения оптимального суточного плана выпуска ткани, обеспечивающего максимальную выручку от реализации готовой продукции. Найти оптимальный план выпуска ткани.
Решение
Введем переменные:
x 1 – объём (количество единиц) производимой ткани первого вида;
x 2 – второго вида;
По смыслу задачи 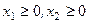 .
.
По условию задачи система ограничений имеет вид

Целевую функцию зададим в виде  .
.
Таким образом, необходимо найти неотрицательные решения системы ограничений, представленные линейными неравенствами, которые обращают в максимум введенную линейную целевую функцию.
Применим для решения задачи алгоритм графоаналитического метода для двух переменных. Для этого на плоскости  в первой четверти построим прямые, уравнения которых получаются в результате замены в системе ограничений знаков неравенств на знак точных равенств
в первой четверти построим прямые, уравнения которых получаются в результате замены в системе ограничений знаков неравенств на знак точных равенств
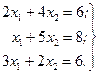
Для построения прямых используем их уравнения в отрезках

Каждая из прямых разобьёт плоскость  на две полуплоскости. Выберем нужные полуплоскости в соответствии с заданной системой ограничений и получим область
на две полуплоскости. Выберем нужные полуплоскости в соответствии с заданной системой ограничений и получим область 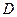 – многоугольник ОАВСЕ.
– многоугольник ОАВСЕ.

|
Построим линию уровня  :
:  , соответствующую целевой функции. Так как ищем максимум целевой функции, то передвигаем линию уровня параллельно вверх и вправо до нахождения ее последней общей точки с областью
, соответствующую целевой функции. Так как ищем максимум целевой функции, то передвигаем линию уровня параллельно вверх и вправо до нахождения ее последней общей точки с областью 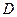 . Такой прямой будет
. Такой прямой будет  , а точкой –
, а точкой –  . Координаты этой точки и дадут оптимальное решение
. Координаты этой точки и дадут оптимальное решение  .
.
Суточная выручка, соответствующая оптимальной организации производства, составляет 4,5 условных единиц.
Отметим, что на производство тканей в указанных количествах:1,5 единиц первого вида и 0,75 – второго, будет задействовано всё производственное оборудование и вся электроэнергия, а сэкономлено 2,75 единиц сырья.
Ответ..
Замечание. Модели, подобные приведённой, относятся к моделям оптимального планирования ЛП.
Не нашли, что искали? Воспользуйтесь поиском: