
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
СИМПЛЕКС–МЕТОД ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Идеей симплекс-метода, основанного на свойствах допустимых и оптимальных решений, является продвижение по выпуклому многограннику ограничений от вершины к вершине, при котором на каждом шаге значение целевой функции улучшается до тех пор, пока не будет достигнут оптимум.
Симплексом тела в к -мерном пространстве в геометрии называется совокупность к +1 его вершин. Так для плоскости к =2 симплексом будут три вершины треугольника. При к =4 – 4 вершины четырехугольника. С учетом данного понятия метод направленного перебора по многограннику ограничений называют симплекс-методом.
Процедуры симплекс-метода позволяют установить, является ли задача линейного программирования разрешимой (невырожденной), и в этом случае найти оптимальное решение задачи за конечное число шагов.
Вычислительный алгоритм реализации модели ЛП симплекс-методом состоит из трёх этапов:
– сведение модели ЛП к каноническому виду;
– нахождение начального решения (опорного плана);
– нахождение оптимального решения (плана) методом симплекс-таблиц.
В 1947 году Дж. Данциг сформулировал общую задачу линейного программирования и метод ее решения - симплексный метод. Симплексный метод лежит в основе большинства других алгебраических методов решения задач линейного программирования. В силу этих причин изучение алгебраических методов решения задач линейного программирования начинается, как правило, именно с симплексного метода.
Начальное решение для реализации модели ЛП определяется после того, как задаваемые условия модели представлены в канонической форме.
Будем считать, что задача линейного программирования записана в стандартной форме. Пусть задача будет задачей максимизации целевой функции. Это, как известно, не является ограничением, поскольку задачу минимизации всегда можно преобразовать в равносильную задачу максимизации, поменяв знак перед целевой функцией на противоположный.
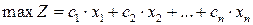 ,
,
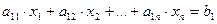 ,
,
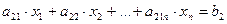 ,
,
……………………………………
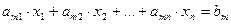 .
.
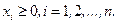
Будем считать также, что одно из базисных допустимых решений известно. Назовем это решение начальным.
Если система уравнений линейно независима, то любое ее базисное решение содержит m ненулевых базисных переменных. Пусть в начальном решении базисными являются последние m переменных из n: 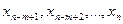 . Этого в любом случае можно добиться, перенумеровав переменные. Воспользовавшись методом исключений Гаусса, приведем систему к виду:
. Этого в любом случае можно добиться, перенумеровав переменные. Воспользовавшись методом исключений Гаусса, приведем систему к виду:
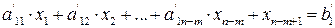 ,
,
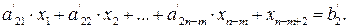
………………………………………………….
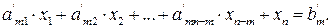
Поскольку решение, полученное с помощью базисных переменных 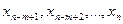 , является допустимым, то все
, является допустимым, то все 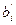 положительные величины. Выразим базисные переменные через небазисные:
положительные величины. Выразим базисные переменные через небазисные:
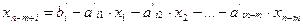 .
.
Подставив в целевую функцию вместо базисных переменных их значение из последнего соотношения, получим
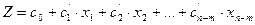
где: 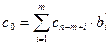 ,
, 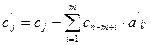 .
.
Положив все небазисные переменные равными нулю, получим начальное базисное решение 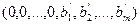 и значение целевой функции (линейной формы)
и значение целевой функции (линейной формы) 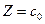 .
.
Анализ уравнения 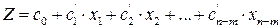 показывает, что целевую функцию можно максимизировать, увеличивая значения тех небазисных переменных, коэффициенты
показывает, что целевую функцию можно максимизировать, увеличивая значения тех небазисных переменных, коэффициенты 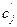 при которых больше нуля. Отсюда можно сформировать условие оптимальности решения задачи линейного программирования. Для задачи максимизации линейной формы, условие оптимальности формулируется следующим образом. Решение оптимально тогда и только тогда, когда для всех j имеет место неравенство
при которых больше нуля. Отсюда можно сформировать условие оптимальности решения задачи линейного программирования. Для задачи максимизации линейной формы, условие оптимальности формулируется следующим образом. Решение оптимально тогда и только тогда, когда для всех j имеет место неравенство 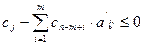 . Для задачи минимизации линейной формы это условие будет прямо противоположным: решение оптимально тогда и только тогда, когда для всех j имеет место неравенство
. Для задачи минимизации линейной формы это условие будет прямо противоположным: решение оптимально тогда и только тогда, когда для всех j имеет место неравенство 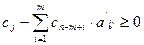 .
.
Увеличение небазисных переменных можно производить до тех пор, пока хоть одна из базисных переменных не окажется равной нулю. Увеличивать все небазисные переменные с положительными коэффициентами смысла нет, поскольку, в соответствии с теоремой об экстремуме линейной формы, оптимальное решение обязательно будет содержать n-m нулевых компонент вектора допустимых решений. Поэтому увеличивать начнем ту переменную, коэффициент в целевой функции при которой максимален. Назовем эту переменную переменной, вводимой в базис.
В принципе можно увеличивать и другую переменную. Важно чтобы соответствующий коэффициент был больше нуля. Но, как показывает опыт, первый вариант является более рациональным, требует для получения оптимального решения меньшее количество вычислений. Как следует из соотношений, при вводе выбранной переменной в базис и ее дальнейшем увеличении, значения переменных старого базиса также будут меняться. Пусть в базис вводится переменная 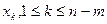 . Тогда для всех тех равенств, для которых
. Тогда для всех тех равенств, для которых  > 0, увеличение переменной
> 0, увеличение переменной 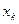 вызывает уменьшение базисной переменной
вызывает уменьшение базисной переменной 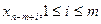 .
.
Но так как все переменные должны быть неотрицательными, поэтому увеличение переменной 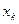 возможно до тех пор, пока первая из базисных переменных не окажется равной нулю. Назовем это условие условием допустимости. Пусть первой окажется равной нулю переменная
возможно до тех пор, пока первая из базисных переменных не окажется равной нулю. Назовем это условие условием допустимости. Пусть первой окажется равной нулю переменная  .
.
В результате описанной процедуры получены новый базис и новое значение целевой функции. Новый базис отличается от старого тем, что в нем переменная 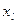 заменена на переменную
заменена на переменную 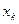 . Теперь вновь можно воспользоваться методом исключений Гаусса и получить систему уравнений. Описанный процесс необходимо повторять до тех пор, пока все коэффициенты целевой функции не окажутся отрицательными или равными нулю.
. Теперь вновь можно воспользоваться методом исключений Гаусса и получить систему уравнений. Описанный процесс необходимо повторять до тех пор, пока все коэффициенты целевой функции не окажутся отрицательными или равными нулю.
Подводя итоги, сформулируем алгоритм симплексного метода в виде следующих 4-х шагов:
1 .Отыскать допустимое начальное базисное решение. Если такого решения не существует, задача не имеет решения.
2. Преобразовать систему ограничений, а целевую функцию - к виду 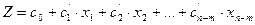 .
.
3. Воспользовавшись условием оптимальности определить, является ли текущее базисное решение оптимальным. Если да, то закончить вычисления. Если нет, то определить, какую переменную необходимо вводить в базис и перейти к п.4.
4. Воспользовавшись условием допустимости, определить какую переменную необходимо вывести из базиса и перейти к п.2.
Существует множество вариантов реализации данного алгоритма. Рассмотрим один из наиболее распространенных вариантов, получивший название табличного симплекс - метода. Для иллюстрации воспользуемся задачей о предприятии. Приведем стандартную форму данной задачи, несколько изменив форму записи целевой функции,
Максимизировать 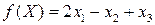 при ограничениях
при ограничениях
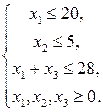
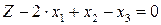 ,
,
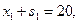
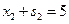
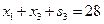 ,
,
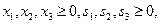
Нулевая итерация, шаг 1. Отыскать допустимое начальное базисное решение. Поскольку система ограничений содержит три линейных уравнения с шестью неизвестными, то любое ее базисное решение содержит три ненулевых компонент и три нулевые. Анализ ограничений показывает, что если переменным 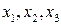 присвоить нулевое значение, получим допустимое (все переменные неотрицательны) базисное решение
присвоить нулевое значение, получим допустимое (все переменные неотрицательны) базисное решение 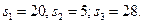 Запишем это решение в виде вектора (0,0,0,20,5,28).
Запишем это решение в виде вектора (0,0,0,20,5,28).
Шаг 2. Шаг 2 в данном конкретном случае исключается, поскольку исходная целевая функция не содержит базисных переменных, а ограничения уже записаны в требуемой форме.
Запишем целевую функцию и ограничения в табличной форме итерация 0. Эта таблица интерпретируется следующим образом.
Столбец "номер итераций" указывает количество итераций, выполненных в ходе решения задачи. В нем же могут указываться номера переменных, вводимых в базис и выводимых из базиса на данной итерации. Столбец "базисные переменные" содержит переменные текущего базиса. Значения этих переменных приведены в столбце "Решение". Подразумевается, что небазисные переменные (в данном случае 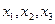 ) равны нулю. Значение целевой функции также равно нулю, что и показано в последней клетке Z-строки таблицы. В столбцах
) равны нулю. Значение целевой функции также равно нулю, что и показано в последней клетке Z-строки таблицы. В столбцах 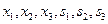 указаны коэффициенты при соответствующих переменных в целевой функции (строка Z) и в ограничениях (строки
указаны коэффициенты при соответствующих переменных в целевой функции (строка Z) и в ограничениях (строки 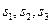 ).
).
Шаг 3. Как определить, является ли начальное решение оптимальным? Анализируя Z-строку симплекс-таблицы, нетрудно заметить, что небазисные переменные 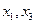 имеют отрицательные коэффициенты. Это эквивалентно наличию положительных коэффициентов в исходной целевой функции. Так как мы имеем дело с задачей максимизации, значит Z может быть увеличено при увеличении как
имеют отрицательные коэффициенты. Это эквивалентно наличию положительных коэффициентов в исходной целевой функции. Так как мы имеем дело с задачей максимизации, значит Z может быть увеличено при увеличении как 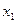 , так и
, так и  . Но поскольку коэффициент при переменной
. Но поскольку коэффициент при переменной 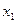 больше по модулю, чем коэффициент при переменной
больше по модулю, чем коэффициент при переменной  , именно ее целесообразно вводить в базис.
, именно ее целесообразно вводить в базис.
| Базис | x 1 | x 2 | x 3 | S 1 | S 2 | S3 | Решение |
| Z | -2 | -1 | |||||
| S1 | |||||||
| S2 | |||||||
| S3 |
Старая Z -строка: (-2 1 -1 0 0 0 | 0)
-(-2)´ s 1-строка: (1 0 0 1 0 0 | 20)
= Новая Z -строка: (0 1 -1 2 0 0 | 40)
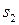 строка
строка
Старая 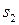 -строка: (0 1 0 0 1 0 | 5)
-строка: (0 1 0 0 1 0 | 5)
-(0)´ s 1-строка: (1 0 0 1 0 0 | 20)
= Новая 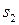 -строка: (0 1 0 0 1 0 | 5)
-строка: (0 1 0 0 1 0 | 5)
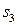 -строка
-строка
Старая 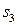 -строка: (1 0 1 0 0 1 | 28)
-строка: (1 0 1 0 0 1 | 28)
-(1)´ s 1-строка: (1 0 0 1 0 0 | 20)
= Новая 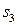 строка: (0 0 1 -1 0 1 | 8)
строка: (0 0 1 -1 0 1 | 8)
| Базис | x 1 | x 2 | x 3 | S 1 | S 2 | S3 | Решение |
| Z | -1 | ||||||
| x 1 | |||||||
| S2 | |||||||
| S3 | -1 |
Старая Z -строка: (0 1 -1 2 0 0 | 40)
-(-1)´ s3 -строка: (0 0 1 -1 0 1 | 8)
= Новая Z -строка: (0 1 0 1 0 1 | 48)
 строка
строка
Старая  -строка: (1 0 0 1 0 0 | 20)
-строка: (1 0 0 1 0 0 | 20)
-(0)´ s3 -строка: (1 0 0 1 0 0 | 20)
= Новая  -строка: (1 0 0 1 0 0 | 20)
-строка: (1 0 0 1 0 0 | 20)
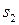 -строка
-строка
Старая 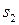 -строка: (0 1 0 0 1 0 | 5)
-строка: (0 1 0 0 1 0 | 5)
-(0)´ s 3-строка: (1 0 0 1 0 0 | 20)
= Новая 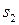 строка: (0 1 0 0 1 0 | 5)
строка: (0 1 0 0 1 0 | 5)
| Базис | x 1 | x 2 | x 3 | S 1 | S 2 | S3 | Решение |
| Z | |||||||
| x 1 | |||||||
| S2 | |||||||
| X 3 | -1 |
Ответ: 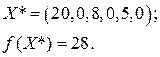
Метод М-штрафов
В теории линейного программирования разработаны два метода получения допустимого начального базисного решения задачи ЛП с помощью искусственных переменных: одноэтапный метод больших штрафов (М-метод) и двухэтапный метод искусственного базиса.
Наиболее распространен при нахождении начального решения метод искусственного базиса, заключающийся во введении искусственных переменных.
Начальное решение находится по следующим правилам.
Правило I. Если при сведении задачи ЛП к каноническому виду дополнительные переменные не вводились, либо все введенные дополнительные (избыточные) переменные вошли со знаком –, что возможно в трех случаях:
1) все ограничения первоначальной задачи ЛП заданы в виде уравнений;
2) все ограничения первоначальной задачи ЛП заданы в виде неравенств со знаком ³, причем 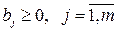 ;
;
3) часть ограничений задана неравенствами со знаком ³ (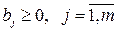 ), остальные ограничения – в виде равенств, то вводятся искусственные переменные (по числу линейных ограничений задачи)
), остальные ограничения – в виде равенств, то вводятся искусственные переменные (по числу линейных ограничений задачи) 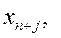
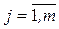 , (n – число переменных задачи ЛП, сформулированной в каноническом виде, m – число линейных ограничений), которые:
, (n – число переменных задачи ЛП, сформулированной в каноническом виде, m – число линейных ограничений), которые:
– с коэффициентами, равными единице, прибавляются к левым частям линейных уравнений искусственные переменные R:

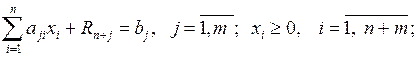
– с коэффициентами, равными М (где М – достаточно большое число), вводятся в целевую функцию в случае решения задачи минимизации
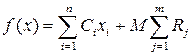 .
.
При решении задачи максимизации вводятся дополнительные элементы со знаком «-»
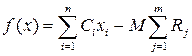 .
.
Таким образом, вводится «штраф» за дополнительно введенные искусственные переменные. Значение М выбирают заведомо большим. Поэтому при решении задачи оптимизации значение 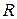 в конечном счете примет нулевое значение.
в конечном счете примет нулевое значение.
В качестве начального решения реализации модели выбирают
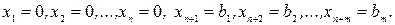
Переменные 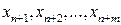 (
(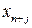 ,
, 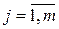 ) образуют начальный базис задачи и называются базисными.
) образуют начальный базис задачи и называются базисными.
Замечание. Искусственные величины, вводимые для создания искусственного базиса, не следует смешивать с дополнительными величинами, вводимыми при сведении задачи к каноническому виду и имеющими физический смысл.
Правило II. Если часть введенных дополнительных переменных вошла в уравнения со знаком +, т. е. часть ограничений исходной задачи была задана в виде неравенств со знаком £ (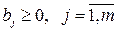 ), то количество искусственных переменных может быть уменьшено на число таких неравенств. Тогда в начальный базис, наравне с искусственными, войдут и дополнительные переменные.
), то количество искусственных переменных может быть уменьшено на число таких неравенств. Тогда в начальный базис, наравне с искусственными, войдут и дополнительные переменные.
Правило III. Если все введенные дополнительные переменные вошли в уравнения со знаком +, т.е. все ограничения первоначальной задачи были заданы в виде неравенств со знаком £ (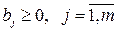 ), то в начальное решение (базис) войдут только дополнительные переменные. Введения искусственных переменных в этом случае не требуется.
), то в начальное решение (базис) войдут только дополнительные переменные. Введения искусственных переменных в этом случае не требуется.
Примеры. Модель ЛП задана в виде: найти переменные 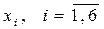 , обращающие целевую функцию
, обращающие целевую функцию 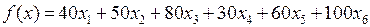 в минимум при следующих линейных ограничениях:
в минимум при следующих линейных ограничениях:
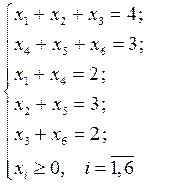 .
.
Построить начальный базис для её реализации.
Решение. Линейные ограничения записаны в виде равенств. Введем пять искусственных переменных: 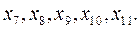
Модель ЛП примет следующий вид: найти переменные 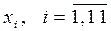 , обращающие целевую функцию
, обращающие целевую функцию
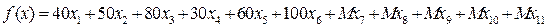 в минимум при следующих линейных ограничениях:
в минимум при следующих линейных ограничениях:
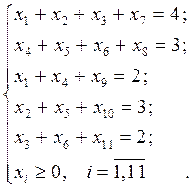
Приравняв все переменные, кроме искусственных, к нулю: 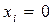 для всех
для всех 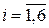 , получаем начальное решение задачи, удовлетворяющее всем линейным ограничениям:
, получаем начальное решение задачи, удовлетворяющее всем линейным ограничениям:
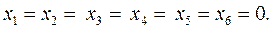
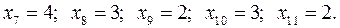
Ответ. Начальный базис для реализации модели ЛП:
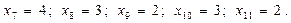
При этом 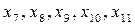 – базисные переменные;
– базисные переменные;
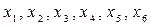 – небазисные (внебазисные) переменные.
– небазисные (внебазисные) переменные.
Для задачи переменные 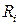 могут быть взяты за базисные. Можно показать, что если основная задача имеет решение, то соответствующая ей М -задача также имеет решение. Более того, оптимальный план М -задачи представляет собой вектор X, первые n компонент которого являются оптимальным планом решения основной задачи, а последние m компонент равны нулю. Если в оптимальном плане М задачи хоть одна из искусственных переменных отличается от нуля, основная задача оказывается неразрешимой.
могут быть взяты за базисные. Можно показать, что если основная задача имеет решение, то соответствующая ей М -задача также имеет решение. Более того, оптимальный план М -задачи представляет собой вектор X, первые n компонент которого являются оптимальным планом решения основной задачи, а последние m компонент равны нулю. Если в оптимальном плане М задачи хоть одна из искусственных переменных отличается от нуля, основная задача оказывается неразрешимой.
В качестве примера решим методом больших штрафов задачу. Формулировка М задачи требует введения искусственной переменной в каждое ограничение. Это оправдано при разработке программ для ЭВМ. При ручном счете целесообразно вводить искусственные переменные только в те ограничения, которые не содержат очевидных базисных переменных.
Рассмотрим задачу оптимизации
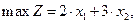
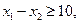
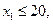
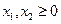
В нашей задаче не содержит очевидной базисной переменной первое ограничение, поэтому М задача формируется в виде
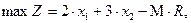
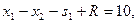
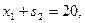
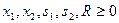 .
.
Решим эту задачу табличным симплекс-методом.
Первая итерация 1, шаг 1. Определим допустимое начальное базисное решение М задачи. В качестве начальных базисных переменных возьмем искусственную переменную R и остаточную переменную 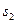 .
.
Шаг 2. Выразив R, 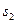 через небазисные переменные и подставив их в целевую функцию, получим
через небазисные переменные и подставив их в целевую функцию, получим
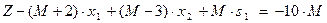
Теперь можно составить начальную симплекс-таблицу, итерация 0.
Шаг 3. Анализ начальной симплекс-таблицы показывает, что допустимое начальное базисное решение М-задачи оптимальным не является. Это следует из того, что коэффициент целевой функции при небазисной переменной 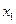 равный - (М+2) является отрицательным, так как по условию М-не определено большее число, а следовательно М>>2. Введению в базис подлежит
равный - (М+2) является отрицательным, так как по условию М-не определено большее число, а следовательно М>>2. Введению в базис подлежит 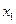 .
.
Шаг 4. Поскольку 10/1< 20/1, в соответствии с условием допустимости из базиса выведем переменную R. После чего начинаем новую итерацию.
Вторая итерация, шаг 2. Преобразуем строки начальной симплекс-таблицы в соответствии с формулами предыдущего параграфа. Результаты преобразований представлены в табл. итерация 1.
Шаг 3. Анализ симплекс-таблицы, полученной после преобразований показывает, что оптимальное решение М-задачи пока не найдено, и переменная  подлежит включению в базис.
подлежит включению в базис.
Шаг 4. Исключению из базиса подлежит переменная 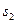 , поскольку именно для нее численное значение соотношения
, поскольку именно для нее численное значение соотношения 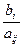 является минимальным.
является минимальным.
Таблица
| Номер итерации | Базисные переменные | Переменные | Решение | ||||
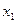
| 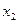
| 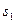
| 
| R | |||
| 0(начало вычислений) | Z | -(M+2) | (M-3) | М | -10M | ||
| R | - 1 | - 1 | |||||

| |||||||
| Z | - 5 | - 2 | M+2 | ||||
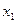
| - 1 | - 1 | |||||

| - 1 | ||||||
| 2 оптимум | Z | M-3 | |||||
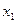
| |||||||
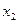
| - 1 |
Третья итерация, шаг 2. Преобразуем строки симплекс-таблицы, полученные в результате второй итерации, в соответствии с формулами предыдущего параграфа. Результаты преобразований отображены в нижней трети таблицы.
Шаг 3. Поскольку после преобразования все коэффициенты в Z -строке таблицы оказались больше или равными нулю, полученное решение является оптимальным.
Как следует из таблицы, оптимальным решением М-задачи является вектор X=(20,10,0,0,0), в котором искусственная переменная R оказалась равной нулю. Следовательно, первые две компоненты вектора оптимального решения М-задачи представляют собой оптимальный план решения исходной задачи, а величина линейной формы М задачи на ней равна величине линейной формы исходной задачи.
В заключение отметим, что если линейная форма основной задачи подлежит минимизации, то М задача формулируется в виде
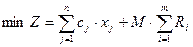 ,
,
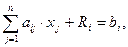
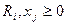 ,
,
i=1,..,m; j=1,..,n,
В остальном, различий между задачей максимизации и минимизации нет.
Метод больших штрафов целесообразно применять в тех задачах, у которых при стандартной форме записи число компонент вектора свободных переменных - n значительно превосходит число ограничивающих уравнений - m.
Не нашли, что искали? Воспользуйтесь поиском: