Спеціальні режими роботи сельсинів

У низці випадків використовують спеціальні режими роботи сельсинної системи синхронної передачі кута: робота одного датчика на кілька приймачів, передача при зсуві фази між напругами датчика та приймача, збільшена відстань між датчиком та приймачем, робота в системі синхронного зв’язку різнотипних датчика та приймача. Кожен з цих режимів має свої особливості, які ми розглянемо.

Досить часто в індикаторній системі синхронної передачі від одного датчика працює кілька приймачів, які забезпечують синхронний поворот або синхронне обертання індикаторів у кількох пунктах. Така передача застосовується, наприклад, при необхідності передачі положення якогось регулюючого органа на головний пульт керування та місцеві налагоджувальні пульти.

У відповідності з формулою (16.25)

, (16.66)

де z_д, z_п – відповідно опори датчика та приймача.

Тоді зі співвідношень (16.31):

. (16.67)

Синхронізуючий момент може бути розрахований за формулою (16.42) з урахуванням (16.44), (16.66), (16.67):

, (16.68)

. (16.69)

Питомий синхронізуючий момент дорівнює:

, (16.70)

де

. (16.71)

Якщо в схемі синхронної передачі використовуються два сельсина, то

;

. (16.72)

Якщо від одного датчика працює т однакових приймачів, то еквівалентний опір дорівнює:

. (16.73)

Тоді питомий синхронізуючий момент датчика:

. (16.74)

У зв’язку з тим, що через обмотки синхронізації кожного приймача проходить струм в т разів менший, ніж струм датчика, питомий синхронізуючий момент приймача буде в т разів меншим:

. (16.75)

Питомі синхронізуючі моменти датчика та приймача можливо виразити через М_сп2:

;

; (16.76)

; (16.77)

При т>1 М _{д сп} збільшується, а М_псп зменшується. Тому зменшується точність роботи системи. Для того, щоб зберегти точність синхронної передачі, необхідно, щоб

. (16.78)

Тоді з урахуванням формул (16.73), (16.74):

; (16.79)

. (16.80)

Таким чином, М_псп останеться без змін, а М _{д сп} зросте в т разів.

Для одержання високої точності необхідно, щоб усі приймачі мали однакову конструкцію, належали до одного класу точності й були однаково завантажені.

Стійкість приймачів у синхронному положенні збільшується зі збільшенням числа приймачів, оскільки на синхронізацію приймача діють і паралельно увімкнені приймачі.

При нерівномірному завантаженні приймачів створюється додатковий кут непогодження між приймачами, тобто похибка зростає.

Найбільша відстань між сельсинами визначається допустимим зменшенням синхронізуючого моменту, тобто опором лінії зв’язку. Визначимо, як залежить синхронізуючий момент М_с від опору лінії зв’язку. Для цього скористуємось формулами (16.49), (16.42), (16.20), (16.21):

, (16.81)

де

, (16.82)

β₂ визначається формулою (16.22), звідки:

; (16.83)

; (16.84)

; (16.85)

; (16.86)

. (16.87)

З урахуванням співвідношень (16.82)÷(16.87):

. (16.88)

Звичайно х>>х_лз, тобто δ_х≈0. З урахуванням цього:

. (16.89)

Якщо лінії зв’язку короткі, то можливо вважати δ_r≈0. Тоді:

. (16.90)

Зміну синхронізуючого моменту в залежності від r_лз можливо визначити, як

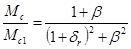. (16.91)

Зі співвідношення (16.91) видно, що відношення залежно від відносного активного опору ліній зв’язку δ_r за формулою (16.86) та від відносного індуктивного опору обмоток синхронізації β за формулою (16.84). При цьому β зростає зі збільшенням потужності сельсина.

Для підвищення далекості передачі зі збереженням М_с та інших рівних умов необхідно або зменшити δ_r, що пов’язане зі збільшенням перерізу провідників ліній зв’язку й тому не раціональне, або збільшити δ_х, вмикаючи в кожен промінь обмотки синхронізації дросель з опором х_др. В останньому випадку можливо не тільки зберегти М_с, але й підвищити його до М_стах.

Визначимо М_стах й величину х_др. Для цього визначимо з формули (16.81), при якому β_2кр виникає М_стах. Досліджуючи (16.81) на максимум, визначаємо що β_2кр=1. Тоді:

. (16.92)

Якщо в лінії зв’язку увімкнені дроселі, то у відповідності з (16.83)÷(16.87):

, (16.93)

де

, (16.94)

. (16.95)

З формули (16.92) з урахуванням (16.87):

. (16.96)

Зі співвідношення (16.81) з урахуванням (16.87):

. (16.97)

Відносне значення синхронізуючого моменту:

. (16.98)

Для визначення х_др скористаємось формулою (16.93) при β₂=β_2кр=1. Тоді:

. (16.99)

Отже, якщо параметри лінії зв’язку витримувати такими, щоб β₂=β_2кр=1, то далекість передачі можливо збільшити необмежено. З порушенням цієї умови М_с зменшується.

Збільшення далекості передачі може призвести до різних умов збудження датчика та приймача, напруга збудження датчика може виявитись більшою, ніж приймача. Тому послідовно з обмоткою збудження приймача вмикається обмотка трансформатора струму, яка додає величину ΔU, що пропорційна струмові навантаження.

З формули (16.44) визначається максимальний синхронізуючий момент М_стах.

Для одного променя датчика та приймача може бути наведена векторна діаграма рис.16.18, яка аналогічна рис.16.7.

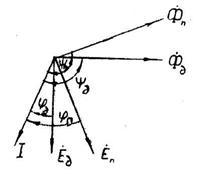
Рис. 16.18. Векторна діаграма сельсинної передачі при довгій живлячій мережі

З рис.16.18 витікає, що при довгій живлячій мережі, яка пов’язує обмотки збудження сельсинів, виникають різні фази напруг збудження та, відповідно, різні фази магнітних потоків Ф_зб та Ф_п. Тому виникає φ_п≠φ_д. Оскільки М_стах залежить від

,

тобто

; ,

то зі збільшенням індуктивності живлячої лінії

зростає φ_п, тобто напруга збудження приймача

буде випереджувати напругу збудження датчика

.

А це призведе до збільшення М_стах приймача, оскільки φ_п>φ_д.

В схемах синхронної передачі кута можуть застосовуватись різнотипні сельсини-датчики та сельсини-приймачі. Точність роботи таких систем буде оцінюватись за нижчим класом точності типа сельсина, застосованого в даній схемі. Кількість сельсинів-приймачів при багатократному прийманні в такому разі визначається експериментально.

Не нашли, что искали? Воспользуйтесь поиском: