I. Мера множества (площадь, объем).

ГЕОМЕТРИЧЕСКИЕ И МЕХАНИЧЕСКИЕ ПРИЛОЖЕНИЯ КРАТНЫХ ИНТЕГРАЛОВ.

I. Мера множества (площадь, объем).

Пусть 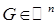, - измеримое 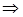(доказательство смотри раньше, приняв ):

при n=2 ;

при n=3 .

Для определенного интеграла:

а) Пусть - каноническая область I-го типа 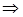(смотри ранее).

.

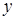
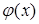
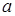
Аналогично для - каноническая область II-го типа:

.

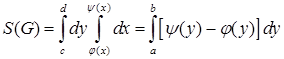б) Пусть 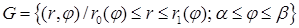- криволинейный сектор .

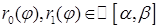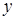
Тогда:

.

Если область охватывает начало координат:

.

б’) Объем цилиндрического тела.

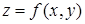
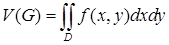
и однозначна.

в) Площадь поверхности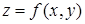

Если и имеет непрерывные частные производные в области 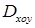, то:

1)

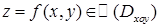
, где

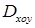- проекция на плоскость XOY.

2) :

, - проекция на плоскость XOZ.

3) :

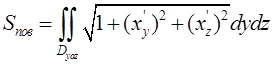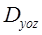, - проекция на плоскость YOZ.

4) Случай неявного задания поверхности: .

Площадь , заданной уравнением выражается интегралом:

5) Случай параметрического задания поверхности.

Если уравнение поверхности задано параметрически:

, где , - ограниченная область, в которой функции непрерывно-дифференцируемы, то:

где 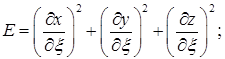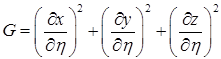и

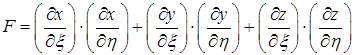. Е, G, F – коэффициенты Гаусса

ЗАМЕЧАНИЕ.

Площадь поверхности в полярных координатах:

.

6) Пусть - тело с заданной площадью поперечного сечения.

.

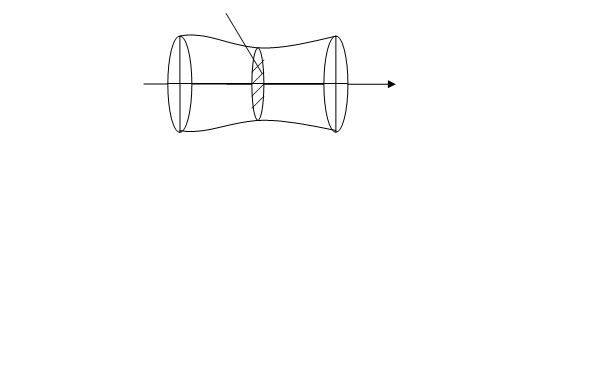
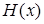
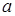
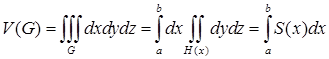7) Пусть - тело, полученное вращением криволинейной трапеции вокруг оси OX.

.

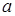
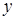
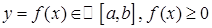Из 6 следует, что .

8) Объем - цилиндроида (см. ранее).

.

Не нашли, что искали? Воспользуйтесь поиском: