КРИВОЛИНЕЙНЫЙ ИНТЕГРЛ 1-ГО РОДА.

Df.1 Пусть , 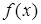- определена в , . Совокупность области и функции 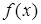называется скалярным полем. - вектор.

При n=2, 3 под понимают - радиус-вектор. Тогда имеем скалярную функцию векторного аргумента:

.

Если точка , являющаяся концом радиуса-вектора , то можно писать . Если (при n=3) 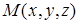или , то пишут 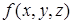. Понятие криволинейного интеграла непосредственно связано с понятием кривой.

Кривой в 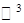называется 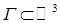, являющаяся непрерывным отображением:

.

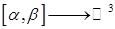Задается векторной функцией скалярного аргумента (1)

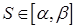- параметр. Как известно (1) эквивалентно:

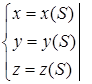(2)

.

A – начало, B – конец кривой. Если - замкнутая.

Задать направление обхода задать начало и конец.

Следует отметить, что для криволинейных интегралов 1-го рода определение , теоремы существования, теоремы о среднем, свойства и т.д. были изложены раньше.

Не нашли, что искали? Воспользуйтесь поиском: