
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Функциональные ряды. Степенные ряды. Ряд Маклорена
Определение 1. Бесконечная сумма функций u 1(x) + u 2(x) +…+ un (x) +…, где un (x) = f (x,n), называется функциональным рядом.
Если задать конкретное числовое значение х, ряд превратится в числовой ряд, причем в зависимости от выбора значения х такой ряд может сходиться или расходиться. Практическую ценность представляют только сходящиеся ряды, поэтому важно определить те значения х, при которых функциональный ряд становится сходящимся числовым рядом.
Определение 2. Множество значений х, при подстановке которых в функциональный ряд получается сходящийся числовой ряд, называется областью сходимости функционального ряда.
Определение 3. Функция s(x), определенная в области сходимости ряда, которая для каждого значения х из области сходимости равна сумме соответствующего числового ряда, полученного при данном значении х, называется суммой функционального ряда.
Пример. Найдем область сходимости и сумму функционального ряда
1 + х + х ² +…+ xn +…
При | x | ≥ 1 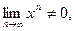 поэтому соответствующие числовые ряды расходятся. Если же | x | < 1, рассматриваемый ряд представляет собой сумму бесконечно убывающей геометрической прогрессии, вычисляемую по формуле:
поэтому соответствующие числовые ряды расходятся. Если же | x | < 1, рассматриваемый ряд представляет собой сумму бесконечно убывающей геометрической прогрессии, вычисляемую по формуле:
 .
.
Следовательно, областью сходимости ряда является интервал (-1, 1), а его сумма имеет указанный вид.
Замечание. Так же, как для числовых рядов, можно ввести понятия частичной суммы функционального ряда:
sn = 1 + х + х ² +…+ xn
и остатка ряда: rn = s – sn.
Не нашли, что искали? Воспользуйтесь поиском: