б) матричный метод (с помощью обратной матрицы).

Решение.

Чтобы исследовать совместность системы – воспользуемся теоремой Кронекера – Капелли и найдем ранги расширенной матрицы системы и матрицы системы.

Найдем ранг матрицы методом элементарных преобразований. Ранг матрицы равен числу ненулевых строк в матрице после приведения её к ступенчатой форме при помощи элементарных преобразований над строками матрицы.

Так как ранги данных матриц равны, система совместна и имеет единственное решение.

Метод Крамера

Найдем определитель системы

Δ=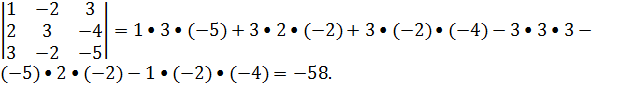

Так как определитель матрицы системы Δ =-58≠0, то система совместна и имеет единственное решение.

Заменим первый столбец матрицы А на столбец свободных членов:

Δ₁=

Заменим второй столбец матрицы А на столбец свободных членов:

Δ₂=

Заменим третий столбец матрицы А на столбец свободных членов:

Δ=

по формулам Крамера:

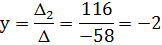
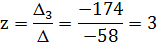
б) матричный метод (с помощью обратной матрицы).

Данную систему запишем в матричной форме и решим с помощью обратной матрицы.

Пусть А – матрица коэффициентов при неизвестных; X – матрица-столбец неизвестных x,y,z и Н – матрица-столбец из свободных членов:

, ,

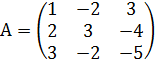Левую часть системы (1) можно записать в виде произведения матриц , а правую в виде матрицы Н. Следовательно имеем матричное уравнение

. (2)

Так как определитель матрицы А отличен от нуля:

Δ=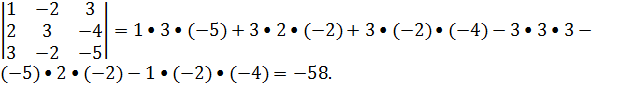

то матрица А имеет обратную матрицу .

Умножим обе части равенства (2) слева на матрицу , получим

.

Так как , где Е – единичная матрица, а , то

. (3)

Пусть имеем невырожденную матрицу А:

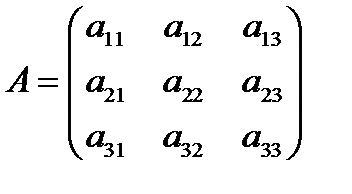
Тогда обратную матрицу находим по формуле:

где A_ij — алгебраическое дополнение элемента a_ij в определителе матрицы А, которое является произведением (-1)^i+j на минор (определитель) n-1 порядка, полученный вычеркиванием i-й строки и j-го столбца в определителе матрицы А:

,

- ,

=1

,

=2∙-2-3∙3=-13,

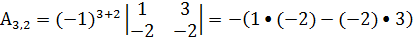=-4,

Отсюда получаем обратную матрицу:

=

Находим столбец неизвестных X: X=A^-1 • H.

Ответ:

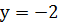
Метод Гаусса.

Приведем расширенную матрицу системы к ступенчатому виду

Последняя матрица эквивалентна системе уравнений:

Выполняем обратный ход метода Гаусса:

из второго уравнения системы: , и из первого уравнения системы .

Ответ:

Не нашли, что искали? Воспользуйтесь поиском: