ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ

Основные понятия о математических моделях на основе дифференциальных уравнений

Законы Вселенной написаны на языке математики. Алгебра решает много задач с постоянными величинами, но самые интересные природные явления включают изменение и описываются уравнениями, которые связывают изменяющиеся величины. Поскольку производная dx/dt = f′(t) функции f является скоростью изменения величины х = f(t), которая зависит от независимой переменной t, естественно, что уравнения, содержащие производные, часто используются для описания изменений, происходящих во Вселенной. Уравнение, связывающее неизвестную функцию и одну или несколько ее производных, называют дифференциальным уравнением

Пример:

Предположим, что — численность колонии бактерий в момент времени t. Численность колонии в момент времени t = 0 была равна 1000 и что количество бактерий удваивается через каждый час. Эта дополнительная информация о P(t) приводит к следующим уравнениям:

1000 = Р(0) = Ce0 = C, 2000 = Р(1) = Cek

Из этого следует, что С = 1000 и что = 2, так что k = ln 2 ≈ 0.693147. При этом значении k дифференциальное уравнение принимает следующий вид: =(ln 2)P≈ 0.693147P, замена k = ln 2 и С = 1000 в дает частное решение P(t) = 1000 = 1000⋅ (так как =2), которое удовлетворяет указанным условиям. Можно использовать это частное решение, чтобы предсказать численность колонии бактерий в будущем. Например, предсказанная численность бактерий после полутора часов (t = 1.5) равна: Р(1.5) = 1000 • ≈ 2828. Условие Р(0) = 1000 в примере 6 называют начальным условием, потому что часто пишут дифференциальные уравнения, для которых t = 0 является "временем пуска". На рис. 1.3 показано несколько различных графиков функции вида P(t) = С 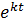при k = ln 2. Графики всего бесконечного множества решений = kР фактически заполняют всю двумерную плоскость, и никакие два из них не пересекаются. Кроме того, выбор любой точки P0 на оси P определяет Р(0). Поскольку через каждую такую точку проходит только одно решение, то мы видим, что начальное условие Р(0)=P0 определяет единственное решение, согласующееся с имеющимися данными.

Текст на MATLAB

k=log(2);

t=-1:0.5:5;

C=[ -0.12; -0.06; -0.03; -0.01; -0.005; 0.005; 0.01; 0.03; 0.06; 0.12]; P=C*exp(k*t);

plot(t,P);

title('P(t)=C*e^k^*^t');

xlabel('t');

ylabel('P(t)');

text(3.1,2.78, 'P(t)= 0.12*e^k^*^t\rightarrow');

text(3.45,1.78, 'P(t)= 0.06*e^k^*^t\rightarrow');

text(3.2,0.85, 'P(t)= 0.03*e^k^*^t\rightarrow');

text(3.1,-0.78, 'P(t)= -0.03*e^k^*^t\rightarrow');

text(3.45,-1.78, 'P(t)= -0.06*e^k^*^t\rightarrow');

text(3.1,-2.78, 'P(t)= -0.12*e^k^*^t\rightarrow');

grid on

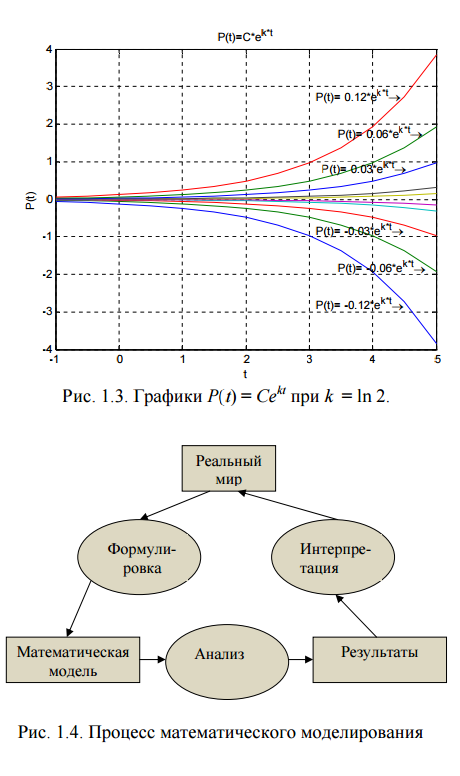
Краткое обсуждение прироста населения в примерах 1.5 и 1.6 иллюстрирует процесс математического моделирования (рис. 1.4), который включает следующие этапы.

ЗАКЛЮЧЕНИЕ

Математическое моделирование - более универсальный метод, чем физическое. Изменение параметров моделируемой системы или аппарата не требует трудоемких переделок модели.

Хорошо построенная модель, как правило, доступнее, информативнее и удобнее для исследования, нежели реальный объект.

Таким образом поставленные мною цели и задачи были достигнуты. Я изучил теоретические вопросы математического моделирования, его этапы, классификацию моделей. Разобрал примеры математического моделирования на задачах " об охлаждении тела" и «о радиоактивном распаде» и научился использовать методы математического моделирования при исследовании различных природных социальных процессов.

СПИСОК ЛИТЕРАТУРЫ

1. Самарский А. А., Михайлов А. П. Математическое моделирование: Идеи. Методы. Примеры. — 2-е изд., испр. — М.: Физматлит, 2001. —320 с.

2. Овсянников Л. В. Групповой анализ дифференциальных уравнений. М.: Наука, 1978. — 400 с.

3. Шубин М. А. «Математический анализ для решения физических задач» МЦНМО, 2003

4. Вабищевич П.Н. «Математическое моделирование». — М.: Изд-во МГУ, 1993. — 152 с.

5. Бочков М.В., Ловачев Л.А., Четверушкин Б.Н. Химическая кинетика образования NO при горении метана в воздухе // Математическое моделирование. — 1992. — Т. 4, № 9. — С. 3-36.

6. Арсенъев А.А., Самарский А.А. Что такое математическая физика. — М.: Знание, 1983. — 64 с.

7. А. Г. Коробейников Разработка и анализ математических моделей с использованием MATLAB и MAPLE:(Санкт-Петербург 2010).

Не нашли, что искали? Воспользуйтесь поиском: