Дифференциальное исчисление функций нескольких переменных.

1. Последовательность точек в .Теорема о покоординатной сходимости. Следствие об ограниченной последовательности.

2. Предел функции р переменных. Непрерывность функции р переменных. Теорема Вейерштрасса.

3. Повторные пределы функции двух переменных. Примеры. Условие совпадения повторных и двойных пределов.

4. Дифференцируемость функции р переменных. Дифференцируемость суммы и произведения дифференцируемых функций.

5. Частные производные функции р переменных. Связь между дифференцируемостью функции и существованием частных производных. Пример функции, которая имеет частные производные в точке А, но не дифференцируема в этой точке.

6. Дифференцируемость функции в случае существования и непрерывности частных производных.

7. Производная сложной функции. Частные производные сложной функции. Инвариантность формы первого дифференциала.

8. Частные производные высших порядков. Теорема о равенстве смешанных производных.

9. Дифференциалы высших порядков. Отсутствие инвариантности формы у дифференциалов порядка выше первого.

10. Формула Тейлора функции р переменных.

11. Теорема о существовании и дифференцируемости неявно заданной функции одной переменной. Вычисление первой и второй производных функции у(х), заданной неявно уравнением

12. Теорема о существовании и дифференцируемости неявно заданных функций р переменных, заданных системой функциональных уравнений. Приемы вычисления производных. Вычисление первых и вторых производных функции z(x,y), заданной неявно уравнением

.

Вычисление первых производных функций y(x), z(x), u(x), заданных неявно системой

.

13. Определение точек экстремума функции нескольких переменных. Необходимые и достаточные условия существования точек экстремума.

14. Определение точек условного экстремума функции нескольких переменных. Необходимые и достаточные условия существования точек условного экстремума. Пример: найти точки условного экстремума функции при условии .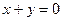

Не нашли, что искали? Воспользуйтесь поиском: