
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
ЗАДАЧИ ДЛЯ КОНТРОЛЬНОЙ РАБОТЫ. 1-10.Найти пределы, не пользуясь правилом Лопиталя.
1-10. Найти пределы, не пользуясь правилом Лопиталя.
1. а)  ; б)
; б)  ; в)
; в)  ;
;
г)  ; д)
; д)  ; е)
; е) 
2. а) 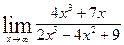 ; б)
; б)  ; в)
; в)  ;
;
г)  ; д)
; д)  ; е)
; е) 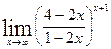 .
.
3. а)  ; б)
; б) 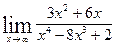 ; в)
; в)  ;
;
г)  ; д)
; д) 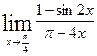 ; е)
; е)  .
.
4. а) 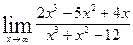 ; б)
; б)  ; в)
; в)  ;
;
г)  ; д)
; д)  ; е)
; е)  .
.
5. а)  ; б)
; б)  ; в)
; в)  ;
;
г) 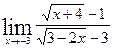 ; д)
; д)  ; е)
; е)  .
.
6. а)  ; б)
; б)  ; в)
; в)  ;
;
г)  ; д)
; д) 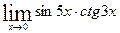 ; е)
; е) 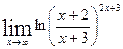 .
.
7. а)  ; б)
; б) 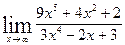 ; в)
; в)  ;
;
г) 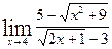 ; д)
; д)  ; е)
; е)  .
.
8. а) 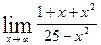 ; б)
; б)  ; в)
; в)  ;
;
г)  ; д)
; д)  ; е)
; е)  .
.
9. а)  ; б)
; б)  ; в)
; в)  ;
;
г) 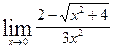 ; д)
; д)  ; e)
; e) 
10. а)  ; б)
; б)  ; в)
; в)  ;
;
г) 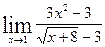 ; д)
; д) 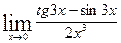 ; е)
; е)  .
.
11-20. Исследовать функцию на непрерывность в указанных точках.
11.  ; х1 = 1, х2 = 2.
; х1 = 1, х2 = 2.
12.  ; х1 = 2, х2 = 3.
; х1 = 2, х2 = 3.
13.  ; х1 = 2, х2 = 4.
; х1 = 2, х2 = 4.
14.  ; х1 = - 2, х2 = -1.
; х1 = - 2, х2 = -1.
15.  ; х1 = -3, х2 = -2.
; х1 = -3, х2 = -2.
16. 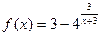 ; х1 = -3, х2 = -2.
; х1 = -3, х2 = -2.
17.  ; х1 = 2, х2 = 4.
; х1 = 2, х2 = 4.
18.  ; х1 = 1, х2 = 2.
; х1 = 1, х2 = 2.
19.  ; х1 = -5, х2 = -4.
; х1 = -5, х2 = -4.
20. 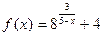 ; х1 = 4, х2 = 5.
; х1 = 4, х2 = 5.
21-30. Исследовать на непрерывность функцию, найти точки разрыва, указать характер разрыва и построить график функции y = f (x) в области определения.
 – 2x + 1 при –2 £ x£ –1,
– 2x + 1 при –2 £ x£ –1,
21. f(x) =  при –1 < x £ 1,
при –1 < x £ 1,
2x при 1 < x £ 2.
 |
–x 2 при –2 £ x£ –1,
22. f(x) =  при –1 < x £ 1,
при –1 < x £ 1,
3x–1 при 1 < x £ 2.
 2 x 2 при –2 £ x£ 0,
2 x 2 при –2 £ x£ 0,
23. f(x) = 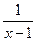 при 0 < x £ 2,
при 0 < x £ 2,
1 при 2 < x £ 3.
 –x –2 при –2 £ x£ –1,
–x –2 при –2 £ x£ –1,
24. f(x) = 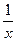 при –1 < x £ 1,
при –1 < x £ 1,
ln x при 1 < x £ e.
 –x 2 при –2 £ x£ –1,
–x 2 при –2 £ x£ –1,
25. f(x) = 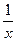 при –1 < x £
при –1 < x £  ,
,
2 sin x  при
при  < x £
< x £  .
.
 – x– 2 при –3 £ x£ –1,
– x– 2 при –3 £ x£ –1,
26. f(x) = 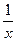 при –1 < x £ 2,
при –1 < x £ 2,
1 при 2 < x £ 3.

 при –1 £ x£ 0,
при –1 £ x£ 0,
27. f(x) =  при 0 < x £ 1,
при 0 < x £ 1,
 при 1 < x £ 3.
при 1 < x £ 3.

 при –2 £ x£ 0,
при –2 £ x£ 0,
2 8. f(x) = 2x2–1 4 при 0 < x£ 1,
1 при 1 < x £ 3.
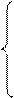 2x2 –1 при –1 £ x£ 0,
2x2 –1 при –1 £ x£ 0,
29. f(x) =  при 0 < x£ 2,
при 0 < x£ 2,
x–1 при 2 < x£ 3.
 cos x при –
cos x при –  £ x< 0,
£ x< 0,
30. f(x) =  при 0 < x £ 2,
при 0 < x £ 2,
x + 1 при 2 < x£ 3.
31 - 40. Найти производные  данных функций.
данных функций.
31. а)  ; б)
; б)  ;
;
в) 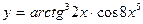 ; г)
; г)  .
.
32. а)  ; б)
; б)  ;
;
в)  ; г)
; г) 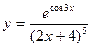 .
.
33. а)  ; б)
; б) 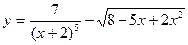 ;
;
в)  ; г)
; г)  .
.
34. а)  ; б)
; б) 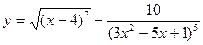 ;
;
в)  ; г)
; г)  .
.
35. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
36. а)  ; б)
; б)  ;
;
в) 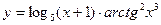 ; г)
; г)  .
.
37. а) 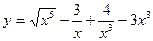 ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
38. а)  ; б)
; б)  ;
;
в) 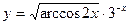 ; г)
; г) 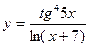 .
.
39. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
40. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
41-50. Найти  и
и  для заданных функций и вычислить их значения в данной точке х0.
для заданных функций и вычислить их значения в данной точке х0.
41.  , х0 = 0.
, х0 = 0.
42. у = sin2x, x0 = p/2.
43. y = ln(2 + x2), x0 = 0.
44. y = x4 lnx, x0 = 1.
45. y = e xsin2x, x0 = 0.
46. y = x sinx, x0 = p/2.
47. y = (x+1) ln(x+1), x0 = -1/2.
48. y = ln3x, x0 = 1.
49. y = e- x cosx, x0 = 0.
50. y = x 2 lnx, x0 = 1/3.
51-60. Найти дифференциалы первого и второго порядка для заданных функций и вычислить их значения в заданной точке х0.
51. 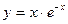 , х0 = 0.
, х0 = 0.
52.  , х0 =1.
, х0 =1.
53.  , х0 = 0.
, х0 = 0.
54. 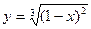 , х0 = 2.
, х0 = 2.
55.  , х0 =1.
, х0 =1.
56. 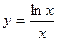 , х0 = 1.
, х0 = 1.
57.  , х0 = -1.
, х0 = -1.
58. 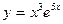 , х0 = 0.
, х0 = 0.
59.  , х0 = -1.
, х0 = -1.
60. 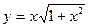 , х0 = 0.
, х0 = 0.
61-70. С помощью дифференциала вычислить приближенное значение данной величины.
61.  . 62. tg460.
. 62. tg460.
63.  . 64. arctg1,05.
. 64. arctg1,05.
65.  . 66. cos590.
. 66. cos590.
67. e2,01. 68. ctg440.
69. lg11. 7 0. sin1510.
71. Проверитьсправедливость теоремы Ролля для функции y =  на данном отрезке [–2;2]. Найти соответствующее значение с (если оно существует).
на данном отрезке [–2;2]. Найти соответствующее значение с (если оно существует).
72. Найти точку, в которой касательная к кривой y = x2 – 4x параллельно хорде, соединяющей точки А (1, –3) и В (5,5). Сделать поясняющий рисунок.
73. Проверить справедливость теоремы Лагранжа для функции y=еx на данном отрезке [0,1]. Найти соответствующее значение с (если оно существует).
74. Дана функция y =  . Пусть а = 0, b = 16. Тогда y(0) = y (16) = 4. Однако производная этой функции не обращается в нуль ни в одной точке интервала (0,16). Противоречит ли это теореме Ролля?
. Пусть а = 0, b = 16. Тогда y(0) = y (16) = 4. Однако производная этой функции не обращается в нуль ни в одной точке интервала (0,16). Противоречит ли это теореме Ролля?
75. Проверитьсправедливость теоремы Ролля для функции y = –x2 + 4x –3 на данном отрезке [0,4]. Найти соответствующее значение с (если оно существует).
76. Найти точку, в которой касательная к кривой y = ln x параллельно хорде, соединяющей точки А (1, 0) и В (е,1). Сделать поясняющий рисунок.
77. Проверить справедливость теоремы Лагранжа для функции y =  на данном отрезке [0,3]. Найти соответствующее значение с (если оно существует).
на данном отрезке [0,3]. Найти соответствующее значение с (если оно существует).
78. Проверитьсправедливость теоремы Ролля для функции y =  на данном отрезке [-1,1]. Найти соответствующее значение с (если оно существует).
на данном отрезке [-1,1]. Найти соответствующее значение с (если оно существует).
79. Проверить справедливость теоремы Лагранжа для функции y= 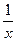 на данном отрезке [
на данном отрезке [ 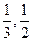 ]. Найти соответствующее значение с (если оно существует).
]. Найти соответствующее значение с (если оно существует).
80. Проверитьсправедливость теоремы Ролля для функции y = cosx на данном отрезке [  ]. Найти соответствующее значение с (если оно существует).
]. Найти соответствующее значение с (если оно существует).
81-90. Найти пределы, используя правило Лопиталя.
81.  . 86.
. 86.  .
.
82.  . 87.
. 87.  .
.
83. 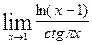 . 88.
. 88. 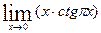 .
.
84.  . 89.
. 89.  .
.
85. 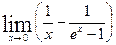 . 90.
. 90. 
91.-100. Исследовать методами дифференциального исчисления функции  и, используя результаты исследования, построить их графики.
и, используя результаты исследования, построить их графики.
91. а) 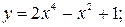 б)
б) 
92. а)  б)
б) 
93. а)  б)
б) 
94. а)  б)
б) 
95. а)  б)
б) 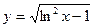
96. а)  б)
б) 
97. а)  б)
б) 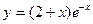
98. а)  б)
б) 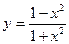
99. а)  б)
б) 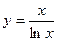
100. а)  б)
б) 
101-110. Найти частные производные функции  .
.
101.  . 106.
. 106.  .
.
102.  . 107.
. 107.  .
.
103.  . 108.
. 108. 
104.  . 109.
. 109. 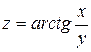 .
.
105.  . 110.
. 110. 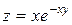 .
.
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ.
Не нашли, что искали? Воспользуйтесь поиском: