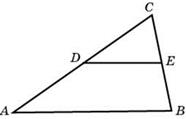
Площадь треугольника равна 4. — средняя линия. Найдите площадь треугольника CDE

Часть1

1. Си­сте­ма на­ви­га­ции, встро­ен­ная в спин­ку са­мо­лет­но­го крес­ла, ин­фор­ми­ру­ет пас­са­жи­ра о том, что полет про­хо­дит на вы­со­те 37 170 футов. Вы­ра­зи­те вы­со­ту по­ле­та в мет­рах. Счи­тай­те, что 1 фут равен 30,5 см.

2. На диаграмме показано распределение выплавки алюминия в 10 странах (в тысячах тонн) за 2009 год. Среди представленных стран первое место
по выплавке алюминия занимал Бахрейн, десятое место — Новая Зеландия. Какое место занимали Нидерланды?

3. Найдите площадь трапеции, изображенной на рисунке.

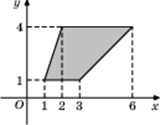
4. В чем­пи­о­на­те по гим­на­сти­ке участ­ву­ют 25 спортс­ме­нок: 12 из Рос­сии, 7 из Укра­и­ны, осталь­ные — из Бе­ло­рус­сии. По­ря­док, в ко­то­ром вы­сту­па­ют гим­наст­ки, опре­де­ля­ет­ся жре­би­ем. Най­ди­те ве­ро­ят­ность того, что спортс­мен­ка, вы­сту­па­ю­щая пер­вой, ока­жет­ся из Бе­ло­рус­сии.

5. Найдите корень уравнения .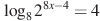

Площадь треугольника равна 4. — средняя линия. Найдите площадь треугольника CDE

7. На ри­сун­ке изоб­ражён гра­фик про­из­вод­ной y = f' (x) функ­ции y = f (x), опре­делённой на ин­тер­ва­ле (−4; 8). В какой точке от­рез­ка [−3; 1] функ­ция y = f (x) при­ни­ма­ет наи­мень­шее зна­че­ние?

8. Объем куба равен 8. Най­ди­те пло­щадь его по­верх­но­сти.

Часть 2

9. Найдите значение выражения .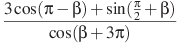

10. Некоторая компания продает свою продукцию по цене 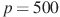руб. за единицу, переменные затраты на производство одной единицы продукции составляют 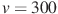руб., постоянные расходы предприятия руб. в месяц. Месячная операционная прибыль предприятия (в рублях) вычисляется по формуле 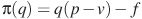. Определите месячный объём производства (единиц продукции), при котором месячная операционная прибыль предприятия будет равна 300000 руб.

11. Рас­сто­я­ние между го­ро­да­ми A и B равно 440 км. Из го­ро­да A в город B со ско­ро­стью 50 км/ч вы­ехал пер­вый ав­то­мо­биль, а через час после этого нав­стре­чу ему из го­ро­да B вы­ехал со ско­ро­стью 80 км/ч вто­рой ав­то­мо­биль. На каком рас­сто­я­нии от го­ро­да A ав­то­мо­би­ли встре­тят­ся? Ответ дайте в ки­ло­мет­рах.

12. Най­ди­те наи­боль­шее зна­че­ние функ­ции 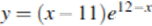на от­рез­ке .

13. а) Решить уравнение 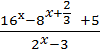= 5.

б) Найти все корни этого уравнения, принадлежащие отрезку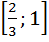

14. Косинусугла между боковой гранью и основанием правильной треугольной пирамиды равен . Найти угол между двумя боковыми гранями пирамиды с общим боковым ребром.

15. Решить неравенство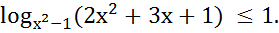

16. В остроугольном треугольнике АВС провели высоту ВН. Из точки Н на стороны АВ и АС опустили перпендикуляры НК и НМ соответственно.

а) Докажите, что треугольник МВК подобен треугольнику АВС.

б) Найдите отношение площади треугольника МВК к площади четырехугольника АКМС, если ВН = 3, а радиус окружности, описанной около треугольника АВС, равен 4.

17. Строительство нового завода стоит 75 млн. рублей. Затраты на производство х тыс. ед. продукции на таком заводе равны 0,5 х²+х+7 млн. рублей в год. Если продукцию завода продавать по цене p тыс. рублей за единицу, то прибыль фирмы (в млн. рублей) за один год составит p x – (0,5x²+x+7). Когда завод будет построен, фирма будет выпускать продукцию в таком количестве, чтобы прибыль была наибольшей. При каком наименьшем значении p строительство завода окупится не более чем за 3 года?

18. Найти все значения а, при которых уравнение

((а – 1) х² + 3х)² – 2((а -1)х² + 3х) + 1 – а ² = 0

имеет ровно два решения.

19. Про некоторый набор, состоящий из 11 различных натуральных чисел, известно, что сумма любых двух различных чисел этого набора меньше суммы любых трех различных чисел этого набора.

а) Может ли одним из этих чисел быть число 3000?

б) Может ли одним из этих чисел быть число16?

в) какое наименьшее возможное значение может принимать сумма такого набора?

Не нашли, что искали? Воспользуйтесь поиском: