
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Описание объекта управления. Математическая модель объекта получается на основе законов Кирхгофа и имеет вид дифференциального уравнения
Математическая модель объекта получается на основе законов Кирхгофа и имеет вид дифференциального уравнения
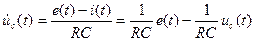
 (1)
(1)
где x(t)=uc(t), u(t)=e(t), p, b – числа, равные p = -1/RC, b = 1/RC
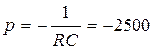 ,
,  .
.
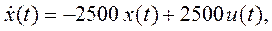
1.2. Конструирование функционала – критерия оптимальности.
Найдем выражение для суммарной энергии активных потерь в схеме за время t1–t0. Оно представляется в виде
 . (2)
. (2)
Для этого записываем выражение для активной мощности потерь на сопротивлениях r и R:

или,

Получим, что q =1/R = 0,0125, n = -2/R = - 0,025, m = 1/r + 1/R = 0,1458.
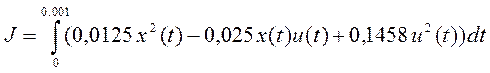
1.3. Формулировка задачи как вариационной задачи на условный экстремум.
Для этого необходимо рассматривать в качестве уравнения связей уравнение системы (1), а в качестве функционала – функционал (2).
Таким образом, получаем следующую вариационную задачу:
Определить функции x(t) и u(t), доставляющие экстремум функционалу
 ,
,
при граничных условиях  ,
,

и при дополнительном условии (уравнении связи)
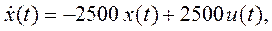
накладываемом на функции x(t), u(t), в классе которых ищется экстремум.
1.4. Синтез оптимального алгоритма управления.
1.4.1. Получение уравнений вариационной задачи.
Уравнения Эйлера – Лагранжа имеют вид
 ,
,  ,
,
в которых


l(t) – неопределенный множитель Лагранжа, Φ – функция Лагранжа.
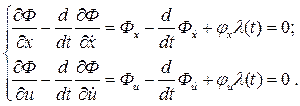
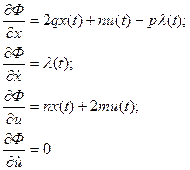
В итоге получаем систему уравнений:

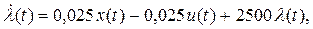 (3)
(3)
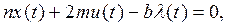
 (4)
(4)

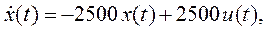 (5)
(5)
Здесь (3), (4) – уравнения Эйлера – Лагранжа. К этим уравнениям добавлено уравнение объекта (5) (уравнение связи).
1.4.2. Отыскание решения уравнений вариационной задачи.
Решим уравнения (3) – (5) в следующем порядке:
1) Выразим из (4) u(t):

Затем подставим его в (3) и (5).


При этом получается система уравнений
 ,
, 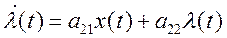
с коэффициентами
a11 = p – nb/2m = -2285,67,
a12 = b2/2m = 2,1433*107,
a21 = 2q – n2/2m = 0,022,
a22 = nb/2m – p = 2285,67.
Таким образом получим следующую систему:

 (6)
(6)
2) Запишем систему (6) в матричной форме
 , (7)
, (7)
где
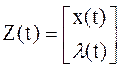 ,
,

 .
.
3) Запишем решение уравнения (7) в виде
 , (8)
, (8)
где
 – вектор начальных условий, а матричная экспонента
– вектор начальных условий, а матричная экспонента  определяется по формуле Лагранжа – Сильвестра
определяется по формуле Лагранжа – Сильвестра
 ,
,
где l1, l2 – собственные числа матрицы А. Е - единичная матрица.
Собственные числа матрицы А определяются из условия  . Таким образом получим
. Таким образом получим
 ,
,
 .
.

Для определения неизвестного начального значения множителя Лагранжа l(t0), входящего в (8)
а) запишем (8) для момента времени t1
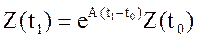
или
 ,
,
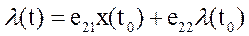 , (9)
, (9)
где e11, е12, е21, е22 – элементы матрицы (числа):
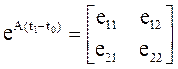

б) определим l(t0) из первого уравнения системы (9)

Таким образом 
Решим уравнение (7):

4). Запишем выражения для оптимальной траектории и оптимального управления:
 - оптимальная траектория
- оптимальная траектория
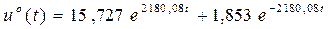 - оптимальное управление
- оптимальное управление
Не нашли, что искали? Воспользуйтесь поиском: