Описание объекта управления. По закону Кирхгофа для узла 1 имеем:

По закону Кирхгофа для узла 1 имеем:

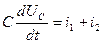или (1)

Рассмотрим контуры I и II. По закону Кирхгофа для напряжений получаем:

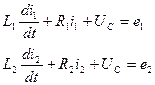(2)

Введем обозначения:

, , .

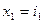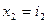Тогда выражения (1), (2) можно записать в виде:

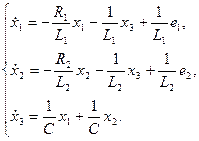
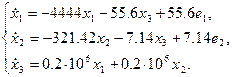(3)

Уравнения для выходных переменных

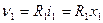, . (4)

Объединяя (3) и (4), получаем математическую модель электрической схемы:

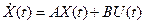(5)

где

, , ,

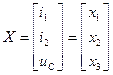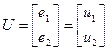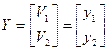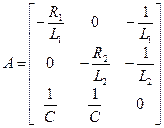, , С= ,

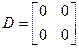
Подставляя числовые значения параметров, получим:

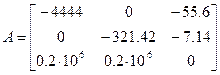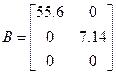, , С= ,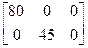

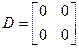
Начальное положение объекта: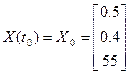

Конечное положение объекта: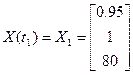

2.2. Конструирование функционала – критерия оптимальности

Критерий оптимальности – квадратичный функционал

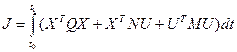 (6)

где 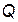- симметричная, неотрицательно-определенная матрица чисел, размерами 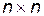; 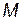- симметричная, положительно-определенная матрица чисел размерами .

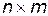Введем обозначения:

,

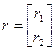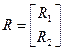
Запишем выражение для активной мощности по­терь на конденсаторе С, сопротивлениях r₁, r₂ и R₁, R₂:

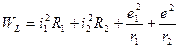
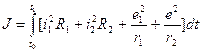
Таким образом,

,

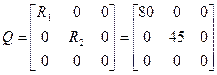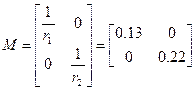
2.3. Формулировка задачи как вариационной задачи на услов­ный экстремум.

Для этого необходимо рассматривать в качестве уравнения связей уравнение системы (1), а в качестве функционала – функционал (2).

Таким образом, получаем следующую вариационную задачу:

Определить функции x(t) и u(t) доставляющие экстремум функционалу

,

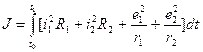при граничных условиях

,

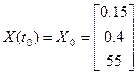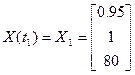
и при дополнительных условиях (уравнениях связи)

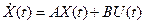
накладываемом на функции x(t), u(t), в классе которых ищется экстремум.

Не нашли, что искали? Воспользуйтесь поиском: