
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Реализация метода средней точки в пакете Mathcad
ДОКЛАД
Численные методы оптимизации. Метод средней точки
Руководитель ___________ А. П. Прокопьев
подпись, дата
Студент СФ 15-07М 411514790 ___________ А. С. Шулбаева
подпись, дата
Красноярск 2016
Численные методы
При решении указанных задач редко удается воспользоваться аналитическими методами, так как аналитические решения возможны лишь в редких случаях при решении инженерных задач, когда оптимизируемые функции представлены в аналитической форме. Кроме того, математические модели часто задаются не в виде формул, а с помощью оператора и нахождения значений функций f (x 1, x 2,..., xn) осуществляют алгоритмически, путем вычисления по некоторому алгоритму.
Сущность метода
Предположим, что на отрезке [a,b] нужно найти минимум непрерывно дифференцируемой и унимодальной функции f(x).
Пусть x1 - середина отрезка [a,b], т.е. x1=(a+b)/2.
Находим K = f ‘(x1) - значение производной целевой функции в середине отрезка [a,b].
Если K>0 то, переходим к отрезку [a, x1].
Если K<0 то переходим к отрезку [x1, b].
На каждом шаге длина отрезка, содержащего точку экстремума, уменьшается в два раза. Этим данный метод напоминает метод дихотомии, но метод средней точки эффективнее.
Условием прекращения вычислений может быть либо достаточно малая длина полученного отрезка, либо достаточно малое значение абсолютной величины производной.
Реализация метода средней точки в пакете Mathcad
| Задание: найти максимум целевой функции с помощью метода средней точки. |


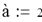

Построим график функции для того чтобы убедиться что функция непрерывна на этом интервале, и на этом интервале расположена одна точка экстремума.

Задачи поиска максимума эквивалентны задачам поиска минимума, так как требуется лишь поменять знак перед функцией.

| Найдем производную данной функции |





СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
1. Методы оптимизации в примерах в пакете MathCAD 15. Ч. I: Учеб. пособие / И.В. Кудрявцева, С.А. Рыков, С.В. Рыков, Е.Д. Скобов. – СПб.: НИУ ИТМО, ИХиБТ, 2014. – 166 с.
2. Пантелеев А.В., Летова Т.А. Методы оптимизации в примерах и задачах: Учеб. пособие. 2-е изд., испр. – М.: Высш. шк., 2005. – 544 с.
| <== предыдущая лекция | | | следующая лекция ==> |
| ЭМОЦИОНАЛЬНЫЕ ПОРТРЕТЫ | | | Фонд оценочных средств по дисциплине |
Не нашли, что искали? Воспользуйтесь поиском: