
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Пример решения задачи вычисления определенного интеграла с использованием пакета Excel
Решение.
Аналитическое вычисление данного интеграла дает I = агсtg(1)–агсtg(0) = = 0,7853981634. В нашем случае:
1)h = 1; xо = 0; x1 = 1;
2) h = 0,25 (1/4); x0 = 0; x1 = 0,25; x2 = 0,5; х3 = 0,75; x4 = 1; 
Вычислим методом левых прямоугольников:
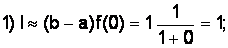

Вычислим методом правых прямоугольников:
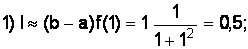
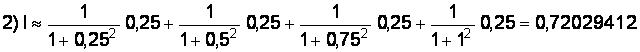
Вычислим методом средних прямоугольников:
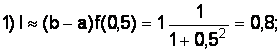

Вычислим методом трапеций:
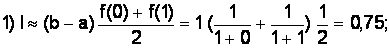

4.4. Метод Симпсона (парабол)
Этот метод базируется на замене подынтегральной функции квадратичной параболой, которая строится уже не по двум (как прямая в методе трапеций), а по трем точкам на каждом участке (поэтому число разбиений должно быть четным). По этим трем точкам (крайние точки участка и средняя точка) строится интерполяционная функция – полином второго порядка, который аналитически интегрируется [2]. Получается следующая расчетная формула:
• для одного участка интегрирования:
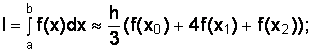 (4.18)
(4.18)
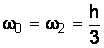 ; (4.19)
; (4.19)
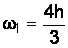 , (4.20)
, (4.20)
где x0 = a; x1 = (b–a)/2; x2 = b; h = (b–a)/2;
• для n участков интегрирования:
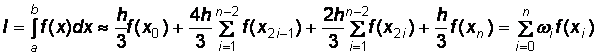 ; (4.21)
; (4.21)
 (4.22)
(4.22)
 ; (4.23)
; (4.23)
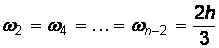 . (4.24)
. (4.24)
В формуле (4.24) все ординаты с нечетными номерами имеют коэффициент 4h/З, а с четными – 2h/3 (кроме нулевого и последнего). При работе с этим методом обязательно разбивают весь интервал на четное число участков.
На рис. 4.6 приведен пример вычисления интеграла методом Симпсона. По сравнению с методами прямоугольников и трапеций он более точен, что наглядно видно из графика (подынтегральная функция почти совпадает с параболой).
 Метод Симпсона обеспечивает вычисление интеграла точно, без погрешности при полиноме третьего порядка. Следовательно, этот метод предпочтительнее предыдущих. Количественно оценить погрешность при использовании двойного просчета можно по соотношению
Метод Симпсона обеспечивает вычисление интеграла точно, без погрешности при полиноме третьего порядка. Следовательно, этот метод предпочтительнее предыдущих. Количественно оценить погрешность при использовании двойного просчета можно по соотношению
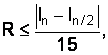 (4.25)
(4.25)
т. е. при увеличении числа разбиений в 2 раза погрешность падает в 15 раз.
Теоретические формулы оценки погрешности содержат производную четвертого порядка от подынтегральной функции, поэтому не имеют практического значения [2].
Пример
Рассмотрим вычисление интеграла из предыдущего раздела.
Решение
В случае одного участка будем иметь: x0 = 0, x1 = 0,5, х2 = 1, h = 0,5.

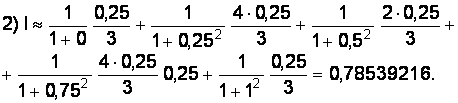
Пример решения задачи вычисления определенного интеграла с использованием пакета Excel
Постановка задачи. Задан определенный интеграл 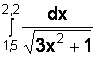 .
.
Определить приближенное значение интеграла методами прямоугольников, трапеций и Симпсона (парабол). Проинтегрировать аналитически и определить относительную погрешность вычислений.
Выполнение. Необходимо занести исходные данные в ячейки электронной таблицы:
| a = | 1,5 | |
| b = | 2,2 | |
| n = | ||
| h = | (2,2 – 1,5) / 20 = | 0,035. |
Вычислить точное значение определенного интеграла по формуле Ньютона–Лейбница.
Точное значение интеграла F(x)=  = 0,210529.
= 0,210529.
F(a) = 0,65456866; F(b) = 0,86509805; F(b)–F(a) = 0,210529.
Подготовить табл. 4.1 с данными, необходимыми для расчета определенного интеграла различными методами.
Таблица 4.1
Не нашли, что искали? Воспользуйтесь поиском: