
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Расчет интеграла различными методами
| I | x | y | x+h/2 | f(x+h/2) |
| 1,5 | 0,359211 | 1,518 | 0,355595 | |
| 1,535 | 0,352046 | 1,553 | 0,348562 | |
| 1,57 | 0,345142 | 1,588 | 0,341784 | |
| 1,605 | 0,338486 | 1,623 | 0,335247 | |
| 1,64 | 0,332067 | 1,658 | 0,328942 | |
| 1,675 | 0,325872 | 1,693 | 0,322855 | |
| 1,71 | 0,319891 | 1,728 | 0,316977 | |
| 1,745 | 0,314113 | 1,763 | 0,311298 | |
| 1,78 | 0,30853 | 1,798 | 0,305809 | |
| 1,815 | 0,303132 | 1,833 | 0,300500 | |
| 1,85 | 0,297911 | 1,868 | 0,295364 | |
| 1,885 | 0,292858 | 1,903 | 0,290392 | |
| 1,92 | 0,287966 | 1,938 | 0,285578 | |
| 1,955 | 0,283227 | 1,973 | 0,280914 | |
| 1,99 | 0,278636 | 2,008 | 0,276393 | |
| 2,025 | 0,274185 | 2,043 | 0,272010 | |
| 2,06 | 0,269868 | 2,078 | 0,267759 | |
| 2,095 | 0,265681 | 2,113 | 0,263633 | |
| 2,13 | 0,261616 | 2,148 | 0,259628 | |
| 2,165 | 0,25767 | 2,183 | 0,255739 | |
| 2,2 | 0,253837 |
Выполнить вычисление определенного интеграла по расчетным формулам для различных методов и найти относительную погрешность каждого метода.
Метод прямоугольников
Левых
Формула расчета:  .
.
Значение интеграла 0,212383711.
Относительная погрешность 0,88079 %.
Правых
Формула расчета: 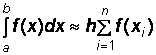 .
.
Значение интеграла 0,208695619.
Относительная погрешность 0,87103 %.
Средних
Формула расчета: 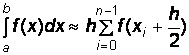 .
.
Значение интеграла 0,210524257.
Относительная погрешность 0,00244 %.
Метод трапеций
Формула расчета:
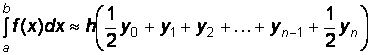 .
.
Значение интеграла 0,210539665.
Относительная погрешность 0,00488 %.
Метод Симпсона
Формула расчета:
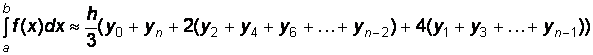 .
.
Значение интеграла 0,210529395.
Относительная погрешность 0 %.
ЛАБОРАТОРНАЯ РАБОТА № 7 ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ
Цель работы: изучить разные методы вычисления определенных интегралов.
Задание
Вычислить определенный интеграл по формулам прямоугольников, трапеций и Симпсона с четырьмя знаками после запятой. Определить относительную погрешность для каждого метода.
ВАРИАНТЫ
Вариант № 1
1)  2)
2) 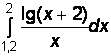
Вариант № 2
1)  2)
2) 
Вариант № 3
1) 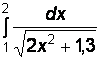 2)
2) 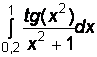
Вариант № 4
1)  2)
2) 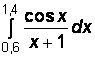
Вариант № 5
1)  2)
2) 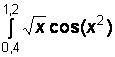
Вариант № 6
1)  2)
2) 
Вариант № 7
1)  2)
2) 
Вариант № 8
1) 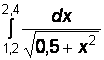 2)
2) 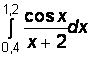
Вариант № 9
1) 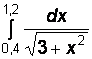 2)
2) 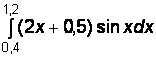
Вариант № 10
1) 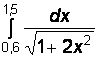 2)
2) 
Вариант № 11
1) 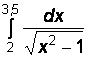 2)
2) 
Вариант № 1
1)  2)
2) 
Вариант № 13
1) 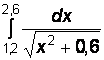 2)
2) 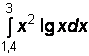
Вариант № 14
1)  2)
2) 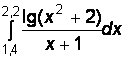
Вариант № 15
1) 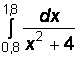 2)
2) 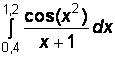
Вариант № 16
1) 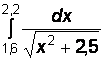 2)
2) 
Вариант №1 7
1) 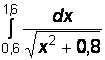 2)
2) 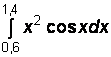
Вариант № 18
1) 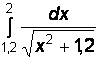 2)
2) 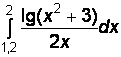
Вариант № 19
1) 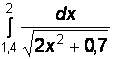 2)
2) 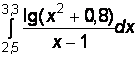
Вариант № 20
1) 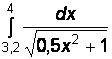 2)
2) 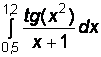
Вариант № 21
1) 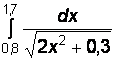 2)
2) 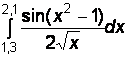
Вариант № 22
1) 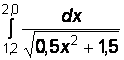 2)
2) 
Вариант № 23
1)  2)
2) 
Вариант № 24
1)  2)
2) 
Вариант № 25
1) 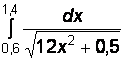 2)
2) 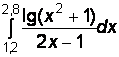
Вариант № 26
1) 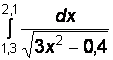 2)
2) 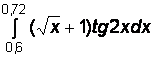
Вариант № 27
1) 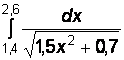 2)
2) 
Вариант № 28
1) 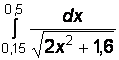 2)
2) 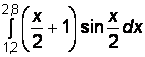
Вариант № 29
1) 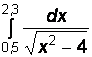 2)
2) 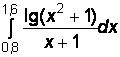
Вариант № 30
1)  2)
2) 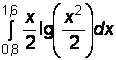
Не нашли, что искали? Воспользуйтесь поиском: