
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
IV.4.1 Теоретические основы применения электрохимических методов исследования коррозии
Электрохимические методы могут быть использованы только для исследования коррозионных процессов, протекающих по электрохимическому механизму. Химическая коррозия (процесс окисления металла и восстановления окислителя), протекает в одном акте, например:
n Me + m Ox → MenOxm, (IV.6)
Me – металл, Ox – окислитель (например кислород), Me n Ox m – соединение металла с окислителем (например оксид), n,m – стехиометрические коэффициенты.
В случае электрохимической коррозии, окислительный (анодный) и восстановительный (катодный) процессы пространственно разделены. Такая ситуация возможна лишь в тех случаях, когда корродирующий металл контактирует с электропроводной коррозионной средой, то есть, коррозионная среда должна представлять собой раствор электролита. Если для случаев, например, морской коррозии, контакт металла с электропроводной коррозионной средой (H2O+NaCl) очевиден, то в случаях атмосферной коррозии (даже если атмосфера не содержит агрессивных компонентов (Cl2, SO2 и пр.)), на поверхности металла возможно образование пленки конденсата, в котором будет растворено некоторое количество углекислого газа, присутствующего в атмосфере. Образующаяся в этой пленке угольная кислота, будет диссоциировать с образованием ионов Н+ и HCO3- и все равно раствор, контактирующий с металлом, окажется электропроводным. В случае электрохимической коррозии, при контакте конкретного атома металла с частицей - окислителем совершенно необязательна реализация процесса восстановления. То же самое справедливо в отношении анодного процесса, то есть, для окисления атома металла до состояния катиона нет необходимости в контакте этого атома с частицей – окислителем. Таким образом, электрохимическая коррозия является совокупностью двух независимых процессов, анодного и катодного, например:
Me → Me n + + n e- (IV.7а)
Ox + n e- → Red n -, (IV.7б)
где Me n + - катион метала, Red n - - продукт восстановления окислителя, n -количество электронов перенесенных через границу раздела металл - коррозионная среда при окислении атома металла или при восстановлении частицы окислителя.
Из сказанного можно вывести следующее.
Во-первых, для окисления грамм-атома металла, равно как и для восстановления моля окислителя, необходимо, что бы через границу раздела металл - коррозионная среда прошел заряд Q = n. Na . qe, где Na= 6,022141·1023 моль−1 - число Авогадро, qe = −1,602176565·10−19 Кл - заряд электрона. Перемножение qe и Na дает постоянную Фарадея F = Na.qe= 96485,3 Кл/моль. Применительно к коррозионному процессу известный первый закон электролиза М. Фарадея можно записать как
M= Q.Am / F .n, (IV.8)
где M – масса окисленного металла или масса потребленного в коррозионном процессе окислителя, Am – соответственно атомная масса металла или молярная масса окислителя. Поэтому как скорость коррозионного процесса в целом, так и скорости катодного и анодного процессов по отдельности можно выразить через плотность электрического тока, переносимого через границу раздела металл - коррозионная среда:
icorr = Q/(t.S), (IV.9)
где S – площадь поверхности корродирующего металла, а t - время коррозионного процесса.
Во-вторых, для течения анодного процесса (IV.7а) не имеет значения природа окислителя в катодном процессе (IV.7б), важно лишь соблюдение равенства n в анодном и катодном процессах. Поэтому потребление электронов в процессе (IV.7б) совершенно правомерно заменить отводом электронов от металла с помощью источника электрического тока. То же самое относится и к процессу (IV.7а), только вместо отвода электронов от металла с помощью источника электрического тока требуется их подача на металл. Следовательно, электрохимически можно исследовать анодный или катодный процессы по отдельности, отводя или подавая электроны, то есть, пропуская через металл анодный или катодный токи.
Как следует из (IV.7а,б), анодный и катодный процессы коррозии, протекающей по электрохимическому механизму, связаны с переносом заряда через границу раздела металл – коррозионная среда. Если при этом на межфазной границе существует электрическое поле, то работа по переносу заряженных частиц в этом поле будет вносить определенный вклад в течение коррозионного процесса.
В общем случае коррозионная система представляет собой совокупность двух (или более) многокомпонентных фаз. В простейшем случае это фаза металла (компоненты – катионы металла и электроны), находящаяся в контакте раствором, включающем молекулы воды, катионы металла и анионы. Чтобы охарактеризовать энергию частиц одного сорта принадлежащей одной фазе (например, катионов металла, находящихся в коррозионной среде или тех же катионов, принадлежащих кристаллической решетке металла), следует прибегнуть к понятию «химический потенциал». Химический потенциал (mi) это термодинамическая функция, применяемая при описании состояния систем с переменным числом частиц. В случае системы, состоящей из i компонентов, химический потенциал определяется как приращение внутренней энергии U системы при добавлении к системе бесконечно малого количества молей i- го компонента, отнесённое к этому количеству вещества, при постоянных объёме V, энтропии S и количествах молей каждого из остальных компонентов nj (j ¹ i). В общем случае химический потенциал может быть определён как приращение любого из остальных термодинамических потенциалов системы при различных постоянных параметрах: гиббсовой энергии G — при постоянных давлении Р, температуре Т и nj; гельмгольцевой энергии А — при постоянных V, Т и nj; энтальпии Н — при постоянных S, р и nj. Таким образом:


 (IV.10)
(IV.10)
Химический потенциал зависит от концентрации данного компонента, и от температуры:
mi = mi 0+ R T ln ai, (IV.11)
где ai - активность i- го компонента, а mi 0 – стандартный химический потенциал компонента, т.е. химический потенциал при температуре T = 298оK и
ai = 1, R – универсальная газовая постоянная.
Энергия частицы находящейся в одной фазе в общем случае отличается от энергии этой частицы принадлежащей другой фазе. Поэтому при приведении в контакт металла и коррозионной среды компоненты, обладающие в фазе большим химическим потенциалом, будут переходить в фазу, в которой их химический потенциал меньше. Поскольку среди компонентов обязательно есть заряженные частицы, то каждая фаза приобретет равные по величине, но противоположные по знаку электрические заряды, а между фазами возникнет разность потенциалов. Для учета электрических взаимодействий компонентов в электрохимических (и в частности коррозионных) системах вводят понятие электрохимического потенциала.
Электрохимический потенциал mEi помимо химической работы учитывает работу по переносу заряженных частиц через межфазную границу.
mEi = mi + n F φ = mi 0+ RT ln ai + n F φ, (IV.12)
где φ – внутренний потенциал – работа переноса единичного положительного точечного заряда из бесконечности в вакууме в фазу. Работа перемещения заряженной частицы из металла в коррозионную среду (раствор) определяется разностью электрохимических потенциалов этой частицы в металле и в растворе. В процессе переноса заряженных частиц из одной фазы в другую, ее активность в одной из фаз будет возрастать, а в другой, соответственно снижаться. Поэтому значения mEi в фазах согласно (IV.12) будут сближаться и в конечном итоге сравняются. При этом скорость переноса частиц сорта i из металла в раствор сравняется со скоростью переноса этих частиц в противоположном направлении. При этом частицы сорта i в обеих фазах приходят в состояние равновесия.
Равенство электрохимических потенциалов заряженной частицы в обеих фазах является условием равновесия при переходе ее через межфазную границу:
(mEi)металл = (mEi)раствор. (IV.13)
Подставляя значения электрохимических потенциалов частицы i из (IV.12) в (IV.13) получаем равновесное значение разности внутренних потенциалов металла и раствора, т.е. равновесное значение скачка потенциала между этими фазами:
 , (IV.14)
, (IV.14)
где  .
.
Определить значение скачка потенциала между металлом и раствором экспериментально невозможно. Это можно пояснить следующим образом. Допустим, что необходимо измерить значение скачка потенциала между медным образцом и контактирующим с ним раствором сульфата меди. Для этого нужно подключить первую клемму вольтметра к медному образцу, а провод, соединенный со второй клеммой погрузить в раствор. При этом вольтметр измерит разность потенциалов (напряжение) между медным образцом и проводом. В случае если провод медный, измеряемое напряжение будет равно нулю, в случае, если провод будет изготовлен из другого металла, то вольтметр покажет разность скачков потенциалов на границах медь/раствор и металл провода/раствор. Поскольку значение последнего скачка потенциала неизвестно, то неизвестно и искомое значение скачка потенциала. Проблема решается следующим образом (рис. IV.11). Вторую клемму подключают к сосуду, в которую помещают дополнительную систему металл/раствор, находящуюся в равновесии. Раствор, находящийся в сосуде приводят в электрический контакт с испытуемым раствором посредством, так называемого электролитического ключа – трубки, заполненной раствором, концы которой закрыты пористым материалом. Поскольку концентрация раствора в сосуде остается неизменной, то и скачок потенциала в этой системе также будет неизменен (IV.14). Таким образом, будет измерено значение:
E=(φ)металл-(φ)раствор - Const, (IV.15)
называемое электродным потенциалом. Const - скачок потенциала металл/ раствор в нашей дополнительной электродной системе, которую называют электродом сравнения.
Если исследуемая электродная система находится в равновесии, можно рассчитать равновесное значение электродного потенциала.
 (IV.16)
(IV.16)
Это - так называемое уравнение Нернста, записанное для системы, в которой лишь одна частица может переноситься через межфазную границу. Если таких частиц несколько, то в числителе и знаменателе выражения под логарифмом будут произведения активностей соответствующих частиц.
 |
Для системы металл – раствор, содержащий ионы данного металла уравнение Нернста можно записать следующим образом:
 (IV.17)
(IV.17)
Подставляя в (IV.16) значение F и переходя от натурального логарифма к десятичному логарифму, и учитывая, что aMe = 1, получаем:
 , (IV.17а)
, (IV.17а)
откуда следует, что при n = 1, при повышении активности ионов металла в растворе в 10 раз равновесный потенциал системы увеличивается на 0,059 В.
Поскольку абсолютное значение межфазного скачка потенциала экспериментально определить нельзя, условно принято, что стандартный равновесный потенциал системы (Pt/H+,H2) EH2 = 0. В этой системе платина выступает в роли инертного металла – не вступает в реакции. На поверхности платинового электрода протекают катодная реакция восстановления катионов водорода и анодная реакция окисления водорода:
2H+ + 2e ↔ H2. (IV.18)
Рассмотренная система называется водородным электродом (рис. IV.12), а при соблюдении стандартных условий: активность катионов водорода a H+=1г-ион/л, давление водорода P H2=1 атм, абсолютная температура
Т=298 oK – стандартным водородным электродом.
Стандартные значения равновесных электрохимических реакция рассчитывают из термодинамических данных, для ряда реакций эти значения приведены в таблице (IV.1)
Скорость коррозионного процесса (IV.7а,б) в стационарном режиме определяется скоростью наиболее медленной реакции (анодной или катодной). Действительно, если например, наиболее медленной является реакция
(IV.7б), то в результате реакции (IV.7а) на металле в единицу времени не может образоваться больше электронов, чем отводится от металла в результате реакции (IV.7б). То же справедливо в отношении реакции (IV.7б), если наиболее медленной является реакция (IV.7а). Наиболее медленная электрохимическая реакция, определяющая скорость коррозионного процесса называется лимитирующей. Например, при коррозии железа в нейтральных водных средах, коррозионный процесс можно представить следующим образом:
Fe → Fe2+ + 2e (IV.19а)
½ O2 + H2O + 2e → 2OH- (IV.19б)
Таблица IV.1 Стандартные электродные потенциалы
| Реакция | Потенциал, В | Реакция | Потенциал, В |
| K+ +e ↔ K | -2,925 | Рb2+ + 2е ↔ РB | -0,126 |
| Ва2+ + 2е ↔Ва | -2,900 | Fe3+ + Зе ↔ Fe | -0,037 |
| Mg2+ + 2е ↔Mg | -2,370 | Н+ + е ↔1/2Н2 | 0,000 |
| А13+ + Зе ↔ А1 | -1,660 | Sn4+ + 4е ↔Sn | +0,007 |
| Ti2+ + 2е ↔Ti | -1,630 | Bi3+ + Зе ↔ Bi | +0,215 |
| Ti3+ -b Зе ↔ Ti | -1,210 | Sb3+ + Зе ↔ Sb | +0,240 |
| Мn2+ + 2е ↔ Мn | -1,180 | Cu2+ + 2е ↔Сu | +0,337 |
| Сг2+ + 2е ↔ Сг | -0,913 | Со3+ + Зе ↔Со | +0,418 |
| Zn2+ + 2е ↔ Zn | -0,762 | Сu+ + е ↔ Сu | +0,521 |
| Сг3+ + Зе ↔* Сг | -0,740 | Ag+ + е ↔Ag | +0,799 |
| Fe2+ + 2e <=* Fe | -0,440 | Hg2+ + 2e ↔Hg | +0,854 |
| Cd2+ + 2е ↔Cd | -0,402 | Pd2+ + 2e ↔* Pd | +0,987 |
| Мn3+ + Зе ↔ Мn | -0,283 | Ir3+ + 3e ↔ Ir | +1,150 |
| Со2+ + 2е ↔ Со | -0,277 | Pt2+ + 2e ↔ Pt | +1,190 |
| Ni2+ + 2е ↔Ni | -0,250 | Au3+ + Зе ↔ Аu | +1,500 |
| Мо3+ + Зе ↔± Мо | -0,200 | Au+ + e ↔ Аu | +1,690 |
| Sn2+ + 2е ↔ Sn | -0,136 |
В большинстве случаев медленной является реакция (IV.19б) и ее скорость ограничена скоростью диффузии растворенных молекул кислорода к поверхности металла. В таких случаях принято говорить, что процесс протекает при диффузионном контроле. При коррозии железа в кислых средах коррозионный процесс можно представить как
Fe → Fe2+ + 2e (IV.20а)
2Н+ + 2e → H2 (IV.20б)
Наиболее вероятно, в этом случае медленной является реакция (IV.20б) и скорость коррозионного процесса определяется скоростью межфазного переноса заряда. В таких случаях говорят, что процесс протекает при кинетическом контроле.
В общем случае скорость электрохимического процесса (а, следовательно, и коррозионного процесса, протекающего по электрохимическому механизму) зависит от электродного потенциала.
В ходе любого гетерогенного процесса (химического, электрохимического) вблизи межфазной границы изменяются концентрации реагирующих компонентов – уменьшаются концентрации исходных веществ, возрастают концентрации продуктов реакции. В результате возникает разность концентраций компонентов реакции в зоне фазы прилегающей к межфазной границе и в зоне, достаточно от нее удаленной.
 Это приводит к диффузии компонента реакции из удаленной зоны к межфазной границе. В результате формируется зона, в которой концентрация определенного вещества вблизи межфазной границы (поверхностная концентрация Cs) отличается от его концентрации в зоне, находящейся на достаточном удалении от межфазной границы (объемная концентрация Cv). В любой точке этой зоны скорость диффузионного переноса вещества в направлении нормальном к межфазной границе определяется соотношением (первый закон Фика):
Это приводит к диффузии компонента реакции из удаленной зоны к межфазной границе. В результате формируется зона, в которой концентрация определенного вещества вблизи межфазной границы (поверхностная концентрация Cs) отличается от его концентрации в зоне, находящейся на достаточном удалении от межфазной границы (объемная концентрация Cv). В любой точке этой зоны скорость диффузионного переноса вещества в направлении нормальном к межфазной границе определяется соотношением (первый закон Фика):
 , (IV.21)
, (IV.21)
где J - плотность потока вещества (количество молей вещества, приносимое в единицу времени в направлении координаты x через поверхность площадью в единицу расположенную нормально к координате x) D –коэффициент диффузии 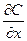 - градиенту концентрации. Это уравнение выражает первый закон Фика.
- градиенту концентрации. Это уравнение выражает первый закон Фика.
Изменение концентрации диффундирующего вещества по мере приближения к межфазной границе происходит нелинейно, однако если принять, что концентрация изменяется по линейному закону, то мы сможем ввести понятие эффективной толщины диффузионного слоя δ - такого расстояния от межфазной границы до зоны в которой концентрация вещества не отличается от концентрации в остальном объеме, при котором плотность диффузионного потока будет такой же, как в реальных условиях (рис. IV.12). При этом выражение для первого закона Фика можно переписать следующим образом:
 (IV.22)
(IV.22)
Если скорость электрохимического процесса ограничивается скоростью диффузии вещества, то плотность электрического тока i, протекающего через электрод (сила тока, отнесенная единице площади поверхности электрода) c учетом (IV.9,10,22) определяется как
 (IV.23)
(IV.23)
Из (IV.23) следует, что максимальная плотность тока, которая может быть достигнута в рассматриваемой ситуации, соответствует i s=0. Величина
 (IV.24)
(IV.24)
носит название предельного диффузионного тока. Из (IV.24) следует, что iD не зависит от потенциала.
Следует отметить, что если в отсутствии внешнего тока электрохимическая система находится в состоянии равновесия, то формулу связывающую плотность диффузионного тока можно вывести с использованием уравнения Нернста (IV.17).
 , (IV.25)
, (IV.25)
где Δ Е – концентрационная поляризация – отклонение электродного потенциала от равновесного значения при пропускании тока через электрод. Форма зависимости диффузионно контролируемого тока от потенциала показана на рис. (IV.13).
В случае если доставка (отвод) частиц – участников электрохимического процесса за счет их диффузии происходит достаточно быстро, то наиболее медленной стадией может стать перенос заряда через межфазную границу, т.е. сама электрохимическая реакция. При этом процесс подчиняется закономерностям, общим для всех химических реакций, а зависимость его скорости V от природы, концентрации реагентов и температуры определяется законном действия масс:
V = k П ain, (IV.26)
и уравнением Аррениуса:
k = Ae - DG# /RT, (IV.27)
где = k- константа скорости химической реакции, ai – активность i -го компонента реакции, A- предэкспоненциальный множитель, имеющий размерность k, DG# - энергия активации процесса.
Для реакции окисления металла Me → Me n+ + na e выражение для скорости процесса, выраженной в единицах плотности анодного тока ia можно записать следующим образом:
ia = aMe na F Kox exp(-D G # a/RT), (IV.28)
 где aMe – активность металла (в случае чистого металла aMe =1), Kox - константа скорости анодного процесса, G # a – энергия активации анодного процесса.
где aMe – активность металла (в случае чистого металла aMe =1), Kox - константа скорости анодного процесса, G # a – энергия активации анодного процесса.
Для реакции восстановления окислителя металла Ox + nk e → Red n- выражение для скорости процесса, выраженной в единицах плотности катодного тока ik можно записать следующим образом:
ik = ared nk F Kred exp(-D G# k /RT), (IV.29)
где aox – активность окислителя, Kred - константа скорости катодного процесса, G #k – энергия активации катодного процесса.
Рассмотрим электродную систему Me/Men+.
При равновесном потенциале E 0 D G =0. D G # a = D G#k = D G #. При отклонении потенциала от равновесного значения на величину D E изменение D G составит:
D G a = D G k = D G = - n FD E (IV.30)
С учетом соотношения Бренстеда – Поляни - Семенова:
δ(Δ G # a,k) = α a,k δ(Δ G), (IV.31)
где δ(Δ G # a,k) – изменение энергии активации анодного или катодного процесса при изменении гиббсовского потенциала процесса δ(Δ G), (0 < α a,k < 1) – коэффициент переноса анодной или катодной реакции (принято α a, обозначать β, а α k – α), при этом α + β = 1.
Из сказанного можно вывести, что для скорости электрохимической реакции Me → Me n+ + n e определяется выражением (уравнение Фольмера-Фрумкина):
ia = Koxa exp[ βn F(E-Eр)/RT], (IV.32)
где iа - скорость анодной реакции, выраженная в единицах плотности тока; а - активность реагента (в данном случае — металла); β - коэффициент переноса для анодной реакции, Ε - электродный потенциал металла в данных условиях; Ер - равновесный электродный потенциал реакции. Таким образом, скорость электрохимической реакции зависит от потенциала, изменяясь по экспоненциальному закону. Это — особенность любого электрохимического процесса, в том числе и процесса растворения металла. В форме, наиболее удобной для практического использования, уравнение (IV.32) целесообразно прологарифмировать:
ln i a = ln Kox + βn F(E-Eр)/RT, (IV.33)
или после перевода натуральных логарифмов в десятичные:
lg i a = k + βn F(E-Eр)/2,3RT, (IV.34)
где k = ln Kox /2,3, откуда получаем:
Е = a + b lg ia, (IV.35)
где b = dlg i a/d E =2,3RT/ βn F, a – постоянная.
Закон, лежащий в основе зависимости iа от Е, выражающейся уравнением (IV.35), называется уравнением Юлиуса Тафеля (Julius Tafel). Величину b соответственно называют тафелевым наклоном (имея ввиду наклон линейных кривых в координатах Ε — lg ia).
Понятие «наклон» означает, что при изменении плотности тока в 10 раз, что эквивалентно изменению логарифма этой величины на единицу, потенциал электрода, выраженный в мВ, изменяется на величину b.
По величине наклона b в ряде случаев удается судить о кинетике электрохимических реакций.
Например,наклон кривых в координатах Ε — lg i позволяет сделать заключение о числе электронов, участвующих в реакции. Рассмотрим случай, когда происходит растворение металла в одну стадию:
Me → Me n+ + na e
Предположим, что металл может переходить в раствор как в форме одновалентных Ме+, так и двухвалентных Ме2+ катионов. В любом случае для описания скорости реакции применимо уравнение (IV.35), где наклон b = 2,3RT/bnаF. Поскольку, как правило, β ~ 0,5, то при температуре 20°С при подстановке численных значений констант R и F получаем:
для случая na = 1 величина b = 118 мВ;
для случая na = 2 величина b = 59 мВ.
Для исследования электрохимических (и в частности коррозионных) процессов наиболее часто анализируют поляризационные кривые - зависимости скорости процесса от электродного потенциала и поляризационные диаграммы – графики, на которые нанесено несколько поляризационных кривых. Если на графике представлена зависимость тока от потенциала измеренная при значениях потенциала меньших значения потенциала свободной коррозии, то график называется катодной поляризационной кривой. В противном случае график называют анодной поляризационной кривой. Поляризационные кривые снимают либо в потенциостатическом режиме – записывают установившееся значение тока при заданном значении потенциала, после чего переходят к следующему значению потенциала, либо в потенциодинамическом режиме – изменяют потенциал с заданной скоростью (скорость развертки потенциала) одновременно регистрируя изменяющееся значение тока. Наиболее репрезентативно построение поляризационных кривых (и диаграмм) в полулогарифмических координатах Ε — lg i. Это связано с тем, что значения тока в пределах одного графика могут изменяться на несколько порядков величины, кроме того в таких координатах проще оценивать значения тафелевых наклонов.
 |
Схема поляризационной диаграммы показана на рис. IV.14. По вертикальной оси отложены значения потенциала, причем увеличение потенциала происходит сверху вниз. По горизонтальной оси отложены значения десятичного логарифма плотности тока. Увеличение плотности тока происходит слева направо. На графике показана катодная поляризационная кривая (1) для случая, когда восстановление окислителя происходит при кинетическом контроле. Анодная поляризационная кривая (2-6) имеет сложную форму. На участке (1) растворение металла протекает в активном режиме, т.е. характер влияния потенциала на скорость растворения подчиняется уравнению Тафеля (IV.35). Рост скорости растворения с повышением потенциала на участке (3) сменяется ее снижением – происходит пассивация металла, т.е. на его поверхности формируется защитный (пассивирующий) слой, препятствующий растворению. На участке (4) защитный слой полностью сформировался и практически не меняется с изменением потенциала. При этом растворение металла протекает с очень малой скоростью, которая практически не зависит от потенциала. Участок (5) отвечает образованию питтингов. При этом происходит локальное разрушение пассивирующего слоя и в местах разрушения скорость растворения металла резко возрастает. Такая ситуация возникает не всегда. В этом случае при повышении потенциала на участке (6) пассивирующий слой полностью разрушается (перепассивация) и скорость растворения резко возрастает. Этот эффект часто связан с тем, что с повышением потенциала изменяется степень окисления продуктов растворения металла. Экстраполяция участка (2) на пересечение с участком (1) дает точку соответствующую равенству скоростей растворения металла и восстановления окислителя. Эта точка определяет на графике потенциал свободной коррозии[2] (E кор) и плотность тока свободной коррозии (i кор). Точка перехода участка (2) в участок (3) определяет на графике критический потенциал пассивации (Eпас) и критический ток пассивации (i к) - максимальный ток, необходимый для перехода металла из активного состояния в пассивное. Проекция участка (4) на ось тока дает плотность тока растворения металла в пассивном состоянии. Потенциал, соответствующий началу участка (5) называется потенциалом питтиногобразования (Eп), а потенциал, отвечающий началу участка (6) - потенциалом перепассивации (Eп).
Для исследования электрохимических коррозионных процессов также используют некоторые другие типы данных.
Хроноаперограммы – зависимости тока от времени, снятые при постоянном значении потенциала, хронопотенциограммы – зависимости потенциала от времени, снятые при постоянном значении тока, циклические вольтамперограммы – отличаются от поляризационных кривых тем, их снимают только в потенциодинамическом режиме, причем кривые снимают многократно, зависимости импеданса электрода от потенциала и частоты колебаний потенциала и другие.
[1] Методы получения поляризационных кривых и их анализа подробно изложены в разделе III
[2] Под свободной коррозией понимают коррозию, протекающую без наложения на металл тока от внешнего источника.
Не нашли, что искали? Воспользуйтесь поиском: