Самоорганизация и самообучение нейронных сетей

Целью обучения сети с самоорганизацией на основе конкуренции нейронов считается такое упорядочение нейронов (подбор значений их весов), которое минимизирует значение ожидаемого искажения, оцениваемого погрешностью аппроксимации входного вектора значениями весов нейрона-победителя. При входных векторах и применении евклидовой метрики эта погрешность, называемая также погрешностью квантования, может быть выражена в виде

, (11.18)

где - вес нейрона-победителя при предъявлении вектора .

Этот подход также называется векторным квантованием (Vector Quantization – VQ) или кластеризацией. Номера нейронов-победителей при последовательном предъявлении векторов образуют так называемую кодовую таблицу. При классическом решении задачи кодирования применяется алгоритм -усреднений, носящий имя обобщенного алгоритма Ллойда.

Для нейронных сетей аналогом алгоритма Ллойда считается алгоритм WTA (Winner Takes All – «победитель получает все»). В соответствии с ним после предъявления вектора рассчитывается активность каждого нейрона. Победителем признается нейрон с самым сильным выходным сигналом, т.е. тот, для которого скалярное произведение оказывается наибольшим. Можно показать, что при использовании нормализованных векторов это равнозначно наименьшему эвклидову расстоянию между входным вектором и вектором весов нейронов. Победитель получает право уточнить свои веса в направлении вектора согласно правилу

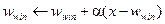, (11.19)

где - коэффициент обучения. Веса остальных нейронов уточнению не подлежат. Алгоритм позволяет учитывать «усталость» нейронов путем подсчета количества побед каждого из них и поощрять элементы с наименьшей активностью для выравнивания их шансов. Такая модификация применяется чаще всего на начальной стадии обучения с последующим отключением после активации всех нейронов. Подобный способ обучения реализован в виде режима CWTA (Conscience Winner Takes All) и считается одним из лучших и наиболее быстрых алгоритмов самоорганизации.

Помимо алгоритмов WTA, в которых в каждой итерации может обучаться только один нейрон, для обучения сетей с самоорганизацией широко применяются алгоритмы типа WTM (Winner Takes Most – «победитель получает больше»), в которых, кроме победителя, уточняют значения своих весов и нейроны из его ближайшего окружения. При этом, чем дальше какой-либо нейрон находится от победителя, тем меньше изменяются его веса. Процесс уточнения вектора весов может быть определен обобщенной зависимостью, которая здесь представляется в виде

(11.20)

для всех нейронов, расположенных в окрестности победителя. Если функция определяется в форме

, (11.21)

где 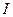обозначает номер победителя, то мы получаем классический алгоритм WTA. Очевидно, алгоритмы (11.19) и (11.20) относятся к классу рекурсивных алгоритмов стохастической аппроксимации, подробно рассмотренные в разделе 5. Существует множество вариантов алгоритма WTМ, отличающихся прежде всего формой функции . Одним из таких является классический алгоритм Кохонена.

Алгоритм Кохонена. Алгоритм Кохонена относится к наиболее давним алгоритмам обучения сетей с самоорганизацией на основе конкуренции, и в настоящее время существуют различные его версии. В классическом алгоритме Кохонена сеть инициализируется путем приписывания нейронам определенных позиций в пространстве и связывания их с соседями на постоянной основе. Такая сеть называется самоорганизующейся картой признаков (сеть SOFM – Self-Organizing Feature Map). В момент выбора победителя уточняются не только его веса, но также и веса его соседей, находящихся в ближайшей окрестности. Таким образом, нейрон-победитель подвергается адаптации вместе со своими соседями. В классическом алгоритме Кохонена функция соседства определяется в виде

. (11.22)

В этом выражении обозначает эвклидово расстояние между векторами весов нейрона-победителя 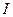и 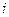-го нейрона. Коэффициент 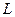выступает в роли уровня соседства, его значение уменьшается в процессе обучения до нуля. Соседство такого рода называется прямоугольным.

Другой тип соседства, часто применяемый в картах Кохонена, - это соседство гауссовского типа, при котором функция задается формулой

. (11.23)

Степень адаптации нейронов-соседей определяется не только евклидовым расстоянием между 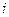-м нейроном и победителем ( 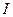-м нейроном), но также и уровнем соседства . В отличие от соседства прямоугольного типа, где каждый нейрон, находящийся в окрестности победителя, адаптировался в равной степени, при соседстве гауссовского типа уровень адаптации различен и зависит от значения функции Гаусса. Как правило «гауссовское» соседство дает лучшие результаты обучения и обеспечивает лучшую организацию сети, чем «прямоугольное» соседство.

Самоорганизующаяся карта признаков проходит два этапа обучения. На первом этапе элементы упорядочиваются так, чтобы отражать пространство входных элементов, а на втором происходит уточнение их позиций. Как правило, процесс представляется визуально путем использования двумерных данных и построения соответствующей поверхности. Например, входные векторы выбираются случайным образом на основе однородного распределения в некотором квадрате, и начинается обучение карты. В определенные моменты в ходе обучения изображения карты путем использования соответствия, показанного на рис.11.6. Элементы соединяются линиями, чтобы показать их относительное размещение. Сначала карта выглядит сильно «измятой», но постепенно в ходе обучения она разворачивается и расправляется. Конечным результатом обучения является карта, показывающая все входное пространство и являющаяся достаточно регулярной (т.е. элементы оказываются распределенными почти равномерно). Для примера была рассмотрена карта с топологией квадрата из 49 элементов, и для 250 точек данных, взятых из единичного квадрата, было проведено ее обучение, которое начиналось со случайного набора весовых значений, задающих размещение кластерных элементов в центре входного пространства, как показано на рис.11.8. На рис.11.9 и 11.10 иллюстрируется процесс разворачивания карты с течением времени. Как и для других типов сетей, в данном случае результат обучения зависит от учебных данных и выбора параметров обучения.

Рис.11.8. Весовые векторы инициализируются случайными значениями из диапазона 0,4 – 0,6

Рис.11.9. Карта по прошествии 20 итераций

Рис.11.10. Карта незадолго до окончания обучения. Элементы теперь упорядочены, и карта станет еще более регулярной по окончании финальной фазы сходимости

Контрольные вопросы к разделу №11

1. Дайте определение нейрона.

2. Каким образом организуется нейронная сеть?

3. Пояснить функцию и структуру персептрона МакКаллока-Питтса.

4. Пояснить роль вырожденного преобразования сводящегося к алгоритму (8.1).

5. Какова роль нелинейного элемента, включенного на выходе нейрона ?

6. Пояснить применимость пороговых функций (рис.8.2).

7. Каковы достоинства сигмаидального нейрона?

8. Пояснить в чем общность нейрона и алгоритмов ААР.

9. Пояснить различия нейрона и алгоритма ААР.

10. Пояснить основные виды структур НС.

11. Каковы особенности функционирования НС.

12. Пояснить решение задачи коммивояжера с помощью НС. Применимость в задачах телекоммуникации.

13. В чем суть машины Больцмана?

14. Пояснить функцию консенсуса.

15. Пояснить работу рекуррентной НС, показать общность с алгоритмами стохастической аппроксимации.

16. Пояснить работу НС при самоорганизации и самообучении.

Литература к разделу 11

1. Тарков М.С. Нейрокомпьютерные системы. – М.: Бином Лаборатория знаний, 2006 – 142 с.

2. Комашинский В.И., Смирнов Д.А. Нейронные сети и их применение в системах управления и связи. – М.: Горячая линия – Телеком, 2003.

3. Осовский С. Нейронные сети для обработки информации. – М.: ФиС, 2002.

4. Уоссерман Ф. Нейрокомпьютерная техника. М.: Мир, 1992.

Не нашли, что искали? Воспользуйтесь поиском: