Типовые задачи с решениями. № 1. Зависимость выпуска продукции от количества используемого труда отображается функцией:

№ 1. Зависимость выпуска продукции от количества используемого труда отображается функцией:

.

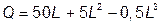1. При каком количестве используемого труда достигается максимум: а) общего выпуска; б) предельной производительности труда; в) средней производительности труда.

2. Определите эластичность выпуска по труду при использовании 5 ед. труда.

Решение

1а. Функция от одной переменной достигает максимума, когда ее производная равна нулю. С учетом того, что L > 0, получаем:

.

1б. Предельная производительность труда

достигает максимума при 10 = 3 L Þ L = 10/3.

1в. Средняя производительность труда

достигает максимума при L = 5.

2. По определению . При L = 5 средняя и предельная производительности равны 62,5; следовательно, 1.

№ 2. Фирма работает по технологии, отображаемой производствен­ной функцией Q = L ^0,75 K ^0,25. Факторы производства она покупает по неизменным ценам: w = 144; r = 3. Определите в состоянии равновесия фирмы: а) среднюю производительность труда (продукт труда); б) среднюю производительность капитала (продукт капитала); в) предельную производительность труда; г) предельную производительность капитала.

Решение

а) . Условие равновесия фирмы MRTS_L,K = w/r.

.

Следовательно: .

б) → .

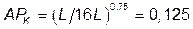в) .

г) .

№ 3. Технология производства фирмы задана производственной функцией:

Q = 20 L ^0,5. Цена труда w = 2, а цена продукции фирмы Р = 5. Определите: а) выпуск фирмы; б) общие затраты на выпуск; в) средние затраты; г) предельные затраты; д) объем спроса фирмы на труд.

Решение

а) В соответствии с технологией . Поэтому 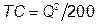и .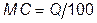

По условию максимизации прибыли

.

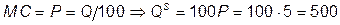б) TC = 500²/200 = 1250; в) AC = 1250/500 = 2,5;

г) MC = 500/100 = 5; д) L = 500²/400 = 625.

№ 4. Фирма, максимизирующая прибыль, работает по технологии Q = L ^0,25 K ^0,25. Факторы производства она покупает по неизменным ценам: w = 2; r = 8 и продает свою продукцию по цене Р = 320. Определите: а) выпуск фирмы; б) общие затраты на выпуск; в) средние затраты; г) предельные затраты; д) объем спроса фирмы на труд; е) объем спроса фирмы на капитал; ж) прибыль фирмы; з) излишки продавца.

Решение:

.

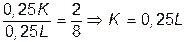В соответствии с технологией: . Следовательно:

.

Тогда . Из условия максимизации прибыли следует .

б) LTC = 8×20² = 3200; в) LAC = 3200/20 = 160;

г) LMC = 16×20 = 320; д) L = 2×400 = 800;

е) K = 0,5×400 = 200; ж) 20×320 – 3200 = 3200.

з) 0,5•20•320 = 3200

№ 5. Фирма с функцией общих затрат

может продать любое количество своей продукции по цене Р = 20.

1. Определите выпуск фирмы, а) минимизирующий средние затраты; б) максимизирующий прибыль.

2. Рассчитайте максимальную величину: а) прибыли;

б) излишка производителя.

3. Определите эластичность предложения фирмы по цене, когда она получает максимум прибыли.

Решение

1а. .

1б. .

2а. p = 20×3 – 8 – 8×3 – 2×9 = 10.

2б. D = 20×3 – 8×3 – 2×9 = 18.

3. .

№ 6. При цене 8 ден. ед. за 1 кг фермер, имеющий линейную функцию предложения, продал 10 кг яблок. Эластичность предложения по цене равна 1,6. Сколько кг яблок продаст фермер, если цена будет равна 12 ден. ед?

Решение

Общий вид линейной функции предложения: Q^S = m + nP.

Для нее e^S = nP*/Q* Þ n = e^SQ*/P*; m = Q* (1 – e^S).

В условиях задачи n = 2; m = 6; следовательно, функция предложения имеет вид

Q^S = – 6 + 2 P; при цене 12 объем предложения равен 18.

№ 7. На рынке имеются три продавца со следующими функциями предложения:

Определите эластичность рыночного предложения по цене, когда на рынке продается 11 ед. товара.

Решение

Для определения интервалов цен, соответствующих различным наклонам кривой рыночного предложения, перейдем от индивидуальных функций предложения к индивидуальным функциям цены предложения:

Следовательно, в интервале 0 < P £ 4 рыночное предложение представлено продавцом I; в интервале 4 < P £ 8 рыночное предложение равно сумме предложения I и III продавцов и только после P > 8 рыночное предложение равно сумме всех трех продавцов:

Отсюда видно, что 11 ед. товара будет продано по цене Р = 5; тогда e^S = 3×5/11 = 15/11.

Рис. 1. Рыночное предложение как сумма индивидуальных предложений

Задачи

№ 1. Зависимость выпуска продукции от количества используемого труда отображается функцией

.

1. При каком количестве используемого труда достигается максимум: а) общего выпуска; б) предельной производительности труда; в) средней производительности труда.

2. Определите эластичность выпуска по труду при использовании 5 ед. труда.

№ 2. Зависимость выпуска продукции от количества используемого труда отображается функцией: . Определите максимум: а) общего выпуска; б) предельной производительности труда; в) средней производительности труда.

№ 3. Фирма работает по технологии, отображаемой производствен­ной функцией Q = 10 L ^0,75 K ^0,25. Факторы производства она покупает по неизменным ценам: w = 24; r = 8. Определите в состоянии равновесия фирмы: а) среднюю производительность труда (продукт труда); б) среднюю производительность капитала (продукт капитала); в) предельную производительность труда; г) предельную производительность капитала.

№ 4. Фирма работает по технологии, отображаемой производствен­ной функцией Q = 10 L ^0,75 K ^0,25. Факторы производства она покупает по неизменным ценам: w = 5; r = 1. Определите в состоянии равновесия фирмы: а) среднюю производительность труда (продукт труда); б) среднюю производительность капитала (продукт капитала); в) предельную производительность труда; г) предельную производительность капитала.

№ 5. Технология производства фирмы задана производственной функцией:

Q = 10 L ^0,75. Цена труда w = 5, а цена продукции фирмы Р = 2. Определите: а) выпуск фирмы; б) общие затраты на выпуск; в) средние затраты; г) предельные затраты; д) объем спроса фирмы на труд.

№ 6. Технология производства фирмы задана производственной функцией:

Q = 10 L ^0,75. Цена труда w = 5, а цена продукции фирмы Р = 4. Определите: а) выпуск фирмы; б) общие затраты на выпуск; в) средние затраты; г) предельные затраты; д) объем спроса фирмы на труд.

№ 7. Фирма, максимизирующая прибыль, работает по технологии Q = L ^0,5 K ^0,25. Факторы производства она покупает по неизменным ценам: w = 10; r = 5 и продает свою продукцию по цене Р = 100. Определите: а) выпуск фирмы; б) общие затраты на выпуск; в) средние затраты; г) предельные затраты; д) объем спроса фирмы на труд; е) объем спроса фирмы на капитал; ж) прибыль фирмы; з) излишки производителя.

№ 8. Фирма, максимизирующая прибыль, работает по технологии Q = L ^0,5 K ^0,25. Факторы производства она покупает по неизменным ценам: w = 1; r = 4 и продает свою продукцию по цене Р = 20. Определите: а) выпуск фирмы; б) общие затраты на выпуск; в) средние затраты; г) предельные затраты; д) объем спроса фирмы на труд; е) объем спроса фирмы на капитал; ж) прибыль фирмы; з) излишки производителя.

№ 9. Фирма с функцией общих затрат может продать любое количество своей продукции по цене Р = 24.

1. Определите выпуск фирмы, а) минимизирующий средние затраты; б) максимизирующий прибыль.

2. Рассчитайте максимальную величину: а) прибыли; б) излишка производителя.

3. Определите эластичность предложения фирмы по цене, когда она получает максимум прибыли.

№ 10. Фирма с функцией общих затрат может продать любое количество своей продукции по цене Р = 20.

1. Определите выпуск фирмы, а) минимизирующий средние затраты; б) максимизирующий прибыль.

2. Рассчитайте максимальную величину: а) прибыли; б) излишка производителя.

3. Определите эластичность предложения фирмы по цене, когда она получает максимум прибыли.

№ 11. Фирма с функцией общих затрат может продать любое количество своей продукции по цене Р = 20.

1. Насколько объем выпуска, максимизирующий прибыль, больше объема выпуска, минимизирующего средние затраты?

2. Во сколько раз максимальные излишки производителя превышают максимальную прибыль?

№ 12. Общие затраты конкурентной фирмы равны . Рассчитайте, насколько при повышении цены на продукцию фирмы с 10 до 12: а) возрастет излишек производителя; б) уменьшится эластичность предложения по цене.

№ 13. При цене 8 ден. ед. за 1 кг фермер, имеющий линейную функцию предложения, продал 10 кг яблок. Эластичность предложения по цене равна 2.

1. Сколько кг яблок продаст фермер, если цена будет равна 12 ден. ед.?

2. При какой цене фермер предложит 30 кг яблок?

№ 14. При цене 10 ден. ед. за 1 кг фермер, имеющий линейную функцию предложения, продал 15 кг яблок. Эластичность предложения по цене равна 2.

1. Сколько кг яблок продаст фермер, если цена будет равна 16 ден. ед?

2. При какой цене фермер предложит 45 кг яблок?

№ 15. Фирма, максимизирующая прибыль, работает по технологии Q = L ^0,5 K ^0,25. Факторы производства она покупает по неизменным ценам. Определите эластичность предложения фирмы по цене.

№ 16. Фирма, максимизирующая прибыль, работает по технологии Q = L ^0,25 K ^0,25. Факторы производства она покупает по неизменным ценам. Определите эластичность предложения фирмы по цене.

№ 17. Фермер желает организовать производство в регионе, в котором имеется 80 га земли и можно нанять 120 ед. труда. Технология производства сельскохозяйственной продукции отображается функцией Q = L ^0,3 K ^0,6. Приняв ставку заработной платы за 1, установите такую ставку арендной платы за землю, чтобы фермер производил максимально возможный объем продукции.

№ 18. Фермер желает организовать производство в регионе, в котором имеется 80 га земли и можно нанять 200 ед. труда. Технология производства сельскохозяйственной продукции отображается функцией Q = L ^0,3 K ^0,6. Приняв ставку заработной платы за 1, установите такую ставку арендной платы за землю, чтобы фермер производил максимально возможный объем продукции.

№ 19. Функция общих затрат конкурентной фирмы – TC = 48 + 10 Q – Q ² + 0,5 Q ³. Во вторник фирма продала 10 ед. продукции, а в среду 12 ед. Насколько в указанный период возросла: а) цена продукции? б) прибыль фирмы?

№ 20. Функция общих затрат конкурентной фирмы – TC = 100 + 10 Q – 2 Q ² + 0,5 Q ³. Во вторник фирма продала 13 ед. продукции, а в среду 15 ед. Насколько в указанный период возросла: а) цена продукции? б) прибыль фирмы?

№ 21. Рассчитать постоянные, переменные, предельные, средние общие, средние постоянные и средние переменные затраты. Последние четыре величины изобразить графически. Зависимость общих затрат предприятия представлена в таблице:

№ 22. На рынке имеются три продавца со следующими функциями предложения:

1. Сколько единиц товара будет продано на рынке при Р = 10?

2. При какой цене можно будет продать 35 единиц товара?

3. Какова эластичность предложения по цене при Р = 11?

4. Какова эластичность предложения по цене при Q = 32?

№ 23. В течение года предприятие, оцениваемое в 2 млрд. ден. ед., затратило 300 млн ден. ед. на сырье и материалы, 100 млн ден. ед. на топливо и энергию и 400 млн ден. ед. на зарплату персонала. Выручка от реализации продукции за тот же период составила 1 млрд ден. ед. Владелец предприятия, являющийся одновременно его управляющим, мог бы в случае закрытия дела найти работу с месячной зарплатой в 1 млн ден. ед. Годовая ставка процента составляет 10%. Рассчитать бухгалтерскую и экономическую прибыль.

№ 24. Владелец небольшой фирмы работает сам и нанимает двух помощников, выплачивая им по 400 тыс. ден. ед. в месяц и 200 тыс. ден. ед. себе. Затраты на сырье составляют 3 млн ден. ед., аренда помещения обходится в 1 млн ден. ед. в месяц. Собственный капитал мог бы приносить владельцу при ином варианте его использования 500 тыс. ден. ед. в месяц, а работа по специальности в крупной корпорации – 600 тыс. ден. ед. Месячная выручка фирмы составляет 6 млн ден. ед. Стоит ли предпринимателю продолжать дело?

Не нашли, что искали? Воспользуйтесь поиском: