Геометрическая интерпретация потока

Поле всякого вектора 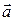можно задать с помощью линий, аналогичных силовым линиям . Представление поля с помощью линий вектора является весьма неточным, но очень полезно для наглядного представления о поле. В рамках этого представления потоку вектора можно придать очень наглядную геометрическую интерпретацию. При этом будем предполагать, что количество линий вектора достаточно для представления модуля вектора с заданной точностью.

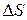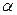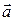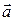Для плоского элемента поверхности , нормаль к которому образует угол c вектором , число пересечений линий вектора с 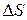равно произведению густоты линий (т.е. модуля вектора) на площадь площадки, расположенной перпендикулярно силовым линиям в данной точке пространства. Очевидно, что количество линий, пересекающих и 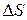одинаково, а площади связаны соотношением:

. (13.09)

Поэтому

(13.10)

Поток вектора выражается таким же соотношением. Поэтому можно утверждать, что поток вектора через некоторую поверхность численно равен количеству пересечений линий вектора с этой поверхностью:

(13.11)

Необходимо, однако, учесть, что поток – величина алгебраическая. Если на рисунке 13.2 направление линий вектора изменить на противоположное, то поток станет отрицательным. Для совпадения знаков и пересечения с острым углом 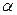считают положительными, а с тупым 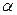– отрицательными.

Большое значение имеет рассмотрение потока вектора через замкнутую поверхность. Для замкнутых поверхностей положительной считается внешняя нормаль 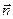и с «+» берутся пересечения, связанные с выходом наружу линий вектора. Пересечения при входе внутрь берутся с « – ».

Обратим внимание на то, что если линии вектора непрерывны внутри поверхности, то каждая линия пересекает поверхность четное число раз: половину с «+», половину с « – » и, соответственно поток через поверхность оказывается равным нулю.