Энергия заряженного конденсатора

Заряд 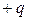положительно заряженной обкладки конденсатора находится в практически однородном поле отрицательно заряженной пластины в точках с потенциалом 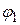. Аналогичным образом отрицательный заряд 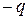находится в точках с потенциалом 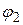. Поэтому энергия конденсатора

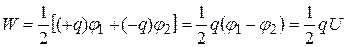Очевидно, что эту формулу можно представить в виде

или

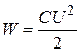Формула (16.17) связывает энергию конденсатора с наличием на его обкладках заряда, а (16.18) – с существованием в промежутке между обкладками электрического поля. В связи с этим возникает вопрос о локализации энергии электрического поля: на зарядах или в пространстве между обкладками. В рамках электростатики ответить на этот вопрос невозможно, однако электродинамика утверждает, что электрическое и магнитное поля могут существовать независимо от зарядов. Поэтому энергия конденсатора сосредоточена в пространстве между обкладками конденсатора и связана с электрическим полем конденсатора.

Поскольку поле плоского конденсатора является однородным, можно считать, что энергия распределена между обкладками конденсатора с некоторой постоянной плотностью 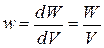. В соответствии с соотношением (16.18)

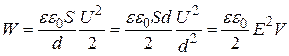Поэтому плотность энергии электрического поля конденсатора оказывается равной

Учтем, что 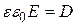, т.е. электрической индукции. Тогда выражению для плотности энергии можно придать вид:

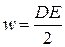Электрическая индукция в соответствии с определением:

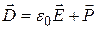где - поляризованность диэлектрика между обкладками конденсатора. Тогда выражение для плотности энергии приобретает вид:

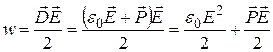Первое слагаемое в правой части (16.23) представляет собой энергию, которой обладал бы конденсатор, если в пространстве между обкладками был бы вакуум. Второе слагаемое связано с энергией, затрачиваемой при зарядке конденсатора на поляризацию диэлектрика, заключенного в пространстве между обкладками.

Не нашли, что искали? Воспользуйтесь поиском: