Затухающие колебания.

Во всяком реальном контуре обязательно присутствует активное сопротивление R. Соответственно выражение для закона Ома будет иметь вид (21.03):

или . (21.14)

Разделим (21.14) на и воспользуемся обозначением:

. (21.15)

Получаем дифференциальное уравнение, описывающее колебания в контуре с ненулевым активным сопротивлением:

(21.16)

Параметр называется коэффициентом затухания. По смыслу эта величина обратна времени, в течение которого амплитуда колебаний уменьшается в «е» раз.

Решение (21.16) при не слишком большом затухании имеет вид (как известно!):

(21.17)

«…при не слишком большом затухании» означает:

. (21.18)

В этом случае циклическая частота колебаний остается вещественной:

. (21.19)

Из (21.19) следует, что частота затухающих (т.е. при ненулевом сопротивлении в контуре) колебаний меньше собственной.

Для характеристики степени затухания колебаний используют логарифмический декремент затухания, который определяется соотношением:

. (21.20)

Напомним, что есть количество колебаний, совершаемых системой за время, пока амплитуда колебаний уменьшается в «е» раз.

В нашем случае и , поэтому

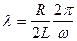. (21.21)

поскольку определяется параметрами контура , то логарифмический декремент затухания l является характеристикой контура. Важно отметить, что соотношение (21.21) справедливо всегда, в отличии от широко используемого приближенного соотношения, которое мы сейчас рассмотрим.

При небольшом затухании ,и вторым слагаемым в (21.19) можно пренебречь. Тогда

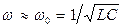. (21.22)

. (21.23)

Чаще для характеристики степени затухания колебаний используется добротность контура:

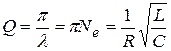. (21.24)

Добротность контура, как и любой колебательной системы, пропорциональна .

Энергия, запасённая в контуре, пропорциональна квадрату напряжения на конденсаторе, а значит, уменьшается по закону:

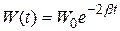. (21.25)

Тогда отношение энергии DW, теряемой в контуре за период к запасённой 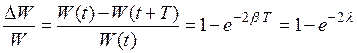. (21.26)

Если (!) затухание невелико: l << 1, то , а значит

. (21.27)Отсюда находим, что

. (21.27)

Другими словами добротность пропорциональна отношению энергии запасённой в контуре к энергии, теряемой за период.

Не нашли, что искали? Воспользуйтесь поиском: