Вынужденные электрические колебания. Вынeужденные колебания можно осуществить, например, включив последовательно с элементами контура переменную ЭДС:

Вынeужденные колебания можно осуществить, например, включив последовательно с элементами контура переменную ЭДС:

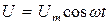(21.28)

В выражении для закона Ома это напряжение следует сложить с действующими в контуре напряжениями:

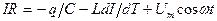(21.30)

или

(21.31)

Установившиеся колебания описываются в этом случае решением уравнения (21.31), которое имеет вид:

, (21.32)

т.е. колебания происходят на частоте вынуждающей силы. Кроме того, амплитуда колебаний заряда на конденсаторе зависит от частоты:

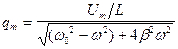, (21.33)

а между колебаниями внешнего напряжения и колебаниями заряда на конденсаторе существует сдвиг фаз: колебания заряда отстают по фазе от внешнего напряжения на угол 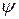, который определяется соотношением:

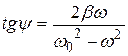. (21.34)

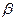В случае электромагнитных колебаний, подставив в (21.33) и (21.34) значения параметров и , получим соотношения:

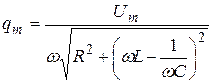. (21.35)

и

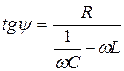. (21.36)

Сила тока в контуре при установившихся колебаниях определяется соотношением:

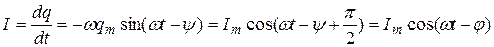. (21.37)

где (21.38)

– сдвиг фаз между током и приложенным внешним напряжением.

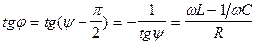. (21.39)

Таким образом, знак сдвига фаз между приложенным напряжением и током в цепи определяется знаком разности .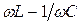

Амплитуда колебаний силы тока, в соответствии с (21.37) получается умножением амплитуды колебаний заряда на 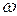и определяется соотношением:

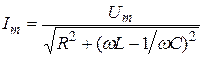. (21.40)

Исходное уравнение колебаний (21.30) в каждый момент времени можно представить в виде:

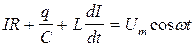. (21.41)

Слагаемые в левой части (21.41) есть напряжения на соответствующих участках цепи:

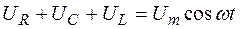(21.42)

Поэтому можно сказать, что в данный момент времени сумма напряжений на элементах контура равна напряжению, приложенному извне.

Падение напряжения наактивном сопротивлении R

. (21.43)

Можно утверждать, что фазы напряжения и тока на активном сопротивлении совпадают.

Напряжение на ёмкости 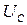получим, разделив выражение для заряда на его емкость :

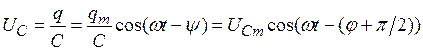(21.44)

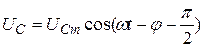. (21.45)

Сравнивая это соотношение с (21.43), видим, что напряжение на ёмкости отстаёт по фазе от силы тока на .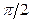

Максимальное значение (амплитудное)

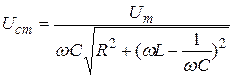. (21.45)

.Однако в соответствии с (21.40) 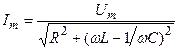. Поэтому можно утверждать, что амплитудное значение напряжение на конденсаторе и амплитуда тока в контуре связаны простым соотношением:

. (21.46)

Не нашли, что искали? Воспользуйтесь поиском: