Многолучевая интерференция

Допустим, что в некоторую точку экрана приходит N когерентных лучей с одинаковой интенсивностью. При этом фаза каждого последующего луча сдвинута относительно предыдущего на постоянную величину 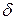. Рассмотрим интерференционную картину, возникающую в этом случае.

Колебания,возбуждаемые лучами можно представить в виде экспонент:

………………………….. (1)

…………………………..

Результирующее колебание в точке наблюдения равно сумме колебаний (1):

(2)

Сумма в соотношении (2) представляет собой сумму N членов геометрической прогрессии с единичным первым членом, знаменателем и последним членом .

Известно, что сумма членов геометрической прогрессии определяется формулой:

(q – знаменатель прогрессии, b ₁ и b_n – первый и последний члены).

Поэтому результирующее колебание в (2) представим в виде:

, (3)

где – комплексная амплитуда результирующего колебания.

По определению комплексной амплитуды

,

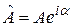где - обычная амплитуда, а - начальная фаза.

Для нахождения квадрата амплитуды результирующего колебания (которому пропорциональна интенсивность света в данной точке) найдем произведение (комплексной амплитуды и комплексно сопряженной):

В соответствии с формулой Эйлера . Поэтому , а . Тогда

(4)

Каждый из лучей создает в точке наблюдения интенсивность, пропорциональную квадрату его амплитуды – (k – коэффициент пропорциональности). Тогда результирующая интенсивность

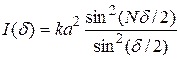. (5)

Из (5) видно, что при значениях

(6)

дробь в соотношении (5) становится неопределенной. Значение дроби получим, взяв предел при . Воспользовавшись дважды правилом Лопиталя, получим:

. (7)

Следовательно, в точках экрана, где выполняется условие (6), для интенсивности света справедливо соотношение:

, (8)

а значит интенсивность в N² раз больше по сравнению с интенсивностью от одного луча. Эти точки называются главными максимумами интерференционной картины, условие (6) – условием наблюдения главного максимума, число m называется порядком главного максимума.

Рассмотрим подробнее изменение интенсивности в промежутке между двумя главными максимумами.

В соотношении (5) при изменении m на единицу, т.е. при переходе к соседнему главному максимуму, d меняется на 2 p, а d/2 – на p. (). Следовательно, в промежутке между двумя главными максимумами знаменатель везде, кроме концов, конечен.

Представим, что плавно изменяется на p. Тогда аргумент синуса в числителе – N d /2 – изменяется на N p. При этом он проходит значения

N d/2 = p, 2 p,…(N - 1) p,

в которых числитель обращается в нуль. Всего таких значений имеется N – 1. Следовательно, в промежутке между соседними главными максимумами на экране располагается N - 1 минимум. Этим минимумам отвечает условие:

d = 2p, =1, 2, 3, … N – 1.

Поскольку при плавном изменении d числитель изменяется периодически по закону синуса, а знаменатель при этом конечен, то в промежутках между минимумами естественно располагаются максимумы, которые называют вторичными. У вторичных максимумов, ближайших к главному интенсивность максимальна, вследствие того, что синус в знаменателе при приближении к краям рассматриваемого интервала изменения d уменьшается. Но, можно показать, что она не превышает 1/22 интенсивности главного максимума. Итоговая интерференционная картина имеет вид, показанный на рисунке.

Пунктиром на рисунке показано распределение интенсивности по экрану в случае двух источников – N = 2 (например, для двух щелей в опыте Юнга). Очевидно, что с ростом N главное максимумы сужаются. Действительно, первое нулевое значение синуса в числителе – 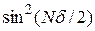– c ростом N наблюдается при меньшем . При этом интенсивность света в точках главных максимумов возрастает ().

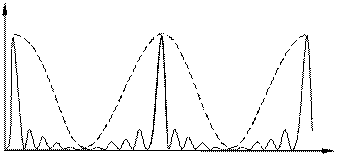
Рисунок 1.

Не нашли, что искали? Воспользуйтесь поиском: