ЭКСПЕРИМЕНТАЛЬНЫЕ ИЗОТЕРМЫ

Лекция 16. МОДЕЛЬ ИДЕАЛЬНОГО ГАЗА. ОСНОВНОЕ УРАВНЕНИЕ

МОЛЕКУЛЯРНО - КИНЕТИЧЕСКОЙ ТЕОРИИ ГАЗОВ. УРАВНЕНИЕ

КЛАПЕЙРОНА — МЕНДЕЛЕЕВА. УРАВНЕНИЕ СОСТОЯНИЯ

РЕАЛЬНОГО ГАЗА. ИЗОТЕРМЫ ВАН-ДЕР-ВААЛЬСА.

ЭКСПЕРИМЕНТАЛЬНЫЕ ИЗОТЕРМЫ

1. Модель идеального газа. Основное уравнение

молекулярно-кинетической теории газов.

Уравнение Клапейрона—Менделеева

Молекулярно-кинетическая теория, исходя из анализа движения и взаимодействия отдельных молекул, объясняет свойства газообразного состояния вещества и происходящие в газах явления, устанавливает связь между непосредственно определенными на опыте макроскопическими параметрами (давление, температура и т. д.) газа и величинами, характеризуемыми свойствами отдельных молекул.

Эта связь имеет наиболее простой вид для идеального газа, молекулы которого принимаются за материальные точ­ки, не взаимодействующие друг с другом на расстоянии (следовательно, потенциальная энергия молекул такого газа равна нулю). Все возможные взаимодействия молекул идеальногo газа сводятся к их столкновениям. При этом считается, что столкновения молекул друг с другом и с другими телами происходят абсолютно упруго.

Остановимся на выводе основного уравнения молекулярно-кинетической теории газа.

Для этого определим давление газа, оказываемое им на стенки сосуда, в котором он находится. Давление определяется силами, возникающими при столкновении молекул со стенками.

Пусть некоторая молекула газа массой m_а, имеющая скорость упруго соударяется со стенкой АВ сосуда (рис. 17.1).

Разложим скорость на три составляющие по осям х, у и z:

, и ; причем ось х направим перпендикулярно стенке, оси у и z параллельно стенке. Как видно из рисунка, в peзультате упругого удара перпендикулярная стенке составляющая скорости изменила направление на противоположное, две другие составляющие и не изменились ( nepпендикулярна плоскости рисунка и поэтому не обозначена). До удара (в перпендикулярном направлении к стенке) молекула имела импульс величиной m_aυ_x, после удара - m_aυ_x. Таким образом, изменение импульса молекулы равно

m_aυ_x— (—m_aυ_x) = 2 m_aυ_x.

Согласно закону сохраненш импульса, такой же импульс, но противоположно направленный получит стенка. Это изменение импульса стенки равно импульсу силы f, действующей со стороны молекулы на стенку за время удара τ:

fτ = 2 m_aυ_x. (16.1)

Пусть о площадку S, перпендикулярную оси х, за время τ ударяется N молекул, имеющих одинаковые составляющие υ_x вдоль оси х. В результате соударения молекул с площадкой S общее изменение импульса стенки согласно (16.1) равно

Fτ=2 m_aυ_xN, (16.2)

где F=Nf — сила, действующая на стенку со стороны всех молекул. Число молекул N найдем из следующих соображений. За время τ до площадки S дойдут лишь те молекулы, которые лежат от нее не далее, чем на расстоянии υ_xτ (рис. 17.2), т. е. те молекулы, которые заключены в объеме цилиндра площадью S и образующей υ_xτ. Если в единице объема содержится п' молекул, имеющих одинаковые состав­ляющие υ_x, то в объеме цилиндра их будет υ_xτSn′. Молекулы движутся хаотично, поэтому все направления движения рав­ноправны. Следовательно, вдоль оси х половина молекул, за­ключенных в цилиндре, движется к стенке S, другая половина — от нее. Вследствие этого за время τ о площадку S ударяется

(16.3)

молекул. Из формул (16.2) и (16.3) получаем среднюю силу F, действующую со стороны всех молекул на площадку S:

F =n'm_a υ_x²S.

Откуда величина давления

(16.4)

Пусть теперь имеем в единице объема п молекул с раз­личными скоростями: п₁ молекул имеют скорость υ₁, n ₂ - скорость υ ₂ и т. д., так что

.

Обозначим перпендикулярные площадке S составляющие скоростей молекул через υ_x1, υ_x2, …,υ_xn. Давление на площадку S будет равно сумме давлений, оказываемых со стороны всех групп молекул. Согласно формуле (16.4) имеем:

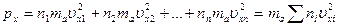. (16.5)

Точно такие же формулы мы получим для площадок S, перпендикулярных осям у и z:

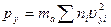и .(16.6)

Ввиду полной хаотичности движений молекул давление газа в любом направлении должно быть одинаковым, поэтому

р_х = р_у = р_г = р.

Сложив уравнения (16.5) и (16.6), получим

. (16.7)

Поскольку сумма квадратов составляющих скорости равна квадрату скорости

,

то формулу (16.7) можно записать в виде

. (16.8)

Величина

(16.9)

является средней квадратичной скоростью молекул газа. Используя (16.9), выражение (16.8) запишем в виде

или иначе:

,

где - средняя кинетическая энергия молекулы.

Формула

(16.10)

называется основным уравнением молекулярно-кинетической теории. Это уравнение устанавливает связь между средним значением микроскопической величины, характеризующей состояние молекулы — кинетической энергией поступатель­но движения молекулы, и термодинамическим параметром, определяющим макроскопическое состояние системы — давлением р.

Экспериментально измерить непосредственно чрезвычайно трудно, поэтому формулу (16.10) целесообразно преобразовать так, чтобы в нее входили только термодинамичесие параметры.

Использовав формулы (15.7) и (16.10), приходим к урав­нению

p = nkT. (16.11)

Выразим концентрацию п газа, находящегося в объеме V,черезмассу газа m, молярную массу М и число Авогадро N_A:

.

Подставим это выражение п в (16.11):

. (16.12)

Произведение kN_A есть универсальная газовая постоянная R = kN_A. Таким образом, (16.12) можно записать

. (16.13)

Выражение (17.13) представляет собой уравнение Клапейрона—Менделеева, или иначе уравнение состояния идеального газа. Это уравнение оказывается справедливым и для реальных газов в довольно большом диапазоне давлений. Поэтому оно часто используется в инженерной практике.

Не нашли, что искали? Воспользуйтесь поиском: