Уравнение состояния реального газа

При выводе уравнения Клапейрона—Менделеева (16.13) мы пренебрегали размерами молекул и их взаимодействием друг с другом. Вместе с тем, при повышении давления возрастает плотность газа, что приводит к изменению среднего расстояния между молекулами, в результате чего собственый объем молекул и их взаимодействие друг с другом начинают играть существенную роль. Поэтому для реальных газов с повышением давления и уменьшением температуры наблюдаются все большие и большие отклонения от уравнения Клапейрона—Менделеева.

Из большого числа уравнений, предложенных для описа­ния поведения реального газа, самым простым и в то же время дающим хорошие результаты оказалось уравнение Ван-дер-Ваальса. Оно было получено путем внесения попра­вок b и p_i на объем, занимаемый молекулами и их взаимо­действие, в уравнение Клапейрона (уравнение (16.13), напи­санное для одного моля):

(p+p_i)(V₀ ─ b) = RT. (17.14)

Оценим величины поправок b и p_i. Часть объема, недоступная для движения молекул вследствие их размеров, определяет поправка b. Ее можно связать с эффективным радиу­сом молекул r. Пусть в сосуде имеются лишь две молекулы (рис. 17.3). Центры молекул O₁ и О₂ могут приблизиться друг к другу на расстояние, равное эффективному диа­метру молекулы d. Следовательно, для обеих молекул оказы­вается недоступным сферический объем радиуса d:

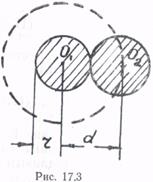
или, так как d = 2r,

,

где 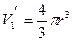— объем одной молекулы.

Соответственно для одной молекулы оказывается недо­ступным объем

.

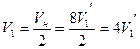Если в сосуде находится 1 моль газа, то для всех N_A его молекул недоступным оказывается объем

.

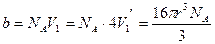Отметим, что при выводе поправки b пренебрегли тем, что молекулы не могут подойти к стенке ближе, чем па эффек­тивный радиус молекулы r. Следовательно, для молекул не­доступен слой толщиною r, прилегающий к стенке. Если пло­щадь поверхности сосуда S, то объем недоступного слоя равен S∙r. Очевидно, такое пренебрежение при выводе можно делать, если объем S∙r много меньше объема сосуда с газом.

Теперь оценим вторую поправку p_i, входящую в уравне­ние Ван-дер-Ваальса (16.14), обусловленную взаимодейст­вием молекул. При больших расстояниях между молекулами молекулярные силы являются силами притяжения и называ­ются силами Ван-дер-Ваальса. Своим происхождением силы Ван-дер-Ваальса обязаны наличием вокруг молекул собст­венного электромагнитного поля, собственного или наведен­ного внешним полем электрического момента. На близких расстояниях, когда электронные оболочки взаимодействую­щих молекул взаимно проникают друг в друга, возникают силы отталкивания, превосходящие силы притяжения.

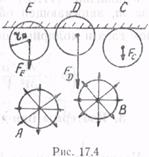Для определения поправки р_i нужно рассмотреть влияние на взаимодействие молекул, находящихся вблизи стенок со­суда, сил Ван-дер-Ваальса. Пусть действие Ван-дер-Ваальсовых сил распространяется на расстояние r_в. Окружим каж­дую молекулу сферой молекулярного действия (т. е. прове­дем около нее сферу радиусом r_в). Если эта сфера находится внутри газа, то результирующая сила, действующая на дан­ную молекулу, равна нулю, поскольку действие ближайших соседей взаимно компенсируется (рис. 17.4, молекулы А и В). Иначе обстоит дело для моле­кул, находящихся вблизи стенок сосуда — для них сфера молеку­лярного действия лишь частично проходит в газе (рис. 17.4, моле­кулы E, D, С). Поэтому для мо­лекул, находящихся вблизи стен­ки, возникают силы F_E, F_D, F_C, направленные внутрь газа, при­чем тем больше, чем ближе рас­положена молекула к стенке. Та­ким образом, в отличие от идеального газа импульс молекул,

налетающих на стенку, изменяется не только под действием сил давления со стороны стенки, но и под действием Ван-дер-Ваальсовых сил (рис. 17.4, F_E, F_D, F_C), «тянущих» молекулы внутрь газа. В результате газ находится под большим давлением р', чем то давление, которое на него оказывают стен­ки сосуда: р' = р + р_i. Величина р_i называется внутренним давлением газа.

Очевидно, сила, «оттягивающая» молекулу из слоя вблизи стенки, пропорциональна концентрации молекул газа. С дру­гой стороны, число молекул, находящихся в слое вблизи стенки, также пропорционально концентрации п. Следовательно, сила, действующая на все молекулы прилегающего к стенке слоя и направленная внутрь сосуда, должна быть пропорциональна n ². Эта сила, отнесенная к единице площа­ди, и определяет внутреннее давление р_i:

р_i ~ n ².

Итак,

,

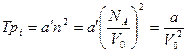где V₀ — объем одного моля; а' и 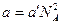— коэффициенты, зависящие от рода газа. Таким образом, с учетом обеих по­правок p_i и b уравнение (16.14) можно записать:

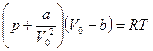. (16.15)

Это уравнение Ван-дер-Ваальса для одного моля, спра­ведливое для условий b<<V₀ и << p, и, как показывает опыт, для не очень высоких давлений.

Уравнение (16.15) можно записать и для любой массы газа m, занимающей объем V, используя связь между объемом газа и молярным объемом V₀ ():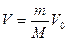

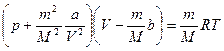. (16.16)

Не нашли, что искали? Воспользуйтесь поиском: