
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Гранулометричного складу
Таблиця 2.2
| Різновид грунтів | Вміст частинок за розміром в % від маси сухого грунту | |||
| Великоуламкові: | ||||
| Валунний грунт (глибистий) | Маса частинок більших 200 мм перевищує 50 % | |||
| Гальковий грунт (щебенистий) | Маса частинок більших 10 мм перевищує 50 % | |||
| Гравійний грунт (жорств’яний) | Маса частинок більших 2 мм перевищує 50 % | |||
| Піщані: | ||||
| Піски гравіюваті | Маса частинок більших 2 мм перевищує 25 % | |||
| Піски крупні | Маса частинок більших 0,5 мм перевищує 50 % | |||
| Піски середньої крупності | Маса частинок більших 0,25 мм перевищує 50 % | |||
| Піски дрібні | Маса частинок більших 0,1 мм 75 % і більше | |||
| Піски пилуваті | Маса частинок більших 0,1 мм менше 75 % | |||
Для класифікації глинистих грунтів використовують показник, який називається числом пластичності 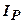
 , де (2.18)
, де (2.18)
 - вологість на межі текучості (вологість, при якій грунт переходить з пластичного стану в текучий);
- вологість на межі текучості (вологість, при якій грунт переходить з пластичного стану в текучий); 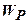 - вологість на межі розкочування (вологість, при якій грунт переходить з твердого стану в пластичний).
- вологість на межі розкочування (вологість, при якій грунт переходить з твердого стану в пластичний).
Вологість на межі текучості відповідає такій вологості грунту, при якій ста-ндартний балансирний конус масою 76 г занурюється в грунтове тісто на 10 мм за 5 с.
Методика випробувань викладена в [3].
Вологість грунту відповідає вологості на межі розкочування, коли джгутики грунтового тіста діаметром 3 мм розпадаються в процесі розкочування на елементи довжиною 3...10 мм. При більшому діаметрі грунт знаходиться в твердому стані (недостатня вологість), а при меншому - в пластичному стані (надмірна вологість).
Методика випробувань викладена в [3].
Великий вміст у грунтах глинистих частинок збільшує питому поверхню грунту, відповідно, збільшується кількість води, необхідної для переходу грунту з твердого стану в текучий. І навпаки, частинки більших розмірів потребують менше води для такого переходу. Безумовно, стан грунту визначається, крім його вологості, ще й мінералогічним складом. Даний підхід цього не враховує, але відповідає основним потребам будівельної практики.
За числом пластичності глинисті грунти розділяються на супіски – 1 ≤ IL ≤ 7, суглинки – 7 < IL ≤ 17 і глини – IL > 17.
 5. Консистенція глинистих грунтів. З підвищенням вологості тіста глинистих грунтів воно переходить у пластичний стан, а потім у текучий. При цьому знижується міцність грунтів. Знаючи природну вологість грунту, а також вологості на межі розкочування і текучості можна оцінити стан, в якому знаходиться грунт. На практиці для визначення стану глинистих грунтів використовують показник текучості
5. Консистенція глинистих грунтів. З підвищенням вологості тіста глинистих грунтів воно переходить у пластичний стан, а потім у текучий. При цьому знижується міцність грунтів. Знаючи природну вологість грунту, а також вологості на межі розкочування і текучості можна оцінити стан, в якому знаходиться грунт. На практиці для визначення стану глинистих грунтів використовують показник текучості 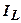
 (2.19)
(2.19)
Глинисті грунти залежно від 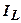 мають слідуючі стани (табл. 2.3).
мають слідуючі стани (табл. 2.3).
6. Класифікація грунтів. Повна класифікація грунтів наводиться в ДСТУ Б В.2.1-2-96 “Грунти. Класифікація” [16]. Згідно стандарту всі грунти розділяються на класи, групи, підгрупи, типи, види і різновиди.
К л а с и - за загальним характером структурних зв’язків. Це природні скельні, дисперсні, мерзлі, техногенні грунти.
Г р у п и - за характером структурних зв’язків з урахуванням їх міцності. Клас скельних грунтів розділяють на скельні та напівскельні, дисперсних - на зв’язні та незв’язні.
П і д г р у п и - за походженням та умовами утворення. Скельні грунти відносять до магматичних, метаморфічних та осадових підгруп; дисперсні - до осадової підгрупи.
Т и п - за речовинним складом. Дисперсні розділяються на мінеральні, органомінеральні та органічні.
В и д - за найменуванням грунтів з урахуванням розмірів частинок та показників властивостей. Мінеральні грунти розділяють на великоуламкові, піски і глинисті грунти; органомінеральні - на мули, сапропелі та заторфовані грунти; органічні - на торфи.
Р і з н о в и д и - за кількісними показниками речовинного складу, властивостей та структури грунтів. Великоуламкові грунти та піски розділяються згідно табл. 2.2; глинисті грунти та мули - за числом пластичності (див. п. 2.4) і за показником текучості (див. табл. 2.3); великоуламкові грунти та піски - за коефіцієнтом водонасичення (див. п. 2.3); піски - за щільністю складу 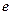 (див. п.2.3) та інше.
(див. п.2.3) та інше.
 Тема 3. ОПІР ГРУНТІВ ЗСУВУ
Тема 3. ОПІР ГРУНТІВ ЗСУВУ
Розглянемо споруду, яка розміщена поблизу укосу і сприймає горизонтальні й вертикальні навантаження (рис. 3.1). В даному випадку несуча здатність грунту може бути вичерпана в результаті втрати стійкості укосу (лінія 1), площинного зсуву фундаменту (лінія 2) чи випирання грунту з-під підошви фундаменту (лінія 3).
 В усіх випадках втрата несучої здатності відбуває-ться шляхом зсуву однієї частини грунту (споруди) відносно іншої, нерухомої частини. Міцність грунту буде тим більшою, чим більший його опір зсуву, тобто чим більшими будуть коефіцієнт тертя і зчеплення між окремими частинками грунту.
В усіх випадках втрата несучої здатності відбуває-ться шляхом зсуву однієї частини грунту (споруди) відносно іншої, нерухомої частини. Міцність грунту буде тим більшою, чим більший його опір зсуву, тобто чим більшими будуть коефіцієнт тертя і зчеплення між окремими частинками грунту.
1. Опір грунтів зсуву. Опір зсуву в лабораторних умовах найчастіше визначають за допомогою одноплощинних зсувних приладів, основною частиною яких є зрізувач (рис. 3.2).
Випробування виконують таким чином. У спеціальних приладах (ущільнювачах) попередньо ущільнюють зразки грунту під тиском, при якому вони будуть випробуватись на зсув (наприклад, 0,1; 0,2; 0,3 мПа). Потім переносять один зразок у зрізувач, прикладають вертикальне навантаження, яке створює нормальний тиск, при якому ущільнюва-вся зразок грунту в ущільнювачі (наприклад, р 1 = 0,1 мПа → р = N / A, де A – площа поперечного перерізу зразка грунту) і окремими ступенями передають на рухому обойму горизонтальні навантаження до моменту, коли відбудеться зсув. Кожний ступінь витримується до умовної стабілізації, при якій горизонтальне переміщення верхньої (рухомої) частини зразка не перевищує 0,01 мм за останні 2 хв. спостережень.
 Залежність між дотичними (зсувними) напруженнями
Залежність між дотичними (зсувними) напруженнями  (τ = Q / A) у зразках і їх переміщенням
(τ = Q / A) у зразках і їх переміщенням  буде мати вигляд, показаний на рис. 3.3.
буде мати вигляд, показаний на рис. 3.3.
За результатами дослідів будують графік. На осі абсцис наносять нормальні напруження  , а на осі ординат - відповідні їм значення граничних зсувних напружень
, а на осі ординат - відповідні їм значення граничних зсувних напружень  (рис. 3.4, чи 3.5).
(рис. 3.4, чи 3.5).
Для графіків відповідно можна записати
 (3.1)
(3.1)
 , де (3.2)
, де (3.2)
 - коефіцієнт внутрішнього тертя;
- коефіцієнт внутрішнього тертя; 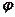 - кут внутрішнього тертя;
- кут внутрішнього тертя;  - питоме зчеплення (викликане структурними зв’язками грунту).
- питоме зчеплення (викликане структурними зв’язками грунту).
 Ці залежності виражають закони Кулона для сипких і зв’язних грунтів. Величини
Ці залежності виражають закони Кулона для сипких і зв’язних грунтів. Величини 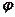 і
і  називаються характеристиками міцності грунтів. Вирази (3.1) і (3.2) справедливі для граничного стану грунту, тобто стану, при якому він вичерпує свою міцність, і в області невеликих нормальних напружень (до 0,6 мПа).
називаються характеристиками міцності грунтів. Вирази (3.1) і (3.2) справедливі для граничного стану грунту, тобто стану, при якому він вичерпує свою міцність, і в області невеликих нормальних напружень (до 0,6 мПа).
Якщо лінію залежності  провести до перетину з віссю абсцис, одержимо значення
провести до перетину з віссю абсцис, одержимо значення  - фіктивний тиск зв‘язності. З рис. 3.5 видно, що
- фіктивний тиск зв‘язності. З рис. 3.5 видно, що
 (3.3)
(3.3)
Методика випробувань викладена в [17].
 2. Ефективний і нейтральний тиск. Описані вище досліди називаються консолідовано-дренованими, тому що грунт попередньо ущільнюється (консолідується) і при цьому надається можливість фільтрації (дренажу) води через отвори в штампі. Якщо випробування на зсув виконувати без попереднього ущільнення і без надання можливості фільтрації води із зразка, то такі досліди називаються неконсолідовано-недренованими. Вони моделюють роботу водонасичених глинистих грунтів в основі фундаментів. При цьому частина напруження буде сприйматися грунтовою водою і закон Кулона прийме такий вигляд
2. Ефективний і нейтральний тиск. Описані вище досліди називаються консолідовано-дренованими, тому що грунт попередньо ущільнюється (консолідується) і при цьому надається можливість фільтрації (дренажу) води через отвори в штампі. Якщо випробування на зсув виконувати без попереднього ущільнення і без надання можливості фільтрації води із зразка, то такі досліди називаються неконсолідовано-недренованими. Вони моделюють роботу водонасичених глинистих грунтів в основі фундаментів. При цьому частина напруження буде сприйматися грунтовою водою і закон Кулона прийме такий вигляд
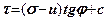 , де (3.4)
, де (3.4)
 - напруження, які сприймає вода.
- напруження, які сприймає вода.
Як видно із (3.4), опір зсуву, а відповідно і міцність водонасичених глинистих грунтів зменшується за рахунок порових напружень. У водонасичених пісках процес консолідації відбувається дуже швидко і всі напруження сприймаються грунтовими частинками (скелетом).
Для кращого розуміння процесу ущільнення грунту в часі розглянемо механічну модель грунтової маси (всі пори грунту повністю заповнені водою - п.1.2). В циліндричній посудині, яка має поршень з мікроскопічними отворами, розміщені пружина і вода (рис. 3.6). Пружина моделює роботу скелета грунту. Зразу ж після передачі тиску 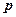 на поршень вся його величина буде сприйматись тільки водою
на поршень вся його величина буде сприйматись тільки водою 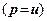
 - нейтральні напруження (тиск). У процесі витіснення води через отвори частина тиску буде поступово сприйматися пружиною
- нейтральні напруження (тиск). У процесі витіснення води через отвори частина тиску буде поступово сприйматися пружиною 
 - ефективні напруження (тиск). Після повного стиснення пружини на останню буде передаватись вся величина тиску
- ефективні напруження (тиск). Після повного стиснення пружини на останню буде передаватись вся величина тиску 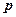
 . Отже, у водонасичених глинистих грунтах напруження буде сприйматися скелетом тільки після повної консолідації таких грунтів.
. Отже, у водонасичених глинистих грунтах напруження буде сприйматися скелетом тільки після повної консолідації таких грунтів.
Механічна модель (рис. 3.6) демонструє, що в процесі ущільнення грунту в ньому одночасно діють дві системи тисків: тиск в скелеті грунту - ефективний, і тиск в поровій воді - нейтральний. Ефективний тиск характеризує напружений стан скелета грунту. Під цим тиском грунт уже деформувався, тобто ущільнився і зміцнився. Отже, такий тиск позитивно впливає на стан грунту. Нейтральний тиск не впливає на напружений стан скелета повністю водонасченого грунту, тотбо він нейтральний у відношенні до скелета грунту.
 3. Стабілометричні випробування. Випробування грунтів роз-глянутим вище методом одноплощинного зсуву не відповідає складному напруженому стану грунтів при дії зовнішніх навантажень від фундаментів будівель і споруд, тому останнім часом для визначення характеристик міцності використовують випробування на трьохосьове стиснення. Схема приладу на трьохосьове стиснення (стабілометра) показана на рис. 3.7. Циліндричний зразок грунту 1 в гумовій оболонці піддають всесторонньому стиненню рідиною 2 інтенсивністю
3. Стабілометричні випробування. Випробування грунтів роз-глянутим вище методом одноплощинного зсуву не відповідає складному напруженому стану грунтів при дії зовнішніх навантажень від фундаментів будівель і споруд, тому останнім часом для визначення характеристик міцності використовують випробування на трьохосьове стиснення. Схема приладу на трьохосьове стиснення (стабілометра) показана на рис. 3.7. Циліндричний зразок грунту 1 в гумовій оболонці піддають всесторонньому стиненню рідиною 2 інтенсивністю  . Потім через шток 3 до поршня 4 прикладають вертикальне навантаження
. Потім через шток 3 до поршня 4 прикладають вертикальне навантаження  , створюючи на зразок вертикальний тиск
, створюючи на зразок вертикальний тиск 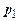 (після сумування з
(після сумування з  ). Збільшуючи тиск
). Збільшуючи тиск 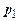 можна досягти повного руйнування зразка грунту або значного його розширення.
можна досягти повного руйнування зразка грунту або значного його розширення.
 Для визначення характеристик міцності сипких грунтів достатньо виконати одне випробування і побудувати коло Мора, діаметр якого дорівнює
Для визначення характеристик міцності сипких грунтів достатньо виконати одне випробування і побудувати коло Мора, діаметр якого дорівнює 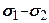 . Дотична до кола Мора 0М, проведена через початок координат, визначить кут внутрішнього тертя
. Дотична до кола Мора 0М, проведена через початок координат, визначить кут внутрішнього тертя 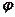 (рис. 3.8). Аналітичний вираз для визначення
(рис. 3.8). Аналітичний вираз для визначення 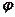 має вигляд
має вигляд
 (3.5)
(3.5)
 Для зв‘язних грунтів виконується два випробування при різних значеннях
Для зв‘язних грунтів виконується два випробування при різних значеннях 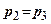 . Потім будують два кола Мора (рис. 3.9), дотична до яких і визначить кут внутрі-шнього тертя
. Потім будують два кола Мора (рис. 3.9), дотична до яких і визначить кут внутрі-шнього тертя 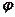 й питоме зчеплення грунту
й питоме зчеплення грунту  . Ана-літичні вирази для визначення
. Ана-літичні вирази для визначення 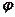 та
та  мають вигляд
мають вигляд
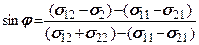 (3.6)
(3.6)
 (3.7)
(3.7)
Методика випробувань викладена в [13].
Кут внутрішнього тертя і питоме зчеплення визначають на основі не менше 18 дослідів. У цьому випадку коефіцієнти  і
і  рівняння (3.2) можуть бути підібрані методом найменших квадратів (див. п. 9.3).
рівняння (3.2) можуть бути підібрані методом найменших квадратів (див. п. 9.3).
Тема 4. Модуль ДЕФОРМАЦІЇ ГРУНТІВ
1. Компресійні дослідження. Для визначення деформації грунтів необхідно знати коефіцієнт пропорційності між деформаціями і напруженнями - модуль деформації. Модуль деформації поширених, відносно однорідних матеріалів (бетон, метал) наводиться в довідниках. Природні ж грунти за своїми механічними властивостями є дуже різноманітними. Тому, зазвичай, перед розрахунками грунтових основ виконують дослідне визначення модуля деформації. Модуль деформації, в основному, визначають за результатами компресійних, cтабілометричних і штампових випробувань або за таблицями будівельних норм СНиП 2.02.01-83 [24].
Оскільки грунт складається з твердих частинок і пор (частково чи повністю заповнених водою і повітрям), то теоретично при його стисненні повинні зменшуватись об‘єми всіх компонентів. Оскільки напруження стиснення, які зазвичай виникають в основах фундаментів, при дії навантажень від надземних конструкцій, порівняно незначні, об‘ємні деформації твердих частинок незрівнянно малі і до уваги не беруться. Отже, можна вважати, що зміна об‘єму грунту при стисненні відбувається лише за рахунок зміни об‘єму пор, яка може відбуватися внаслідок взаємного переміщення окремих частинок в результаті руйнування структурних зв‘язків груту з витісненням повітря і води.
 В лабораторних умовах модуль деформації визначають за допомогою копресійного приладу, основною частиною якого є одометр. Це кругла обойма 1 з днищем 2 (рис.4.1.). Грунт 3 розміщується в кільці 4. Навантаження N передається через штамп 5. Фільтрація води проходить через отвори, які є в днищі і штампі. Деформації грунту вимірюють індикаторами 6.
В лабораторних умовах модуль деформації визначають за допомогою копресійного приладу, основною частиною якого є одометр. Це кругла обойма 1 з днищем 2 (рис.4.1.). Грунт 3 розміщується в кільці 4. Навантаження N передається через штамп 5. Фільтрація води проходить через отвори, які є в днищі і штампі. Деформації грунту вимірюють індикаторами 6.
Оскільки зразок грунту в кільці не має можливості бічного розширення, то зміну його пористості  (відношення об‘єму пор до об‘єму грунту (2.8)) під тиском
(відношення об‘єму пор до об‘єму грунту (2.8)) під тиском  , розподіленим по площі
, розподіленим по площі  , знайдемо з виразу
, знайдемо з виразу
 , де (4.1)
, де (4.1)
 - початкова висота зразка;
- початкова висота зразка;  - деформація зразка від тиску
- деформація зразка від тиску  . Об‘єм твердих частинок до і після деформації незмінний (наше припущення), тому об‘єм твердих частинок в одиниці об‘єму зразка дорівнюватиме (2.9)
. Об‘єм твердих частинок до і після деформації незмінний (наше припущення), тому об‘єм твердих частинок в одиниці об‘єму зразка дорівнюватиме (2.9)
 , де (4.2)
, де (4.2)
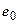 - початковий коефіцієнт пористості грунту.
- початковий коефіцієнт пористості грунту.
Згідно з (2.10)  . Поділивши вираз (4.1) на (4.2), одержимо вираз для визначення зміни коефіцієнта пористості грунту
. Поділивши вираз (4.1) на (4.2), одержимо вираз для визначення зміни коефіцієнта пористості грунту  під дією тиску
під дією тиску 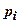

 (4.3)
(4.3)
Урахувавши  для
для  одержимо остаточний вираз для коефіцієнта пористості при дії тиску
одержимо остаточний вираз для коефіцієнта пористості при дії тиску 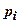
 (4.4)
(4.4)
Після визначення значень  при різних тисках
при різних тисках 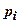 будують залежність
будують залежність  , що має назву компресійної кривої (рис. 4.2).
, що має назву компресійної кривої (рис. 4.2).
При зростанні тиску коефіцієнт пористості зменшується (лінія 1 рис. 4.2). Якщо тиск поступово зменшувати, то зразок частково відновить деформацію і коефіцієнт пористості зросте (лінія 2 рис. 4.2). Первинна висота зразка не буде повністю відновлена, тому що при розвантаженні відновлюються лише пружні деформації.
На початковій ділянці залежність  є лінійною, а деформації незначними. На цій ділянці чинять опір зовнішнім навантаженням структурні зв’язки грунтів. Міцність цих зв’язків називається структурною міцністю
є лінійною, а деформації незначними. На цій ділянці чинять опір зовнішнім навантаженням структурні зв’язки грунтів. Міцність цих зв’язків називається структурною міцністю 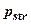 .
.
 Якщо обмежитись незначною зміною тиску р=0,1…0,5 мПа (реальний тиск, який може виникати в основах споруд), то компресійну криву можна замінити прямою лінією АВ (рис.4.3)
Якщо обмежитись незначною зміною тиску р=0,1…0,5 мПа (реальний тиск, який може виникати в основах споруд), то компресійну криву можна замінити прямою лінією АВ (рис.4.3)
Тангенс кута нахилу цієї прямої до осі тисків називається коефіцієнтом стисливості 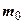
 , де (4.5)
, де (4.5)
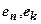 - коефіцієнти пористості відповідно при початковому
- коефіцієнти пористості відповідно при початковому  і кінцевому
і кінцевому  тиску.
тиску.
З певним (доволі суттєвим) наближенням можна записати рівняння компресійної кривої у такому вигляді
 (4.6)
(4.6)
Модуль деформації грунту за результатами компресійних дослідів визначають за виразом
 , де (4.7)
, де (4.7)
 - коефіцієнт, що враховує неможливість поперечного розширення грунту в компресійному приладі.
- коефіцієнт, що враховує неможливість поперечного розширення грунту в компресійному приладі.
В компресійному приладі грунт може деформуватись тільки у вертикальному напрямку. Це погано моделює роботу грунту під фундаментами невеликих розмірів (фундаменти більшості будівель), де величина горизонтальних деформацій є суттєвою. Під фундаментами великих розмірів переважають деформації грунту у вертикальному напрямку. Тому модуль деформації, одержаний за результатами компресійних випробувань, широко використвується для проектування гідротехнічних споруд, а в промисловому і цивільному будівництві тільки для споруд III класу капітальності.
З урахуванням вищесказаного модуль деформацій грунтів  , знайдений за результатами компресійних випробувань визначають за формулою
, знайдений за результатами компресійних випробувань визначають за формулою
 , де (4.8)
, де (4.8)
 - поправочний коефіцієнт (див. п.4.3 останній обзац).
- поправочний коефіцієнт (див. п.4.3 останній обзац).
Методика випробувань викладена в [17].
2. Стабілометричні випробування. Особливістю випробувань на трьохосьове стиснення в стабілометрі є можливість одночасного визначення характеристик стисливості і міцності.
 Модуль деформації за результатами стабілометричних випробувань визначають для довільної точки в межах ділянки пропорційності ОА (рис. 4.4) за формулою
Модуль деформації за результатами стабілометричних випробувань визначають для довільної точки в межах ділянки пропорційності ОА (рис. 4.4) за формулою
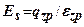 , де (4.9)
, де (4.9)
 - величина бічних стискуючих напружень (девіатор напружень) визначається з виразу
- величина бічних стискуючих напружень (девіатор напружень) визначається з виразу
 , де (4.10)
, де (4.10)
 - загальна величина головного напруження (після сумування з
- загальна величина головного напруження (після сумування з 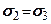 );
);
 , де (4.11)
, де (4.11)
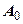 - початкова площа поперечного перерізу зразка;
- початкова площа поперечного перерізу зразка;  - площа поперечного перерізу зразка при дії напруження
- площа поперечного перерізу зразка при дії напруження  ;
;
 , де (4.12)
, де (4.12)
 - вертикальна деформація зразка при напруженні
- вертикальна деформація зразка при напруженні  ;
;  - початкова висота зразка.
- початкова висота зразка.
Методика випробувань викладена в [13].
3. Метод штампових випробувань є еталонним, тобто найбільш точним. Його суть полягає в наступному. На жорсткий круглий штамп окремими ступенями передають навантаження і визначають при цьому його осідання. Кожний ступінь витримують до моменту умовної стабілізації, при якій переміщення штампа не повинні перевищувати 0,1 мм за останні 0,5; 1,0 або 2 год. залежно від грунту. Випробування можуть виконуватись у свердловинах, шурфах або котлованах. Площа штампа залежить від місця випробування (свердловина, котлован) і змінюється від 600 до 10000 см2. Навантаження передають гідродомкратами або тарованими вантажами. На рис. 4.5 наведена найпоширеніша схема штампових випробувань.
Методика випробувань наведена в [2].
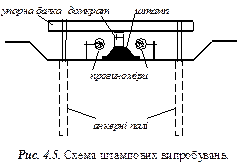 За результатами дослідів будують графік залежності осідань штампа
За результатами дослідів будують графік залежності осідань штампа  від тиску по його підошві
від тиску по його підошві 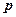 (рис. 4.6).
(рис. 4.6).
Модуль деформації визначають за формулою

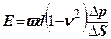 , де (4.13)
, де (4.13)
 - безрозмірний коефіцієнт;
- безрозмірний коефіцієнт; 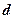 - діаметр штампа;
- діаметр штампа;  - зміна тиску на лінійній ділянці;
- зміна тиску на лінійній ділянці;  - приріст деформації в інтервалі
- приріст деформації в інтервалі  ;
;  - коефіцієнт Пуассона.
- коефіцієнт Пуассона.
!!! Поправочний коефіцієнт  у виразі (4.8) отримано на основі порівняльного аналізу компресійних і штампових визначень модуля деформації грунту.
у виразі (4.8) отримано на основі порівняльного аналізу компресійних і штампових визначень модуля деформації грунту.
Тема 5. ВОДОПРОНИКНІСТЬ ГРУНТУ
Під час проектування водозниження, осушення та водопостачання треба знати скільки води надходить до різних водозабірних споруд (колодязів, свердловин, канав, будівельних котлованів). Приплив води до водозабірних споруд обчислюють з урахуванням характеру її руху (ламінарний або турбулентний) у водоносному шарі, гідравлічних умов (води ненапірні або напірні) та особливостей обладнання водозабірної споруди.
Підземні води, як правило, перебувають у русі (рухаються в порах, тріщинах та розломах грунтів). Рух води в тріщинах та розломах - швидкий, турбулентний. Рух води в порах гірських порід можна розглядати як спокійний, ламінарний. Цей рух одержав назву фільтрації.
1. Коефіцієнт фільтрації. Фільтрація має певну закономірність, яка була вперше встановлена французьким інженером А. Дарсі в 1856 p. Дарсі сконструював прилад для вивчення водопроникності пісків (рис. 5.1). З допомогою цього приладу він одержав таку залежність

 , де (5.1)
, де (5.1)
 - об'єм профільтрованої води;
- об'єм профільтрованої води;  - коефіцієнт пропорційності, який залежить від виду грунту;
- коефіцієнт пропорційності, який залежить від виду грунту;  - площа фільтрації;
- площа фільтрації;  - час фільтрації;
- час фільтрації;  - гідравлічний градієнт
- гідравлічний градієнт
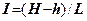 , де (5.2)
, де (5.2)
 - напір води в колбі;
- напір води в колбі;  - напір води в посудині;
- напір води в посудині;  - довжина шляху фільтрації.
- довжина шляху фільтрації.
Розділивши ліву та праву частини виразу (5.1) на  , одержимо об'єм води, що фільтрується за одиницю часу через одиницю площі
, одержимо об'єм води, що фільтрується за одиницю часу через одиницю площі 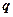
 (5.3)
(5.3)
Об‘єм профільтрованої води буде тим більшим, чим більша її швидкість при фіксованих значеннях решти параметрів. Тому величину 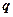 можна назвати швидкісю фільтрації і вимірювати одиницями швидкості (см/с, м/доб). Оскільки швидкість, зазвичай, позначають буквою
можна назвати швидкісю фільтрації і вимірювати одиницями швидкості (см/с, м/доб). Оскільки швидкість, зазвичай, позначають буквою  , то можна записати
, то можна записати
 (5.4)
(5.4)
 у виразі (5.4) прийнято називати коефіцієнтом фільтрації. Він є характеристикою водопроникності порід. Коефіцієнт фільтрації входить у розрахункові формули для визначення припливу води до різноманітних водозабірних споруд, а також у формули для розрахунку деформацій основ будівель і споруд в часі.
у виразі (5.4) прийнято називати коефіцієнтом фільтрації. Він є характеристикою водопроникності порід. Коефіцієнт фільтрації входить у розрахункові формули для визначення припливу води до різноманітних водозабірних споруд, а також у формули для розрахунку деформацій основ будівель і споруд в часі.
В лабораторних умовах коефіцієнт фільтрації визначається з допомогою різних приладів. Такі прилади принципово нічим не відрізняються від приладу Дарсі (наприклад, універсальна трубка). Коефіцієнт фільтрації, (м/доб), при заданій температурі визначають за формулою
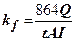 , де (5.5)
, де (5.5)
864 - коефіцієнт для переведення одиниць см/с в м/доб;  - об'єм профільтрованої води, см3;
- об'єм профільтрованої води, см3;  - час фільтрації, с;
- час фільтрації, с;  - площа поперечного перерізу трубки, см2;
- площа поперечного перерізу трубки, см2;  - гідравлічний градієнт.
- гідравлічний градієнт.
Величини  та
та  є параметрами приладу, отже, дослід зводиться до визначення часу
є параметрами приладу, отже, дослід зводиться до визначення часу  , протягом якого профільтрується об'єм води
, протягом якого профільтрується об'єм води  .
.
Методика випробувань викладена в [12].
Найточніше коефіцієнт фільтрації можна визначити шляхом проведення дослідних відкачувань води в польових умовах.
 2. Початковий градієнт напору. Великоуламкові і піщані грунти мають великий
2. Початковий градієнт напору. Великоуламкові і піщані грунти мають великий  супіски менший, суглинки ще менший, а глини взагалі є водоупорами. Чому це так?! Рух води в грунті відбувається по закону ламінарної фільтрації (крива 1 на рис. 5.2), коли грунт містить вільну воду в порах (великоуламкові і піщані грунти), більша частина яких з‘єднана одна з одною. В щільному пилувато-глинистому грунті, в порах якого нема вільної води (вона перебуває в грунті переважно у вигляді гідратних оболонок зв‘язаної води, які окружають частинки грунту), або якщо є, то знаходиться в роз‘єднаних між собою порах, фільтрація води починаєтся лише при градієнті, який більший деякого значения, необхідного для подолання опору водно-колоїдних плівнок її рухові. В такому випадку залежність між градієнтом і швидкістю фільтрації буде мати вигляд кривої 2, зображенної на рис. 5.2. На цій кривій можна виділити дві основні ділянки: криволінійна АВ, яка відповідає переходу від момента виникнення фільтрації до момента розвитку постійної фільтрації, і ділянку постійної фільтрації ВС.
супіски менший, суглинки ще менший, а глини взагалі є водоупорами. Чому це так?! Рух води в грунті відбувається по закону ламінарної фільтрації (крива 1 на рис. 5.2), коли грунт містить вільну воду в порах (великоуламкові і піщані грунти), більша частина яких з‘єднана одна з одною. В щільному пилувато-глинистому грунті, в порах якого нема вільної води (вона перебуває в грунті переважно у вигляді гідратних оболонок зв‘язаної води, які окружають частинки грунту), або якщо є, то знаходиться в роз‘єднаних між собою порах, фільтрація води починаєтся лише при градієнті, який більший деякого значения, необхідного для подолання опору водно-колоїдних плівнок її рухові. В такому випадку залежність між градієнтом і швидкістю фільтрації буде мати вигляд кривої 2, зображенної на рис. 5.2. На цій кривій можна виділити дві основні ділянки: криволінійна АВ, яка відповідає переходу від момента виникнення фільтрації до момента розвитку постійної фільтрації, і ділянку постійної фільтрації ВС.
Для ділянки ВС швидкість фільтрації знаходять за виразом
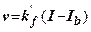 , де (5.6)
, де (5.6)
 - коефіцієнт фільтрації на відрізку АВ;
- коефіцієнт фільтрації на відрізку АВ;  - початковий градієнт напору.
- початковий градієнт напору.
Тема 6. ОСОБЛИВОСТІ ФІЗИКО-МЕХАНІЧНИХ ХАРАКТЕРИСТИК СТРУКТУРНО-НЕСТІЙКИХ і деяких особливих ГРУНТІВ
До структурно-нестійких належать такі грунти, які під дією певних факторів можуть змінювати свої фізико-механічні характеристики і різко деформуватись:
лесові - структура їх різко порушується при замочуванні;
мерзлі - структура їх різко порушується при відтаненні;
пухкі піски - різко ущільнюються при дії динамічних навантажень;
мули і чутливі глини - деформаційні і міцнісні характеристики різко зменшуються при порушенні їх природної структури.
До особливих грунтів відносяться:
набухаючі - при зволоженні суттєво збільшуються в об‘ємі, а при висиханні - зменшуються;
торфи і заторфовані грунти - мають значну стисливість і малу міцність.
1. Просідаючі грунти та їх властивості. Просідаючими називаються глинисті грунти, які під дією зовнішнього навантаження або (і) власної ваги при замочуванні водою чи розчинами дають додаткове осідання, що називається просіданням і відносне просідання для яких  .
.
Властивості просідання мають леси та лесовидні супіски і суглинки. Леси мають у своєму складі понад 50% пилуватих частинок, легкорозчинні солі та пори великих розмірів. При замочуванні структурних зв’язків, які утворені при участі розчинних солей, вони (зв‘язки) руйнуються, частинки ущільнюються, заповнюючи вільні пори, об’єм грунту зменшується, тобто відбувається його просідання.
Просідаючі грунти займають понад 80% території України і розповсюджені на всій площі за винятком Полісся, Карпат, південної частини Криму та західної частини Одеської області. Найбільшої товщини лесові відкладення досягають в південних та східних регіонах. У південній частині Рівненської області розповсюджені лесовидні супіски і суглинки товщиною, переважно, до 5 м. Лесові та лесовидні грунти завжди залягають безпосередньо під рослинним шаром, проте можуть бути й похованими (розміщуватись під насипним шаром).
 В природному стані просідаючі грунти мають низьку вологість та високу міцність. При замочуванні цей грунт легко розмокає зменшуючись в об‘ємі.
В природному стані просідаючі грунти мають низьку вологість та високу міцність. При замочуванні цей грунт легко розмокає зменшуючись в об‘ємі.
Відносне просідання найчастіше визначають в компресійних приладах.
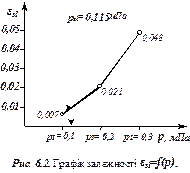 Випробування виконують за методами однієї чи двох кривих. У першому випадку на зразок висотою
Випробування виконують за методами однієї чи двох кривих. У першому випадку на зразок висотою  (рис. 6.1) передають тиск, що відповідає природнному напруженню
(рис. 6.1) передають тиск, що відповідає природнному напруженню  , після цього висота зразка складе
, після цього висота зразка складе  . Потім збільшують тиск до величини
. Потім збільшують тиск до величини  і висота зразка зменшиться до величини
і висота зразка зменшиться до величини  . Після замочування відбудеться просідання грунту і його висота стане рівною
. Після замочування відбудеться просідання грунту і його висота стане рівною  . Відносне просідання грунту
. Відносне просідання грунту  становить
становить
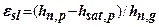 (6.1)
(6.1)
 Таким чином, можна отримати величину
Таким чином, можна отримати величину  , яка відповідає якомусь одному значенню тиску
, яка відповідає якомусь одному значенню тиску 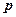 . Із зміною тиску змінюється і відносне просідання. Тому при використанні такої методики проводять декілька дослідів при різних значеннях
. Із зміною тиску змінюється і відносне просідання. Тому при використанні такої методики проводять декілька дослідів при різних значеннях 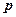 , за результатами яких будують графік залежності
, за результатами яких будують графік залежності  (рис. 6.2).
(рис. 6.2).
Методика випробувань викладена в [9].
Суть методу двох кривих полягає в тому, що в компресійних приладах випробовують зразки грун-ту природної вологості та водонасичені (рис. 6.3). За цими графіками легко можна визначити  при різних тисках
при різних тисках  .
.
Методика випробувань викладена в [9].
Грунти відносять до просідаючих, якщо  . Відповідно, початковим просідаючим називається тиск
. Відповідно, початковим просідаючим називається тиск  , при якому
, при якому  (рис. 6.2).
(рис. 6.2).
2. Набухаючі грунти та їх властивості. До набухаючих відносяться глинисті грунти, які при замочуванні водою чи іншими розчинами збільшуються в об’ємі, причому величина відносного набухання у вільному стані (без навантаження)  (прилад ПНГ). Відносне набухання визначають також при дії тиску, для чого використовують компресійні прилади. Відносне набухання грунтів порушеної структури визначають за виразом (6.2), а непорушеної за виразом (6.3)
(прилад ПНГ). Відносне набухання визначають також при дії тиску, для чого використовують компресійні прилади. Відносне набухання грунтів порушеної структури визначають за виразом (6.2), а непорушеної за виразом (6.3)
 , (6.2)
, (6.2)
 , де (6.3)
, де (6.3)

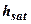 - висота зразка після зволоження (порушеної структури);
- висота зразка після зволоження (порушеної структури);  - початкова висота зразка (порушеної структури);
- початкова висота зразка (порушеної структури);  - висота незамоченого зразка непорушеної структури при дії тиску
- висота незамоченого зразка непорушеної структури при дії тиску  ;
;  - висота незамоченого зразка непорушеної структури при дії тиску
- висота незамоченого зразка непорушеної структури при дії тиску  ;
;  - те ж, замоченого.
- те ж, замоченого.
 залежить від тиску. Найбільші значення відносне набухання має при нульовому тиску. Аналогічно відносному просіданню,
залежить від тиску. Найбільші значення відносне набухання має при нульовому тиску. Аналогічно відносному просіданню,  може визначатись методами однієї або двох кривих.
може визначатись методами однієї або двох кривих.
У першому випадку на зразок висотою  (рис. 6.4) передають тиск, що відповідає природнному напруженню
(рис. 6.4) передають тиск, що відповідає природнному напруженню  , після цього висота зразка складе
, після цього висота зразка складе  . Потім збільшують тиск до величини
. Потім збільшують тиск до величини  і висота зразка зменшиться до величини
і висота зразка зменшиться до величини  . Після замочування відбудеться набухання грунту і його висота стане рівною
. Після замочування відбудеться набухання грунту і його висота стане рівною  . Таким чином можна отримати величину
. Таким чином можна отримати величину  , яка відповідає якомусь одному значенню тиску
, яка відповідає якомусь одному значенню тиску 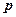 . Тому при використанні такої методики проводять декілька дослідів при різних значеннях
. Тому при використанні такої методики проводять декілька дослідів при різних значеннях 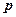 , за результатами яких будують графік залежності
, за результатами яких будують графік залежності  (рис. 6.5).
(рис. 6.5).
Методика випробувань викладена в [11].
 Суть методу двох кривих полягає в тому, що в компресійних приладах випробовують зразки грунту природної вологості та водонасичені (рис. 6.6). За цими графіками легко можна визначити
Суть методу двох кривих полягає в тому, що в компресійних приладах випробовують зразки грунту природної вологості та водонасичені (рис. 6.6). За цими графіками легко можна визначити 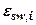 при різних тисках
при різних тисках  .
.
Методика випробувань викладена в [11].
Грунти відносять до набухаючих (при якомусь тиску), якщо  . Відповідно, початковим набухаючим називається тиск
. Відповідно, початковим набухаючим називається тиск  , при якому
, при якому  (рис. 6.5).
(рис. 6.5).
Головну роль у процесі набухання відіграють глинисті частинки. Особливе значення має наявність таких мінералів, як іліт і монтморилоніт. Вода, потрапляючи в такі грунти, здатна розклинювати тверді мінеральні частинки, що призводить до набухання грунту.
Процес набухання має зворотній характер. Якщо сушити грунт після набухання, то виникає усадка – зменшення об‘єму.
Методика випробувань викладена в [11].
На Україні набухаючі грунти розповсюджені переважно в Криму, поблизу міст Керч та Феодосія.
Розділ ІІ. механіка грунтів
Тема 7. ВИЗНАЧЕННЯ НАПРУЖЕНЬ В ГРУНТАХ
 В будь-якій точці грунтового масиву виникає система напружень, спричинена власною вагою вищележачих шарів грунту – природні напруження та прикладеного до поверхні грунтового масиву зовнішнього навантаження – додаткові напруження. Дослідженням встановлено: грунт в більшості випадків не є пружним тілом (залишкові деформації в грунті значно більші від пружних – компресійна крива рис. 4.2); грунту не властива строга лінійна залежність між напруженнями і деформаціями (компресійна крива рис. 4.2). Крім того, в більшості випадків грунт є несуцільним (дисперсним) тілом (п. 1.2). В зв‘язку з цим виникає питання, в яких випадках допустимо використовувати рішення теорії пружності, для визначення напружень в грунтах. Для вияснення цього розглянемо переміщення фундамента від дії статичного навантаження.
В будь-якій точці грунтового масиву виникає система напружень, спричинена власною вагою вищележачих шарів грунту – природні напруження та прикладеного до поверхні грунтового масиву зовнішнього навантаження – додаткові напруження. Дослідженням встановлено: грунт в більшості випадків не є пружним тілом (залишкові деформації в грунті значно більші від пружних – компресійна крива рис. 4.2); грунту не властива строга лінійна залежність між напруженнями і деформаціями (компресійна крива рис. 4.2). Крім того, в більшості випадків грунт є несуцільним (дисперсним) тілом (п. 1.2). В зв‘язку з цим виникає питання, в яких випадках допустимо використовувати рішення теорії пружності, для визначення напружень в грунтах. Для вияснення цього розглянемо переміщення фундамента від дії статичного навантаження.
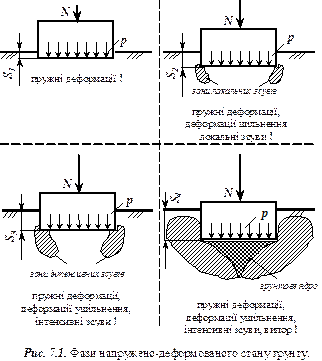
1. Фази напруженого стану грунтів. Нехай на поверхні грунту встановлено жорсткий фундамент (рис. 7.1), завантажений навантаженням  . Під дією цього навантаження в масиві грунту відбуваються переміщення, величина яких буде збільшуватись по мірі збільшення тиску (p=N/A) на грунт основи. Графік залежності осідань фундаменту
. Під дією цього навантаження в масиві грунту відбуваються переміщення, величина яких буде збільшуватись по мірі збільшення тиску (p=N/A) на грунт основи. Графік залежності осідань фундаменту  від тиску
від тиску 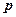 під його підошвою має вигляд (рис. 7.2). На кривій
під його підошвою має вигляд (рис. 7.2). На кривій 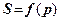 можна виділити чотири ділянки. Перша
можна виділити чотири ділянки. Перша  відповідає навантаженню, при якому напруження, що виникають в грунті під основною частиною фундамента не перевищують структурну міцність грунту
відповідає навантаженню, при якому напруження, що виникають в грунті під основною частиною фундамента не перевищують структурну міцність грунту 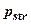 . Цю фазу називають фазою пружних деформацій, хоч одночасно з ними під краями фундаменту, де відбувається концентрація напружень, розвиваються пластичні деформації і деформації ущільнення. Остання обставина призводить до того, що в межах цієї фази між осіданням і тиском немає строгої лінійної залежності.
. Цю фазу називають фазою пружних деформацій, хоч одночасно з ними під краями фундаменту, де відбувається концентрація напружень, розвиваються пластичні деформації і деформації ущільнення. Остання обставина призводить до того, що в межах цієї фази між осіданням і тиском немає строгої лінійної залежності.
 При подальшому збільшенні тиску, внаслідок нерівномірності його розподілу по підошві фундаменту напруження під краями будуть перевищувати структурну міцність. Це призведе до перерозподілу тиску. Коли тиск під всією підошвою фундаменту перевищить структурну міцність грунту, в основі стануть розвиватися деформації ущільнення. При тисках, які незначно перевищують структурну міцність грунту, ущільнення розвивається лише в зоні, яка безпосередньо прилягає до підошви фундамента. По мірі збільшення тиску грунт буде ущільнюватись у все більшій зоні, оскільки в межах все більшого об‘єму напруження будуть перевищувати структурну міцність грунту. Одночасно в грунті під краями фундаменту будуть розвиватися деформації зсувів, поглиблюючи криволінійність ділянки
При подальшому збільшенні тиску, внаслідок нерівномірності його розподілу по підошві фундаменту напруження під краями будуть перевищувати структурну міцність. Це призведе до перерозподілу тиску. Коли тиск під всією підошвою фундаменту перевищить структурну міцність грунту, в основі стануть розвиватися деформації ущільнення. При тисках, які незначно перевищують структурну міцність грунту, ущільнення розвивається лише в зоні, яка безпосередньо прилягає до підошви фундамента. По мірі збільшення тиску грунт буде ущільнюватись у все більшій зоні, оскільки в межах все більшого об‘єму напруження будуть перевищувати структурну міцність грунту. Одночасно в грунті під краями фундаменту будуть розвиватися деформації зсувів, поглиблюючи криволінійність ділянки  . Проте при порівняно незначних тисках (0,1…0,5 мПа), які зазвичай виникають під підошвою фундаментів, криву
. Проте при порівняно незначних тисках (0,1…0,5 мПа), які зазвичай виникають під підошвою фундаментів, криву  можна з деяким наближенням прийняти за пряму. Цю фазу напружено-деформованого стану грунту називають фазою ущільнення. В цій фазі грунт ущільнюється, а його будівельні властивості покращуються (безпосередньо під підошвою фундаменту формується грунтове ядро). Залежність між деформаціями грунту і напруженнями носить приблизно лінійний характер. Для цієї ділянки можна застосувати принцип лінійної деформованості грунтів.
можна з деяким наближенням прийняти за пряму. Цю фазу напружено-деформованого стану грунту називають фазою ущільнення. В цій фазі грунт ущільнюється, а його будівельні властивості покращуються (безпосередньо під підошвою фундаменту формується грунтове ядро). Залежність між деформаціями грунту і напруженнями носить приблизно лінійний характер. Для цієї ділянки можна застосувати принцип лінійної деформованості грунтів.
При подальшому збільшенні тиску зони зсувних деформацій поширюючись в сторони, будуть призводити до ущільнення грунту і по сторонах від цих зон, внаслідок чого вигин кривої на ділянці 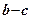 стане більшим. Ця ділянка відповідає значному розвитку локальних зсувів, тому цю фазу напружено-деформованого стану грунту в основі фундаменту називають фазою локальних зсувів. Залежність осідань від тиску на цій ділянці нелінійна.
стане більшим. Ця ділянка відповідає значному розвитку локальних зсувів, тому цю фазу напружено-деформованого стану грунту в основі фундаменту називають фазою локальних зсувів. Залежність осідань від тиску на цій ділянці нелінійна.
При подальшому збільшенні тиску зони локальних зсувів розширюються і в момент, коли досягають ширини фундаменту, відбувається різке осідання фундаменту. На кривій появляться майже вертикальна крива ділянка  , що характеризує цю фазу, яка називається фазою випирання.
, що характеризує цю фазу, яка називається фазою випирання.
Таким чином, четверта фаза абсолютно недопустима для експлуатації будівель і споруд. Вони можуть експлуатуватись в першій і другій фазі (в третій - при умові, що фактичні осідання фундаментів не перевищують їх допустимі значення).
2. Основні припущення. Вище (п. 7.1) було доведена можливість використання в межах двох фаз напружено-деформованого стану (пружних деформацій і локальних зсувів) лінійної залежності між тиском і осіданням фундаменту. Отже, в межах цих фаз грунт вважають лінійно-деформованим тілом.
Внаслідок несуцільності (дисперсності) грунту встановити дійсний напружений стан, який виникає в якій-небудь точці його масиву, з використанням теорії пружності неможливо. Тому обмежуються визначенням середньої інтенсивності напружень в потрібній точці основи, приймаючи умовно, що грунт є суцільним тілом.
Більшість грунтів володіє анізотропією. Проте при рішенні інженерних задач з деяким наближенням приймають, що грунти є ізотропними.
 Розглянемо, як розвиваються деформації грунту в основі фундамента при його розвантаженні. Для цього будемо розвантажувати фундамент після ущільнення грунту основи тиском, який ще не викликав інтенсивних місцевих зсувів. При зменшенні тиску зменшується осідання (крива 2 рис. 7.2). Після повного зняття тиску крива 2 ніколи не повернеться в початок координат, оскільки грунт отримав залишкові деформації. Отже, грунт не є пружним тілом. Внаслідок цього рішення теорії пружності для ізотропних тіл можна використовувати лише при одноразовому завантаженні основи. Оскільки, основи фундаментів зазнають переважно одноразове завантаження (під час спорудження будівлі), то рішення теорії пружності можуть бути використані при вирішенні розглядуваних задач.
Розглянемо, як розвиваються деформації грунту в основі фундамента при його розвантаженні. Для цього будемо розвантажувати фундамент після ущільнення грунту основи тиском, який ще не викликав інтенсивних місцевих зсувів. При зменшенні тиску зменшується осідання (крива 2 рис. 7.2). Після повного зняття тиску крива 2 ніколи не повернеться в початок координат, оскільки грунт отримав залишкові деформації. Отже, грунт не є пружним тілом. Внаслідок цього рішення теорії пружності для ізотропних тіл можна використовувати лише при одноразовому завантаженні основи. Оскільки, основи фундаментів зазнають переважно одноразове завантаження (під час спорудження будівлі), то рішення теорії пружності можуть бути використані при вирішенні розглядуваних задач.
3. Напруження в грунті від дії зосередженого навантаження. Напружений стан у деякій точці простору характеризується сукупністю діючих у ній напружень. В умовах просторової задачі виділяють такі напруження (рис. 7.3).
 Задача по визначенню напружень в ідеальному пружному напівпросторі від дії зосередженої сили, прикладеної на його поверхні, розв’язана в 1885 р. французьким вченим Буссінеском. Розглянемо дію вертикальної зосередженої сили
Задача по визначенню напружень в ідеальному пружному напівпросторі від дії зосередженої сили, прикладеної на його поверхні, розв’язана в 1885 р. французьким вченим Буссінеском. Розглянемо дію вертикальної зосередженої сили  , прикладеної в точці
, прикладеної в точці  до горизонтальної площини, яка є поверхнею лінійно-деформованого напівпростору (рис. 7.4). Від дії сили
до горизонтальної площини, яка є поверхнею лінійно-деформованого напівпростору (рис. 7.4). Від дії сили  у всіх точках напівпростору виникне складний напружено-деформований стан. В загальному випадку в будь-якій точці
у всіх точках напівпростору виникне складний напружено-деформований стан. В загальному випадку в будь-якій точці  напівпростору, дещо віддаленій від точки
напівпростору, дещо віддаленій від точки  , буде діяти шість складових напружень (рис. 7.4. - показано три). Нехай положення точки
, буде діяти шість складових напружень (рис. 7.4. - показано три). Нехай положення точки  (рис. 7.5) визначається полярними координатами
(рис. 7.5) визначається полярними координатами 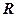 і
і  системи координат з початком в точці прикладання сили
системи координат з початком в точці прикладання сили  . Під дією сили
. Під дією сили  точка
точка  переміститься в напрямку радіуса на величину
переміститься в напрямку радіуса на величину  . Чим далі від місця прикладення сили
. Чим далі від місця прикладення сили  буде
буде  розміщена точка
розміщена точка  , тим меншим буде її переміщення. При
, тим меншим буде її переміщення. При  переміщення точки
переміщення точки  буде дорівнювати нулю. Отже,
буде дорівнювати нулю. Отже,  можна прийняти обернено пропорційним
можна прийняти обернено пропорційним 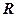 . Одночасно при одному й тому ж значенні
. Одночасно при одному й тому ж значенні 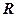 для різних величин кута
для різних величин кута  переміщення точок будуть неоднакові. Найбільше переміщення отримає точка на осі
переміщення точок будуть неоднакові. Найбільше переміщення отримає точка на осі 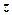 , тобто при
, тобто при  . Із збільшенням кута
. Із збільшенням кута  переміщення в напрямку радіуса зменшуються і у випадку
переміщення в напрямку радіуса зменшуються і у випадку 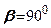 (на поверхні грунту) при малих деформаціях будуть рівними нулю. В зв'язку з цим можна прийняти, що переміщення точки
(на поверхні грунту) при малих деформаціях будуть рівними нулю. В зв'язку з цим можна прийняти, що переміщення точки  у напрямку радіуса (окрім зони біля точки прикладення сили
у напрямку радіуса (окрім зони біля точки прикладення сили  ) буде
) буде
 , де (7.1)
, де (7.1)
 - коефіцієнт пропорційності.
- коефіцієнт пропорційності.
Розглянемо зараз точку  , розміщену на продовженні радіуса
, розміщену на продовженні радіуса 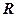 на відстані
на відстані  від точки
від точки  . Керуючись записаним виразом (7.1), переміщення точки
. Керуючись записаним виразом (7.1), переміщення точки  у напрямку радіуса
у напрямку радіуса 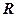 становитиме
становитиме
 (7.2)
(7.2)
Відносна деформація грунту на відрізку  буде
буде
 (7.3)
(7.3)
 Нехтуючи величиною
Нехтуючи величиною  (незрівнянно малою у порівнянні з
(незрівнянно малою у порівнянні з  ) маємо
) маємо
 (7.4)
(7.4)
Згідно з законом Гука, залежність між напруженнями і деформаціями має вигляд  (
( - коефіцієнт пропорційності між напруженнями і деформаціями). Підставивши сюда вираз (7.3) знайдемо залежність для напружень стиснення
- коефіцієнт пропорційності між напруженнями і деформаціями). Підставивши сюда вираз (7.3) знайдемо залежність для напружень стиснення  , які діють на ділянки, перпендикулярні напрямку радіуса
, які діють на ділянки, перпендикулярні напрямку радіуса 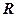
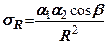 (7.5)
(7.5)
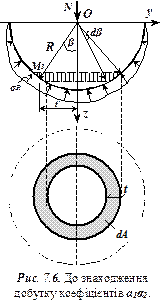
Для знаходження добутку коефіцієнтів 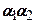 виріжемо умовно частину напівпростору напів-шаровою поверхнею (рис. 7.6), яка має центр в точці
виріжемо умовно частину напівпростору напів-шаровою поверхнею (рис. 7.6), яка має центр в точці  і радіус
і радіус 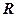 , і складемо рівняння рівноваги проекцій на вісь
, і складемо рівняння рівноваги проекцій на вісь 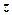 всіх сил, які діють на вирізаний елемент. Отримаємо
всіх сил, які діють на вирізаний елемент. Отримаємо
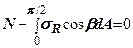 , де (7.6)
, де (7.6)
 - площа кільця напівшарової поверхні при зміні кута
- площа кільця напівшарової поверхні при зміні кута  на величину
на величину  :
:  .
.
Підставляємо в рівняння (7.6) значення для  і
і  з (7.5) одержимо
з (7.5) одержимо
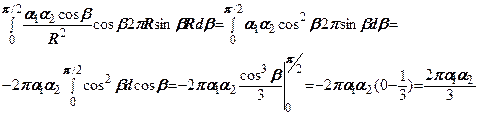
Підставляємо отримане значення у вираз (7.6)
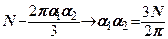
 Підставивши значення
Підставивши значення  у (7.5) отримаємо
у (7.5) отримаємо
 (7.7)
(7.7)
На похилу ділянку  діє тиск
діє тиск  (рівний по величині
(рівний по величині  , але протилежний йому за напрямом) і напруження
, але протилежний йому за напрямом) і напруження 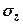 , яке нам потрібно знайти. Розглядаючи рівновагу елементарної трикутної призми (рис. 7.7), складемо рівняння проекцій всіх сил на вертикальну вісь
, яке нам потрібно знайти. Розглядаючи рівновагу елементарної трикутної призми (рис. 7.7), складемо рівняння проекцій всіх сил на вертикальну вісь 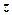
 (7.8)
(7.8)
Перейдемо до декартової системи координат. Оскільки  (рис. 7.5), то
(рис. 7.5), то
 (7.9)
(7.9)
Врахувавши те, що  і підставляємо його у вираз (7.9), матимемо
і підставляємо його у вираз (7.9), матимемо
 (7.10)
(7.10)
Позначимо  - табличний коефіцієнт, тоді
- табличний коефіцієнт, тоді

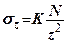 (7.11)
(7.11)
Аналогічним чином можуть бути знайдені решта напружень  .
.
Якщо на поверхні діє декілька сил (рис.7.8), то
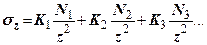 (7.12)
(7.12)
 4. Напруження в грунті від дії розподіленого навантаження. Нехай до поверхні лінійно-деформованого напівпростору в мажах площі
4. Напруження в грунті від дії розподіленого навантаження. Нехай до поверхні лінійно-деформованого напівпростору в мажах площі  прикладено розподілене навантаження змінної в плані інтенсивності (рис. 7.9). Завантажену площу можна розбити на невеличкі прямокутники із сторонами
прикладено розподілене навантаження змінної в плані інтенсивності (рис. 7.9). Завантажену площу можна розбити на невеличкі прямокутники із сторонами  ,
,  і більш складні фігури в межах контуру площі
і більш складні фігури в межах контуру площі  . З деяким наближенням тиск, який розподілено в межах і -го прямокутника можна замінити рівнодіючою
. З деяким наближенням тиск, який розподілено в межах і -го прямокутника можна замінити рівнодіючою  , прикладеною в центрі ваги цього тиску. Вертикальне стискуюче напруження
, прикладеною в центрі ваги цього тиску. Вертикальне стискуюче напруження  в будь-якій точці напівпростору від зосередженої сили можна знайти по аналогії з виразом (7.11)
в будь-якій точці напівпростору від зосередженої сили можна знайти по аналогії з виразом (7.11)
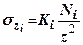
Не нашли, что искали? Воспользуйтесь поиском: