Действия над матрицами

Две матрицы одинакового размера называются равными, если их соответствующие элементы равны.

А = В, если = (i = 1,2,…, m; j = 1,2,…, n).

Суммой двух матриц одинакового размера называется матрица того же размера, все элементы которой равны суммам соответствующих элементов слагаемых матриц.

А + В = С, если + = (i = 1,2,…, m; j = 1,2,…, n).

Пример 1

.

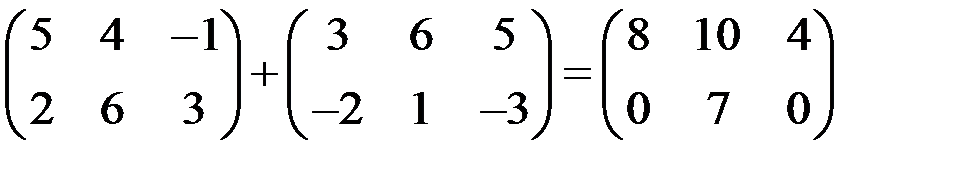Произведением матрицы А на число α называется матрица αА или А α, все элементы которой равны соответствующим элементам матрицы А, умноженным на α.

Пример 2

Матрица 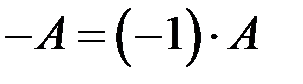называется противоположной матрице А.

Умножение матриц.

Пусть дана матрица А размера m ´ n и матрица В размера n ´ p.

Для двух матриц А и В, у которых число столбцов первой матрицы равно числу строк второй матрицы, определено понятие произведения матрицы А на В следующим образом:

С = А · В, где С есть матрица размера m ´ p,

,

если , где (i = 1,2,…, m; j = 1,2,…, p).

Из определения вытекает следующее правило умножения матриц: чтобы получить элемент, стоящий в i -той строке и j -том столбце произведения двух матриц, нужно элементы i -той строки первой матрицы умножить на соответствующие элементы j –го столбца второй и полученные произведения сложить.

Таким образом, чтобы составить первую строку матрицы С нужно перемножить первую строку матрицы А поочередно на все столбцы В; чтобы получить вторую строку произведения С, нужно вторую строку А перемножить последовательно на все столбцы В и т.д.

Пример 3

Произведение двух матриц НЕ подчиняетсяпереместительному (коммутативному) закону

,

в чем можно убедиться на примерах. Кроме того, если произведение АВ определено, то ВА может не иметь смысла.

В частных случаях, когда матрицы называются перестановочными.

Легко доказать, что единичная матрица Е перестановочна с любой квадратной матрицей А того же порядка, причем

А Е = Е А = А.

Таким образом, единичная матрица играет роль единицы при умножении.

Пример 4

Найти значение матричного многочлена , если , , .

Решение

.

Не нашли, что искали? Воспользуйтесь поиском: