Векторная функция одного скалярного аргумента

Задавая кривую параметрическими уравнениями, мы должны задать три координатных функции, но как известно три координаты кроме точек в пространстве имеют и векторы.

Определение: Если t 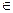(а, b) в соответствие ставится вектор , то говорят, что задана вектор-функция (векторная функция одного скалярного аргумента t).

Для задания вектор-функции необходимо и достаточно задать координатные функции х (t), у (t), z (t).

Т.е. =(х (t); у (t); z (t)) = х (t)· + у (t)· + z (t)· .

Определение: Интервал (а, b) называется областью определения вектор-функции.

Замечание: Область определения может быть замкнутым отрезком, замкнутым слева (справа) или бесконечно-большим.

Если t 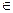(а, b) все векторы поместить в одну точку, тогда концы этих векторов будут образовывать некоторое множество точек в пространстве.

Определение: Если начала всех векторов находятся в начале системы координат, то множество точек – концов этих векторов называется годографом вектор-функции.

Пусть даны несколько вектор-функции и существует хотя бы одна общая точка из их областей определения, тогда для них в этой точке определены все операции, осуществимые для векторов.

Даны вектор-функции =(х₁ (t); у₁ (t); z₁ (t)) и =(х₂ (t); у₂ (t); z₂ (t))

и скалярная функция λ (t), имеющие общую область определения (а, b).

Тогда на (а, b) определены функции:

± =(х₁ (t) ± х₂ (t); у₁ (t) ± у₂ (t); z₁ (t) ± z₂ (t))

λ (t)· =(λ (t)· х₁ (t); λ (t)· у₁ (t); λ (t)· z₁ (t))

· = х₁ (t)· х₂ (t) + у₁ (t)· у₂ (t) + z₁ (t)· z₂ (t)

× =

Замечание: В дальнейшем будем считать, что (а, b) - общая область определения существует, а значит операции с вектор-функциями определены.

Замечание: Если координатные функции являются регулярными, то вектор-функция является регулярной.

Определение: Вектор - называется пределом при t→ t ₀, если

ε > 0, 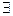δ_ε > 0 такое, что t: | t - t ₀ | < δ_ε | - | < ε.

Обозначение: = или .

Замечание: Если .

Замечание: Для предела вектор-функции справедливы основные теоремы о пределах скалярных функций.

Теорема: Пусть = , = и λ (t) = λ, тогда

± = ± λ (t)· = λ ·

· = · × = ×

Доказательство:

Т.к. = , тогда

ε₁ > 0, 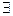δ_ε1 > 0 такое, что t: | t - t ₀ | < δ_{ε 1} | - | < ε₁.

Для = ,

ε₂ > 0, 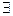δ_ε2 > 0 такое, что t: | t - t ₀ | < δ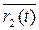_ε2 | - | < ε₂.

Для λ (t) = λ,

ε₃ > 0, 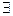δ_ε3 > 0 такое, что t: | t - t ₀ | < δ_ε3 | λ (t) - λ | < ε₃.

1. .

2. =

= .

3.

<

< .

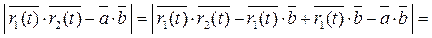
4.

<

< .

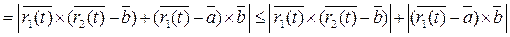При доказательстве мы воспользовались свойствами длины вектора:

,

Задача. Найдите предел вектор-функции при t→ 0.

Решение.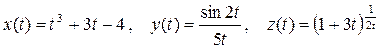

Найдем пределы координатных функций.

=0,4

.

= = (-4; 0,4; ).

Не нашли, что искали? Воспользуйтесь поиском: