
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Производная и дифференциал вектор-функции
Лекция № 2 от 19.02.2014.
Определение: Вектор-функция  называется непрерывной в точке t 0, если при t→ t 0 имеем
называется непрерывной в точке t 0, если при t→ t 0 имеем  →
→  или
или 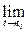
 =
=  .
.
Теорема. Пусть  ,
,  непрерывные вектор-функции и λ (t) – непрерывная скалярная функция в точке t 0, тогда непрерывными в точке t 0 будут функции:
непрерывные вектор-функции и λ (t) – непрерывная скалярная функция в точке t 0, тогда непрерывными в точке t 0 будут функции:  ±
±  , λ (t)·
, λ (t)·  ,
,  ·
·  ,
,  ×
×  .
.
Доказательство. Самостоятельно.
Теорема. Пусть вектор-функция  =(х (t); у (t); z (t)) при t→ t 0 имеет предел
=(х (t); у (t); z (t)) при t→ t 0 имеет предел 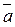 = (а 1; а 2; а 3), тогда
= (а 1; а 2; а 3), тогда 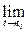 х (t) = а 1,
х (t) = а 1, 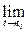 у (t) = а 2,
у (t) = а 2, 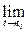 z (t) = а 3.
z (t) = а 3.
Доказательство: Основная идея доказательство заключается в том, что для
того, чтобы 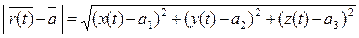 < ε, достаточно,
< ε, достаточно,
чтобы 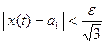 ,
, 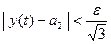 ,
, 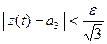 . (Самостоятельно)
. (Самостоятельно)
Определение: Вектор-функция  называется непрерывной на интервале
называется непрерывной на интервале
(а, b), если она непрерывна в каждой точке отрезка.
Производная и дифференциал вектор-функции
Пусть дана непрерывная вектор-функция  =(х (t); у (t); z (t)) или
=(х (t); у (t); z (t)) или  = х (t)·
= х (t)· 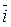 + у (t)·
+ у (t)·  + z (t)·
+ z (t)· 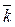 .
.
Обозначим приращение аргумента Δ t = t – t 0, тогда можно рассматривать приращение вектор-функции Δ  =
=  -
-  .
.
Определение: Производной вектор-функции в точке t 0 называется вектор
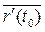 =
= 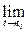
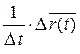 =
= 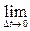
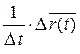 .
.
Замечание: Для удобства, в дальнейшем будем записывать 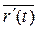 =
= 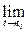
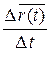
(вектор можно делить на число).
Рисунок
Определение: Если для вектор-функции  в точке t 0 существует производная, то она называется дифференцируемой.
в точке t 0 существует производная, то она называется дифференцируемой.
Пусть вектор-функция  имеет производную в точке t 0 -
имеет производную в точке t 0 - 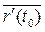 .
.
Рассмотрим вектор 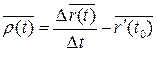
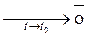 .
.

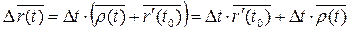
Величину 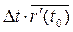 будем называть главной линейной частью приращения вектор-функции (по аналогии со скалярными функциями).
будем называть главной линейной частью приращения вектор-функции (по аналогии со скалярными функциями).
Величина 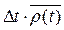 - бесконечно-малая более высокого порядка, чем Δ t.
- бесконечно-малая более высокого порядка, чем Δ t.
Т.о. 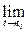
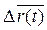 =
= 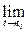
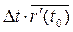 +
+ 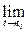
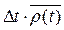 =(
=(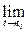
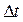 )∙
)∙ 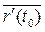 +
+ 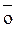
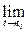
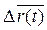 =
=  ,
, 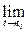
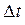 = d t
= d t 
 = dt ∙
= dt ∙ 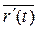 , или
, или
По аналогии с дифференциалом скалярной функции:
 =
= 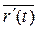 ∙ d t и
∙ d t и 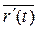 =
= 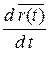 .
.
Не нашли, что искали? Воспользуйтесь поиском: