
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Геометрический смысл производной и дифференциала вектор-функции
Пусть на (a; b) дана вектор-функция  . Рассмотрим
. Рассмотрим  t 1 и t 2
t 1 и t 2  (a, b)
(a, b)
М1=(х 1(t); y 1(t); z 1(t)) 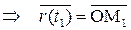 ; М2=(х 2(t); y 2(t); z 2(t))
; М2=(х 2(t); y 2(t); z 2(t)) 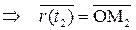 .
.
Δ t = t 2 – t 1, Δ  =
= 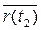 -
- 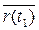 =
=  - вектор секущей.
- вектор секущей.
Следовательно 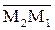 ║
║  Δ
Δ 
Если t 2 → t 1, то точка М2 по кривой приближается к М1, а значит 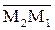 → ō. Так как существует производная отличная от ō, то секущая (М1М2) стремится к своему предельному положению – касательной.
→ ō. Так как существует производная отличная от ō, то секущая (М1М2) стремится к своему предельному положению – касательной.
Направляющий вектор касательной 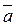 =
= 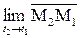 ║
║ 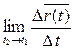 =
= 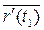
РИСУНОК
Т.о. вектор 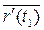 параллелен к касательной в точке М1 - в этом заключается геометрический смысл вектора производной и вектора дифференциала.
параллелен к касательной в точке М1 - в этом заключается геометрический смысл вектора производной и вектора дифференциала.
Тем не менее, │ 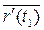 │- не имеет геометрического смысла, т.к. параметризация кривой произвольна. Введя новую параметризацию t = t (τ), получим
│- не имеет геометрического смысла, т.к. параметризация кривой произвольна. Введя новую параметризацию t = t (τ), получим 

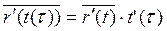 - появился скалярный множитель, но кривая осталась прежней. Т.е. направление вектора осталось, а длина изменилась!
- появился скалярный множитель, но кривая осталась прежней. Т.е. направление вектора осталось, а длина изменилась!
Обозначение: Единичный направляющий вектор касательной будем обозначать 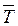
Если производная существует в каждой точке, то она сама является функцией, а значит можно взять производную от производной. Т.о. получится вторая производная 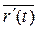 =
=  и т.д.
и т.д.
Определение: п производной вектор-функции называется производная от п -1 производной. 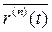 =
= 
Замечание: Для производной вектор-функции справедливы основные теоремы о производных скалярных функций.
Теорема: Пусть для вектор-функций  ,
,  и скалярной функции λ (t) существуют производные, а
и скалярной функции λ (t) существуют производные, а 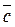 постоянный вектор, тогда
постоянный вектор, тогда
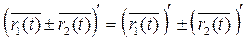


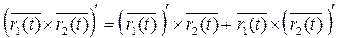
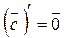

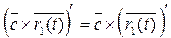
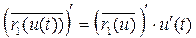
Доказательство: Рассмотрим только одно свойство
 =
=
= 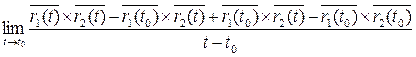 =
=
= 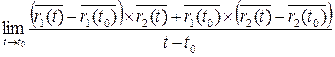 =
=
=  +
+ 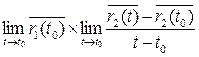 =
=
= 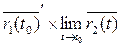 +
+  ==
==  +
+ 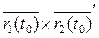
Аналогично доказываются остальные свойства.
Теорема: Если вектор-функция  имеет постоянную длину, тогда её производная перпендикулярна самой вектор-функции.
имеет постоянную длину, тогда её производная перпендикулярна самой вектор-функции.
Доказательство: Пусть  = с, тогда
= с, тогда  ·
·  =
=  = с 2.
= с 2.
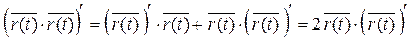
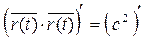 =0
=0 
 =0
=0 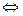
 .
.
Замечание: Это важное свойство вектор-функций мы неоднократно будем применять в дальнейшем.
Задача. Докажите, что касательная к окружности перпендикулярна радиусу, восстановленному в точку касания.
Решение. Уравнение окружности х 2+ у 2= а 2 или х=а ·соs t · · у=а ·sin t,
Или 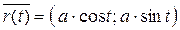 , причем
, причем  = а, тогда по предыдущей теореме, производная вектор-функции (вектор касательной) перпендикулярна самой вектор-функции (радиусу окружности).
= а, тогда по предыдущей теореме, производная вектор-функции (вектор касательной) перпендикулярна самой вектор-функции (радиусу окружности).
Теорема: Для того, чтобы вектор-функция  =(х (t); у (t); z (t)) имела производную необходимо и достаточно, чтобы координатные функции имели производные.
=(х (t); у (t); z (t)) имела производную необходимо и достаточно, чтобы координатные функции имели производные.
Тогда  =(х´ (t); у´ (t); z´ (t)),
=(х´ (t); у´ (t); z´ (t)),  =(х″ (t); у″ (t); z″ (t)) и т.д.
=(х″ (t); у″ (t); z″ (t)) и т.д.
Доказательство: 1. Пусть  = х (t)·
= х (t)· 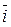 + у (t)·
+ у (t)·  + z (t)·
+ z (t)· 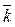 - имеет производную,
- имеет производную,
т.е. 
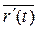 = а 1·
= а 1· 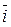 + а 2·
+ а 2·  + а 3·
+ а 3· 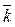 .
.
Координатные функции можно найти следующим образом:
х (t) =  ·
· 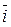 , у (t) =
, у (t) =  ·
·  , z (t)=
, z (t)=  ·
· 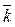 ,
,
а 1 = 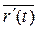 ·
· 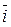 , а 2 =
, а 2 = 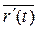 ·
·  , а 3=
, а 3= 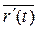 ·
· 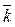 ,
,
Найдем производные координатных функций:
х´ (t)=  у´ (t)=
у´ (t)= 
z´ (t)= 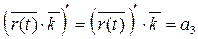
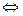
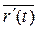 =(х´ (t); у´ (t); z´ (t)).
=(х´ (t); у´ (t); z´ (t)).
2. Пусть х (t), у (t), z (t) - дифференцируемы.
Тогда 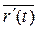 =
= 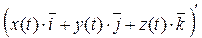 =
=  +
+ 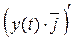 +
+  =
=
= х´ (t)· 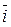 + у´ (t)·
+ у´ (t)·  + z´ (t)·
+ z´ (t)· 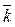 = (х´ (t); у´ (t); z´ (t)).
= (х´ (t); у´ (t); z´ (t)).
Для того, что бы вектор-функция  была k - раз дифференцируема, необходимо и достаточно, что бы координатные функции х (t), у (t), z (t) были дифференцируемы k – раз. В этом случае вектор-функция
была k - раз дифференцируема, необходимо и достаточно, что бы координатные функции х (t), у (t), z (t) были дифференцируемы k – раз. В этом случае вектор-функция  называется регулярной класса k, т.е.
называется регулярной класса k, т.е.  .
.
Задача. Найдите  и
и 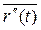 для
для 
Решение. х (t) = а ·соs t, у (t) = а ·sin t, z (t) = b·t
х ′(t) = - а ·sin t, у ′(t) = а ·соs t, z ′(t) = b, тогда 
х ″(t) = - а ·соs t, у ″(t) = - а ·sin t, z ″ (t) = 0 
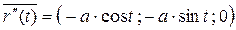
Замечание: Если не оговорено особо, то будем считать, что вектор-функция дифференцируема достаточное число раз (т.е.  ).
).
Для k - раз дифференцируемой вектор-функции  справедливо разложение в ряд Тейлора в окрестности точки t 0:
справедливо разложение в ряд Тейлора в окрестности точки t 0:
 =
=  +
+ 
 +
+ 
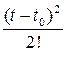 +
+ 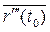
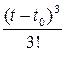 +…+
+…+ 
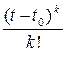 ...
...
Или  =
=  +
+ 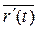
 +
+ 
 +
+ 
 +…+
+…+ 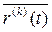
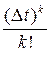 +…
+…
Определение: Если в окрестности точки t 0 вектор-функцию можно разложить в ряд Тейлора, то она называется аналитической.
В каком случае вектор-функция будет задавать элементарную кривую?
Теорема: Пусть х (t), y (t), z (t) дифференцируемые функции, причем
 t
t  (a, b) х ′ 2 + y ′ 2 + z ′ 2 ≠ 0, тогда векторная функция одного скалярного аргумента
(a, b) х ′ 2 + y ′ 2 + z ′ 2 ≠ 0, тогда векторная функция одного скалярного аргумента 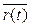 = (х (t); y (t); z (t)) задает некоторую элементарную кривую.
= (х (t); y (t); z (t)) задает некоторую элементарную кривую.
Замечание: Эту теорему можно сформулировать следующим образом: вектор-функция 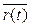 задает элементарную кривую в окрестности точки t 0, если
задает элементарную кривую в окрестности точки t 0, если 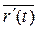 ≠ ō.
≠ ō.
Замечание: Некоторые кривые при подходящем выборе осей координат допускают параметризацию вида 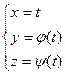 или
или 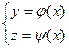 . Это бывает удобнее.
. Это бывает удобнее.
Теорема. Пусть окрестности некоторой точки t 0 регулярная кривая задана уравнениями 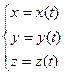 и х ′(t 0) ≠ 0, тогда в достаточно малой окрестности точки t 0, кривая может быть задана уравнениями у= φ (х) z=ψ (х).
и х ′(t 0) ≠ 0, тогда в достаточно малой окрестности точки t 0, кривая может быть задана уравнениями у= φ (х) z=ψ (х).
(без доказательства).
Теорема. Пусть F (х,у,z)=0 и Φ (х,у,z)=0 - регулярные функции от трех переменных (поверхности в E 3) и для некоторой точки М(х 0 ; у 0 ; z0 ) F (х 0, у 0,z0)=0 и Φ (х 0, у 0,z0)=0 (т.е. точка принадлежит поверхностям). Тогда для того чтобы в окрестности этой точки эти уравнения задавали элементарную кривую необходимо и достаточно, чтобы
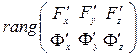 = 2.
= 2.
(без доказательства).
Не нашли, что искали? Воспользуйтесь поиском: