Нормаль и нормальная плоскость

Лекция № 4 от 26.02.14

Угол между кривыми

Рассмотрим две кривые γ₁ и γ₂, пусть они пересекаются в некоторой точке М, которая является обыкновенной для обеих кривых.

Определение: Углом между кривыми будем называть угол между касательными к кривым в общей точке.

Замечание: Если кривые не имеют общей точки, то угол между ними не существует. Если общих точек несколько, то угол можно найти для каждой точки.

Если кривые заданы вектор-функциями 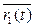=(х₁ (t); y₁ (t); z₁ (t)) и =(х₂ (t); y₂ (t); z₂ (t)) и точка М общая для них, т.е. М(х₁ (t₁); y₁ (t₁); z₁ (t₁)) и М(х₂ (t₂); y₂ (t₂); z₂ (t₂)), тогда угол φ между кривыми в точке М можно найти используя скалярное произведение: соs φ = .

Для случаев, кода кривые заданы не параметрически, сначала необходимо найти направляющий вектор касательной.

Задача. Найти угол между кривыми γ₁: и γ₂: .

Решение. Кривая γ₁ заданная пересечением поверхностей: круговой цилиндр и плоскость, а значит является окружностью.

Возьмем для нее параметризацию: .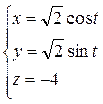

Найдем точки пересечения линий

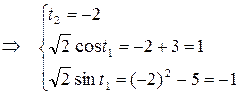
Для первой кривой , для второй .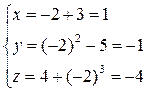

Т.о. точка пересечения кривых М(1; -1; -4).

Найдем векторы касательных к каждой кривой в точке М.

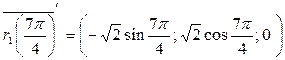= (1; 1; 0)

= (1; -4; 12)

соs φ = = .

Нормаль и нормальная плоскость

Определение: Прямая, проходящая через точку М и перпендикулярная касательной, называется нормалью к кривой в точке М.

Если кривая плоская, то в этой плоскости нормаль единственна. Вектор перпендикулярный касательной (φ′_х; φ′_у), а значит он и является направляющим вектором для нормали уравнение нормали в точке М(х ₀; у ₀)

.

Для кривой, заданной параметрически или вектор-функцией , направляющий вектор касательной =(х´ (t); у´ (t)), для нормали он будет ортогональным уравнение нормали в точке М (х (t ₀); у (t ₀))

.

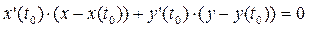Если кривая не плоская, то прямых ортогональных касательной много. Все они лежат в одной плоскости (Почему?)

Определение: Плоскость, перпендикулярная касательной к кривой в точке касания, называется плоскостью нормалей или нормальной плоскостью.

Если регулярная кривая, задана =(х (t); y (t); z (t)) в некоторой точке при значении параметра t ₀ - М(х (t ₀); y (t ₀); z (t ₀)) и =(х' (t ₀); y' (t ₀); z' (t ₀))≠ō

Тогда направляющий вектор касательной к кривой в точке М будет нормальным вектором плоскости. В этом случае уравнение нормальной плоскости имеет вид: х' (t ₀)·(х – х (t ₀)) + y' (t ₀)·(у – у (t ₀)) + z' (t ₀)·(z - z (t ₀)) = 0.

Для случая плоской кривой =(х (t); y (t); 0) и =(х' (t ₀); y' (t ₀); 0)

уравнение нормальной плоскости: х' (t ₀)·(х – х (t ₀)) + y' (t ₀)·(у – у (t ₀)) + 0· z = 0.

Для кривой, заданной пересечением поверхностей 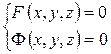в некоторой точке М(х ₀; y ₀; z ₀) и =2, направляющий вектор касательной = 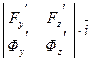- + уравнение нормальной плоскости: ·(х – х ₀) - ·(у – у ₀) + ·(z - z ₀) = 0.

Задача. Составить уравнение нормальной плоскости для кривой γ: в точке М для которой t = -1.

Решение. Найдем координаты точки М и вектор касательной.

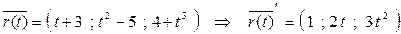
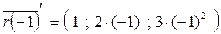= (1; -2; 3).

Тогда нормальная плоскость имеет уравнение:

1·(х – 2) + (-2)·(у – (-4)) + 3·(z – 3) = 0 х – 2 у + 3 z – 19 = 0.

Задача. Составить уравнение нормальной плоскости к кривой γ: в точке М (2; -1; 3).

Решение. Кривая γ заданная пересечением поверхностей: круговой цилиндр и гиперболический параболоид. Проверим принадлежность точки М поверхностям:

2² + (-1)² = 5 3 = 2² - (-1)²

Найдем вектор касательной:

F (х, у, z) =

F_х' = 2 х, F_y' = 2 у, F_z' = 0,

тогда производные в точке М(2; -1; 3) будут

F_х' = 2·2 = 4, F_y' = 2·(-1)= -2, F_z' = 0,

Ф (х, у, z) =

Φ_х' =2 х, Φ_y' = - 2 у, Φ_z' = -1.

Φ_х' = 2·2 = 4, Φ_y' = - 2·(-1)= 2, Φ_z' = -1.

= || (1; 2; 8)

Тогда нормальная плоскость имеет уравнение:

1·(х – 2) + 2·(у – (-1)) + 8·(z – 3) = 0 х + 2 у + 8 z – 24 = 0.

Не нашли, что искали? Воспользуйтесь поиском: