
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Соприкасающаяся плоскость
Пусть дана некоторая кривая γ и точка М 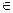 γ. Рассмотрим окрестность точки М. Пусть π - некоторая плоскость, проходящая через точку М и К
γ. Рассмотрим окрестность точки М. Пусть π - некоторая плоскость, проходящая через точку М и К 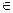 γ.
γ.
Обозначим КМ= d, ρ (π, К)= h 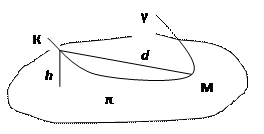
Определение. Если 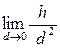 = 0, тогда плоскость π называется соприкасающейся плоскостью для кривой γ в точке М.
= 0, тогда плоскость π называется соприкасающейся плоскостью для кривой γ в точке М.
Теорема. Любая регулярная кривая в любой своей точке имеет соприкасающуюся плоскость. Причем эта плоскость или единственна или любая плоскость содержащая касательную является соприкасающейся.
Доказательство. Предположим, что такая плоскость есть и 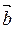 - единичный вектор нормали для этой плоскости.
- единичный вектор нормали для этой плоскости.
Тогда h = 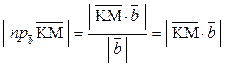 .
.
Т.к. 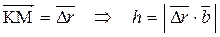 и
и 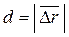
Разложим вектор-функцию в ряд Тейлора:
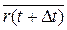 =
=  +
+ 
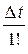 +
+ 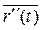
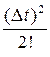 +
+ 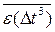

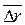 =
= 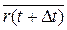 -
-  =
=  Δ t +
Δ t + 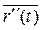
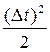 +
+ 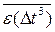

h = 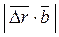 =│(
=│( ·
· 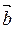 ) Δt+ (
) Δt+ (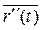 ·
· 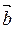 )
) 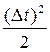 +
+ 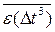 ·
· 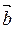 │
│
Т.к. 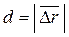
 d 2 =
d 2 = 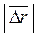 2 =│
2 =│  Δ t +
Δ t + 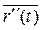
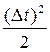 +
+ 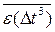 │2 =
│2 =  2Δ t 2+ ε1(Δ t 3)
2Δ t 2+ ε1(Δ t 3)
Т.о., если плоскость соприкасающаяся тогда 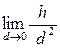 = 0
= 0 
0= 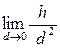

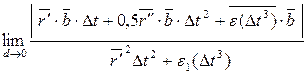
Если  ·
· 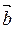 ≠0, тогда
≠0, тогда 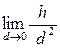 =∞,
=∞,
Если  ·
· 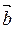 =0 и
=0 и 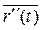 ·
· 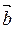 ≠0, тогда
≠0, тогда 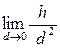 =
= 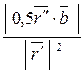 ≠0,
≠0,
Если  ·
· 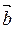 =0 и
=0 и 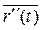 ·
· 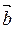 = 0, тогда
= 0, тогда 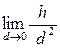 = 0.
= 0.
Т.о.  ·
· 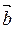 =0 и
=0 и 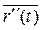 ·
· 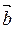 = 0
= 0 
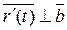 и
и 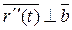
Если векторы  и
и 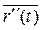 не коллинеарны и отличны от нулевого вектора, тогда единичный вектор нормали соприкасающейся плоскости определяется однозначно
не коллинеарны и отличны от нулевого вектора, тогда единичный вектор нормали соприкасающейся плоскости определяется однозначно 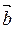 ║
║  ×
× 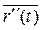 .
.
Если векторы  и
и 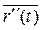 ·- коллинеарны или один из них равен нулевому вектору, то любая плоскость будет соприкасающейся.
·- коллинеарны или один из них равен нулевому вектору, то любая плоскость будет соприкасающейся.
Вывод: Нормальный вектор соприкасающейся плоскости 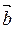 ║
║  ×
× 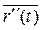 .
.
Замечание. Если кривая γ – плоская и лежит в плоскости α, то α и будет соприкасающейся плоскостью.
Обозначение: В дальнейшем единичный вектор, перпендикулярный соприкасающейся плоскости, будем обозначать 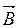
Задача. Составить уравнение соприкасающейся плоскости для кривой γ: 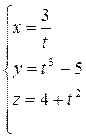 в точке М для которой t = -1.
в точке М для которой t = -1.
Решение. Найдем координаты точки М и векторы первой и второй производных.
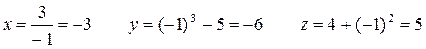
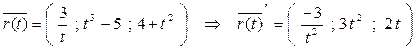
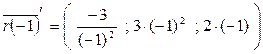 = (-3; 3; -2).
= (-3; 3; -2).
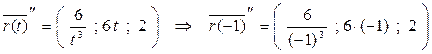 = (-6; -6; 2)
= (-6; -6; 2)
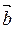 ║
║  ×
× 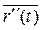 =
= 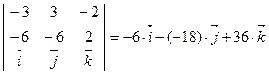 || (1; -3; -6)
|| (1; -3; -6)
Тогда соприкасающаяся плоскость имеет уравнение:
1·(х – (-3)) + (-3)·(у – (-6)) + (-6)·(z – 5) = 0  х – 3 у - 6 z – 15 = 0.
х – 3 у - 6 z – 15 = 0.
Не нашли, что искали? Воспользуйтесь поиском: