Жарықтың екі жақты қасиетінің бар екендігін кім айтты және ол неге сүйеніп дәлелдеді? 1 страница

Кванттық механика, толқындық механика – микробөлшектердің (элементар бөлшектердің, атомдардың, молекулалардың, атом ядроларының) және олардың жүйелерінің (мысалы, кристаллдардың) қозғалу заңдылықтарын анықтайтын, сондай-ақ, бөлшектер мен жүйелерді сипаттайтын физикалық шамаларды макроскопиялық тәжірибеде тікелей өлшенетін шамалармен байланыстыратын теория. Ол өрістің кванттық теориясында, кванттық химияда, кванттық статистикада, т.б. қолданылады. Кванттық механика бейрелятивистік (жарық жылдамдығымен салыстырғанда төмен жылдамдықтағы с) және релятивистік (жарық жылдамдығымен салыстыруға болатын жоғары жылдамдықтағы с) болып бөлінеді. Бейрелятивистік кванттық механика (өзінің қолданылу аймағындағы Ньютон механикасы сияқты) – толық аяқталған, қайшылықтары жоқ, өз саласында кез келген есептерді шешуге мүмкіндігі бар теория. Керісінше, релятивистік кванттық механиканы мұндай теория қатарына жатқызуға болмайды. Классикалық механика кванттық механиканың жуықталған дербес түрі болып саналады.

49. Анықталмағандық қатынастар

Анықталмағандық принципі — физикалық жүйені сипаттайтын (қосымша физ. шамалар деп аталатын) шамалардың (мыс., координат және импульс) бір мезгілде дәл мәндер қабылдай алмайтындығын тұжырымдайтын кванттық теорияның іргелі қағидасы. 1927 ж. неміс физигі Вагнер Гейзенберг ашқан. Анықталмағандық принципі материя бөлшектерінің (электрондар, протондар, т.б.) корпускулалық-толқындық табиғаты болатындығын айқындайды. Сандық тұрғыдан Анықталмағандық принципі былай тұжырымдалады: егер — жүйенің инерция центріндегі координатының анықталмағандық мәні, ал импульсының осіне проекциясының анықталмағандық мәні болса, онда осы анықталмағандықтардың көбейтіндісі Планк тұрақтысынан () кем болмайды Макроскопиялық шамалармен салыстырғанда аз шама болғандықтан, бұл қатынас атомдық масштабтағы құбылыстарға қатысты ғана орындалады. Анықталмағандық принципі атом ішіндегі құбылыстардың заңдылықтарын түсіндіру және кванттық механика саласының қалыптасуы кезінде аса маңызды рөль атқарды. Егер 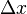және 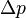сәйкесінше координаттың және импульстың орташа квадраттық ауытқулары болса:

,

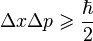мұндағы 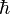— келтірілген Планк тұрақтысы. Анықталмағандық қатынасы - екі орайлас физикалык шамалар мәніндегі анықталмағандықтардың көбейтіндісі (мысалы, импульс пен координатаның, энергия мен уақыттың) Планк тұрақтысынан кіші болуы мүмкін емес дейтін тұжырым.^[1] Қозғалып келе жатқан, импульсі р бөлшекпен байланысқан де Бройль толқынының интенсивтігі бөлшектікеңістіктің берілген аумағынан табу ықтималдығын анықтайтыны өткен тақырыпта айтылды. Жазық монохромат толқын х осінің бойымен таралып жатсын. Онда бұл толқынға сәйкес бөлшектің импульсі р = р_х бірмәнді дәл анықталған. Бірақ жазық монохромат толқынның амплитудасы барлық жерде бірдей, сондықтан біз бөлшектің қай жерде екенін біле алмаймыз, яғни оныңкоординатасы анықталмаған. Бұл қиындықтан шығу үшін бөлшекті монохромат толқынмен емес, жиіліктері бір-біріне өте жақын бірнеше толқындардың қосындысымен, яғни ұзындығы Δх болатын толқындық пакет арқылы модельдеп көрейік. Толқындық пакеттің амплитудасы бөлшек орналасқан кеңістіктің кішкене аумағынан басқа жердің бәрінде нөлге тең, ал бөлшектің жылдамдығытолқындық пакеттің топтық жылдамдығына тең болсын. Енді біз бөлшектің координатасын қандай да бір Δх дәлдікпен анықтай аламыз, бірақ толқын ұзындығын λ=Δх/n (мұндағы n — Δх ұзындыққа сыятын толық периодтардың саны) дәл анықтай алмаймыз. Себебі толқындық пакеттің шекарасы дәл тағайындалмайды. Олай болса, λ=h/p болғандықтан, импульстің мәні де Δр_x шамасына анықталмайды. n неғұрлым үлкен болса, толқын ұзындығын, ол арқылы импульсті соғұрлым дәл анықтаймыз. Бірақ n өскен сайын координатаны анықтау дәлдігі төмендей береді, себебі толқындық пакеттің ұзындығы артады. Біз бұл жерде сәйкес оське қатысты координата мен импульстің проекциясын бір мезетте анықтау туралы айтып отырмыз.

Бірінің мәнінің анықталмағандығы екіншісін өлшеу дәлдігіне тәуелді шамалар жұбын (мысалы, х пен р_x) түйіндес шамалар деп атайды.

Жарық деген не? Бұл сұраққа ғалымдар көне аманнан жауап іздеп келді. XIX ғасырға дейін жарық тез қозғалатын бөлшектер — корпускулалар ағыны ретінде қарастырылып келді. Бұл көзқарасты И. Ньютон да ұстанды. Бірақ, XIX ғасырда жарықтың толқындық қасиеттері айқын білінетін оның интерференциясы, дифракциясыжәне т.б. құбылыстар ашылды. Юнг пен Френель жұмыстарының нәтижесі екі бәсекелес корпускулалық және толқындық теорияның біреуі, яғни толқындық теорияның жеңіп шығуына әкелді. Бұдан соң Максвелл еңбектерінің қорытындысы жарықтың электромагниттік толқын екенін түпкілікті дәлелдеп берді.

Бірақ XIX ғасырдың аяғы мен XX ғасырдың басында ашылған құбылыстар (оларды біз осы тарауда қарастырып өттік) жарықтың фотондар ағыны ретінде таралатынын көрсетті. Сонымен, жарық деген не? Толқын ба әлде бөлшек пе деген сұрақ қайта туындады. Физик ғалымдар бірте-бірте сұрақты бұлай қоюдың өзі дұрыс емес екенін түсінді.

Жарықта әрі үздіксіз электромагниттік толкындардың, әрі дискретті фотондардың бөлшектік қасиеттері бар. Абсолют қара дененің сәулеленуін және жарық қысымыныңфлуктуацияларын зерттей отырып, жарық қасиеттерінің екіжақтылығын алғаш түсінген Эйнштейн болды. Ол осы айтылған ауытқуларды есептейтін формуланы қорытып шығарды. Бұл формула екі қосылғыштан тұрады, бірінші қосылғыш — "кванттық мүше" жарықты фотондардың ағыны ретінде сипаттаса, екінші қосылғыш — "толкындық мүше" таралатын электромагниттік толқындағы флуктуацияларды сипаттайды. Жиілік жоғары болса, "кванттық мүшенің", төменгі жиіліктерде "толқындық мүшенің" үлесі басым болады. Белгілі оптикалық құбылыстардың заңдылықтарын зерделей отырып, толқын ұзындығы азайған сайын (немесе, жиілік артқан сайын) жарықтың кванттық қасиеттері айқын біліне бастайтынына (және керісінше) көз жеткізуге болады.

Егер жарықтың таралу процесіне статистикалық тәсіл тұрғысынан қарасақ, оның толқынды қорпускулалық екіжақтылық қасиеттері түсінікті бола бастайды. Кванттық көзқарас бойынша жарық — энергия мен импульс және массаға ие фотондардың ағыны. Жарық қандай да бір оптикалық жүйе арқылы (мысалы, дифракциялық тордан) өткенде, фотондар онымен әсерлесіп, кеңістікте қайта орын алмастырып, орналасады. Соның нәтижесінде, мысалы, дифракциялың көрініс бақыланады. Экранның берілген нүктесінің Е жарықталынуы уақыт бірлігінде осы нүктеге түскен барлық фотондар энергияларының қосындысына, олай болса n₀ фотондар санына пропорционал. Сонымен, Е және n₀ шамалары экранның берілген нүктесіне фотондардың түсу ықтималдылығына пропорционал. Толқындық көзқарас бойынша J жарықталыну интенсивтікке, ал оның өзі амплитуданың квадратына пропорционал, яғни Е ~ А². Осы екі көзқарасты салыстыра отырып, мынадай қорытындыға келеміз: кеңістіктің қандай да бір нүктесіндегі жарық толқыны амплитудасының квадраты осы нүктеге фотондардың келіп түсу ықтималдылығын анықтайды.

Сонымен, жарықтың корпускулалық және толқындық қасиеттері бірін-бірі жоққа шығармайды, керісінше олар бір-бірін толықтырады. Сәулеленудің корпускулалық касиеттері оның энергиясы, импульсі және массасы үзікті бөлшектер — фотондарда жинақталуымен байланысты болса, толқындық қасиеттері осы фотондардың кеңістікте орналасуының статистикалық заңдылықтарымен байланысты. Тәжірибелер толқындық қасиет тек фотондардың ағынына ғана емес, жеке фотонға да тәнекенін көрсетті. Фотон дифракциялық тордан өткен соң экранның қай нүктесіне келіп түсетінін дәл анықтап айту мүмкін емес, тек әр фотонның экранның қандай да бір нүктесіне түсу ықтималдығын ғана есептеуге болады. Осы тақырыпта айтылғандардан фотондар Ньютонның корпускулаларынан мүлде өзгеше бөлшектер екенін көреміз. Ньютон корпускулалары кәдімгі классикалық бөлшектердің қасиетіне ие болса, фотондар әрі бөлшек, әрі толқындық қасиетке ие.

Жарықтың кванттық қасиеттерін сипаттайтын құбылыстарға қандай құбылыстар жатады? Жарық энергиясын электр энергиясына айналдыру арқылы не ұтамыз?

Кванттық механика, толқындық механика – микробөлшектердің (элементар бөлшектердің, атомдардың, молекулалардың, атом ядроларының) және олардың жүйелерінің (мысалы, кристаллдардың) қозғалу заңдылықтарын анықтайтын, сондай-ақ, бөлшектер мен жүйелерді сипаттайтын физикалық шамаларды макроскопиялық тәжірибеде тікелей өлшенетін шамалармен байланыстыратын теория.

Ол өрістің кванттық теориясында, кванттық химияда, кванттық статистикада, т.б. қолданылады. Кванттық механика бейрелятивистік (жарық жылдамдығымен салыстырғанда төмен жылдамдықтағы с) және релятивистік (жарық жылдамдығымен салыстыруға болатын жоғары жылдамдықтағы с) болып бөлінеді.

Бейрелятивистік кванттық механика (өзінің қолданылу аймағындағы Ньютон механикасы сияқты) – толық аяқталған, қайшылықтары жоқ, өз саласында кез келген есептерді шешуге мүмкіндігі бар теория. Керісінше, релятивистік кванттық механиканы мұндай теория қатарына жатқызуға болмайды. Классикалық механика кванттық механиканың жуықталған дербес түрі болып саналады.

Тарихы[өңдеу]

20 ғасырдың бас кезінде классикалық физикада түсінік таппаған бірнеше құбылыстар (қызған дененің сәуле шығаруы, фотоэффект, Резерфорд атомының орнықтылығы, т. б.) тәжірибе жүзінде ашылды. Тәжірибеде қызған денеден шыққан сәуле қарқындылығының (интенсивтігінің) максимумы әр уақытта белгілі бір толқын ұзындығына сәйкес келетіндігі және ол максимум температура жоғарылаған сайын [[қысқа толқындар[[ жағына ығысатындығы байқалады. Мысалы, қызған темірдің түсі күрең қызылдан бастап, температура жоғарылаған сайын ашық түске боялып, соңынан ағарып кетеді. Демек температура жоғарылаған сайын қысқа толқынды жарық сәулесінің спектрдегі үлесі артады. Классиклық физика жылулық сәуле шығарудың спектрінде байқалатын заңдылықты мүлдем түсіндіре алмады. Оған себеп классиклық физика бойынша қызған дене әр уақытта қысқа толқынды сәуле шығаруға тиіс. Сонымен қатар классиклық физика тұрғысынан түсінік таппаған тағы бір құбылыс – фотоэффект құбылысы. Бұл құбылыс кезінде зат бетіне түскен сәуле, одан электрондар бөліп шығарады; ұшып шыққан электрондардың энергиясы зат бетінде жұтылған сәуленің қарқындылығына байланысты болмай, оның жиілігіне тәуелді болуы түсініксіз болды. Егер түскен сәуленің жиілігі белгілі бір шамадан кем болса, онда жарықтың қарқындылығы қаншалықты артқанымен, электрондар заттан сыртқа қарай ұшып шыға алмайды. Ал классиклық физика тұрғысынан электрондардың энергиясы жарықтың қарқындылығына, яғни затқа түскен сәуле толқынының энергиясына байланысты болуы керек. Жылулық сәуле шығару және фотоэффект құбылыстарын түсіндіру нәтижесінде жаңа теорияның, яғни кванттық механиканың негізі қаланды. Кванттық ұғымдарды (қараңыз Квант) алғаш рет 1900 жылы М. Планк қызған денелердің жылулық сәуле шығаруын толық түсіндіретін еңбектерінде (теориясында) жариялады. Бұл теория бойынша жарық үздіксіз түрде емес (классикалық теория бойынша) белгілі бір үлеспен үздікті (дискретті (1) өрнегімен анықтады, мұндағыn) кванттар түрінде шығарылады немесе жұтылады. Бұл кванттың энергиясын Планк: =h 10-34 Джс×h=6,62 – Планк тұрақтысы –n, шығарылатын (жұтылатын) жарықтың жиілігі. Планктың осы еңбегін ескере отырып 1905 жылы Альберт Эйнштейн фотоэффект теориясын ашты. Бұл теориясында Эйнштейн Планк идеясын дамыта отырып, мынадай болжам ұсынды: жарық тек үздікті түрде шығарылып (жұтылып) қана қоймай, ол кеңістікте үздікті кванттар ағыны түрінде тарайды. Үздіктілік (дискреттік) – жарықтың өзіне тән қасиет. Кейіннен кванттар фотондар деп аталды. Жарық фотоны басқа бөлшектермен тұтас бөлшек ретінде әсерлеседі, яғни жарыққа корпускулалық қасиет те тән. Жарықтың корпускулалық қасиетінің екінші бір қырын 1922 жылы америкалық физик А. Комптон (1892–1962) жарықтың бос электрондарда шашырау құбылысында (қараңыз Комптон эффектісі), фотон мен электронның серпімді соқтығысуын зерттейтін тәжірибеде байқады. Мұндай соқтығысудың кинематикасы мен динамикасы энергия мен импульстің энергиясынан басқаnсақталу заңдарымен анықталады. Осыдан барып фотонның =h /cn=hlp=h/ –lимпульсінің болуы керектігі туындайды (толқын ұзындығы, с – жарық жылдамдығы). Фотонның энергиясы мен импульсі = c×p өрнегімен байланысқан. Сонымен қатар интерференция, дифракция, поляризация құбылыстарын зерттеу кезінде жарықтың толқындық қасиеті де анық байқалған. Жарықтың екі жақтылық қасиетін = nh – толқынға тән шамалар. Бұдан логикалық қайшылық туындайды: бір құбылысты түсіну үшін жарық –nөрнегінен байқауға болады. Бұл өрнекте – бөлшекке, ал бөлшек, ал екіншісін түсіну үшін жарық – толқын ретінде қарастырылуы тиіс. Жарықтың осы қасиетінің микробөлшектерге де тән екендігі жөнінде 1924 жылы француз физигі Луй де Бройль (1892–1987) толқындық қасиет – тек жарық фотондарына ғана емес, материяны құрайтын барлық бөлшектерге (электрондар, протондар, мезондар, т.б.) тән қасиет деген болжам айтты (қараңыз Де Бройль толқындары).

Микробөлшектердің толқындық қасиеттері туннельдік эффект кезінде айқын байқалады. Бұл эффектіні түсіндіру арқылы классикалық физикада түсінік таппаған көптеген құбылыстардың (автоэлектрондық эмиссия, -ыдырауыaатом ядросының, т.б.) сыры ашылды.Осы қайшылықтарды шешу кванттық механиканың физикалық негіздерін жасауға мүмкіндік берді. Микродүниенің басқа да құбылыстарын зерттеу кезінде, әсіресе, атом құрылысын зерттеу кезінде, атом ішіндегі электрон қозғалысының классикалық физика заңдарына бағынбайтындығы және олардың энергияларының мүмкін болатын мәндері үздіксіз өзгермей, тек энергия деңгейлерінің дискретті қатарын құрайтындығы анықталды. Оң зарядты нүктелік ядро туғызатын өрісте қозғалатын электронға классикалық механиканың теңдеулерін қолдануға болмайды, яғни механика мен электрдинамика заңдарына негізделген Э. Резерфорд пен Н. Бор жасаған атом моделі орнықсыз болуға тиіс. Бірақ тәжірибе жүзінде атомның орнықты жүйе екендігі дәлелденді. Атомдарда стационар күйлер мен энергия деңгейлерінің бар екендігі Франк-Герц тәжірибесінде (1913–14) дәлелденді. Тәжірибеде байқалған атомдық құбылыстарды үйлестіру мақсатында Бор 1913 жылы екі қағида (постулат) (қараңыз Бор қағидалары) және оларға қосымша сәйкестік принципін ұсынды. Бұл принцип бойынша шектік жағдайда (кванттық сандардың үлкен мәндерінде) теориялық жолмен алынған формулалар классикалық физиканың заңдарына айналады. Бор квант тұрақтысы h -ты пайдалана отырып, заңдары классикалық механика заңдарынан өзгеше, сутек және сутек типтес атомдағы электрондардың қозғалысын анықтады. Сонымен қатар Бор теориясының жетістіктерімен бірге кемшіліктері де байқалды. Бұл теория электрондардың күрделі атомдардағы қозғалысын, атомдардың бір-бірімен байланысып молекулалар түзетіндігін, т.б. түсіндіре алмады. Атом теориясының одан әрі дамуына классикалық теорияның ұғымдары (траектория, орбита, т.б.) кедергі болды. Сондықтан электрондардың атомдағы қозғалысын толық сипаттау үшін атомның алғашқы және кейінгі стационар күйлеріне тәуелді шамалар ғана енетін жаңа теория жасау қажет болды. Осындай теорияны 1925 жылы неміс физигі В. Гейзенберг электронның координаттары мен жылдамдығының орнына абстрактылыалгебралық шамалар – матрицалар ғана енетін матрицалық механика жасау арқылы жүзеге асырды. Гейзенбергтің бұл жұмысын М. Борн мен П. Иордан одан әрі қарай дамытты. М. Борн 1926 жылы де Бройль толқынын ықтималдық теория тұрғысынан түсіндіру арқылы Гейзенбергтің матрицалық механикасы мен Э. Шредингердің толқындық механикасының эквиваленті екендігін дәлелдеді. Шредингер теңдеуі салыстырмалық теориясының талабын қанағаттандырмайды, ол жарық жылдамдығынан әлдеқайда төмен жылдамдықпен қозғалатын жүйенің күйін сипаттайды. Релятивистік тұрғыдан жалпыланған теңдеуді (қ. Дирак теңдеуі) 1928 жылы П. Дирак ұсынды. Дирак теңдеуі электронның спинінің (меншікті импульс моменті) болу себебін түсіндірді. Сонымен қатар Дирак теңдеуінен, массасы электронның массасына тең, оң бөлшектердің болатындығы анықталды. Электронның антибөлшегі “позитрон” деп аталды. Кейінірек табиғаттағы бөлшектердің көбінің антибөлшектері болатындығы айқындалды. Микробөлшектер классикалық статистикадан өзгеше кванттық статистикаға бағынады. Кванттық бөлшектердің статистикасы Ферми–Дирак статистикасы және Бозе–Эйнштейн статистикасы -мезондар, т.б. – “mболып екіге ажыратылады. Спиндері жартылай бүтін бөлшектер (электрондар, протондар, нейтрондар, фермиондар”) Ферми–Дирак статистикасының заңдарына бағынады. Кванттық статистиканың басты ерекшелігі – фермиондардың Паули принципіне -мезондар, т.б. –pбағынатындығы. Бұл принцип бойынша кванттық сандары бірдей екі фермион бір мезетте, бір күйде бола алмайды. Спиндері бүтін санға тең бөлшектер (фотондар, “бозондар”) Бозе–Эйнштейн статистикасына бағынады. Бозондар Паули принципіне бағынбайды, яғни кез келген күйде бір мезгілде қанша бөлшек болса да орналаса береді. Көп электронды күрделі атомдар үшін, кванттық механика есептерінің күрделілігі сонша, Шредингер теңдеуінің аналитикалық дәл шешімі табылмайды. Әр түрлі тәсілдердің көмегімен оның тек жуық шешімдері ғана алынады. Атомның энергия деңгейлері әр түрлі физикалық шамалармен сипатталатын төрт кванттық сандармен (қараңыз Кванттық сандар) анықталады. Электрондар Паули принципін сақтай отырып, әр энергия деңгейінде тек бір-бірден ғана орналасады. Атомның электрондық қабығының осылайша түзілуі химиялық элементтердің периодтық жүйесіндегі орналасу тәртібін түсіндіруге мүмкіндік береді. Кванттық механика – табиғаттың бұл заңдылығын алғаш түсіндірген бірден бір теория. Жылулық сәуле Бозе – Эйнштейн статистикасына бағынатын фотондардан тұратын жүйе ретінде қарастырылады. Мұндай тәсілді пайдаланып жылулық сәуленің спектрі бойынша энергияның таралу (үлестірілу) заңын анықтауға болады. Кванттық механика заңдары классикалық механиканың заңдарынан өзгеше болғанымен классикалық физиканың заңдарын жоққа шығармайды, оларды толықтырады. Кванттық механиканың кеңінен қолданыс тапқан бір саласы – соқтығысу теориясы. Әр түрлі соқтығысу және шашырау құбылыстарын зерттеуге кванттық механиканы пайдаланып, бөлшектердің бір-бірімен әсерлесу кезіндегі эффективтік қимасын есептеп шығаруға болады. Кванттық механика атомдармен қатар молекулалардың қасиетіндегі ерекшеліктерді, валенттілік теориясы мен химиялық күштердің табиғатын, қатты денелермен сұйықтықтардың көптеген қасиеттерін: асқын өткізгіштік пен ферромагнетизмді және асқын аққыштықты, т.б. толығымен түсіндірді. Кванттық механиканы релятивистік тұрғыдан жалпылау нәтижесінде сәуле шығарудың және әлі де болса қалыптасып бітпеген өрістің кванттық теориясы пайда болды. Кванттық механика физиканың көптеген саласында кеңінен пайдаланылып, елеулі нәтижелер беруде. Ол ядролық энергетиканың, радиоэлектрониканың, т.б-дың негізі болып саналады. Қазіргі кезде кванттық механика – физикалық негіздері түсінікті, математикалық аппараты жетілген, іргелі физикалық проблемаларды толық шешуге мүмкіндігі бар, дәйекті де жүйелі теория қатарына жатады.

Жел энергетикасы — жел энергиясын механикалық, жылу немесе электр энергиясына түрлендірудің теориялық негіздерін, әдістері мен техникалық құралдарын жасаумен айналысатын жаңартылатын энергетиканың саласы. Ол жел энергиясын халық шаруашылығына ұтымды пайдалану мүмкіндіктерін қарастырады. Елімізде арзан электр энергия көздерін іздеу мақсатында, “Қазақстанда 2030 жылға дейін электр энергиясын өндіруді дамыту туралы” мемлекеттік бағдарламаға сәйкес, жел күшімен өндіретін электр энергиясы қуатын халық шаруашылығына қолданудың тиімді жолдары қарастырылуда. Қазақстанда жел күшімен алынатын электр энергиясы қуатын кеңінен және мол өндіруге болады.

Жел энергиясының басқа энергия көздерінен экологилық және экономикалық артықшылықтары көп. Жел энергетикасы қондырғыларының технологиясын жетілдіру арқылы оның тиімділігін арттыруға болады. Жел энергиясын тұрақты пайдалану үшін жел энергетикасы қондырғыларын басқа энергия көздерімен кешенді түрде ұштастыру қажет. Республиканың шығыс, оңтүстік-шығыс, оңтүстік аймақтарында су электр станциялары мен жел электр станцияларын біріктіріп электр энергиясын өндіру өте тиімді. Қыс айларында жел күші көбейсе, жаз айларында азаяды, ал су керісінше, қыс айларында азайса, жаз айларында көбейеді. Сөйтіп, энергия өндіруді біршама тұрақтандыруға болады. Алматы облысының Қытаймен шекаралас аймағындағы 40-ендікте Еуразия мегабассейніндегі орасан зор ауа массасының көлемі ауысатын Орталық Азиядағы “жел полюсі” деп аталатын Жетісу қақпасындағы желдің қуаты мол. Ол екі таудың ең тар жеріндегі (ені 10 — 12 км, ұзындығы 80 км) табиғи “аэродинамикалық құбыр” болып табылады. Қақпа Қазақстанның Балқаш — Алакөл ойпатын Қытайдың Ебінұр ойпатымен жалғастырады. Осы жердегі жел ерекшеліктерін зерттеу нәтижесінде оның электр энергиясын өндіруге өте тиімді екені анықталды. Қыс кезінде желдің соғатын бағыты оңтүстік, оңтүстік-шығыстан болса, жаз айларында солтүстік, солтүстік-батыстан соғады. Желдің орташа жылдамдығы 6,8 — 7,8 м/с, ал жел электр станциялары 4 — 5 м/с-тан бастап энергия бере бастайды. Желдің қарама-қарсы бағытқа өзгеруі сирек болуына байланысты мұнда турбиналы ротор типті жел қондырғысын орнату тиімді. Желдің жалпы қуаты 5000 МВт-тан астам деп болжануда. Бұл өте зор энергия көзі, әрі көмір мен мұнайды, газды үнемдеуге және, әсіресе, қоршаған ортаны ластанудан сақтап қалуға мүмкіндік береді.

Не нашли, что искали? Воспользуйтесь поиском: