Зілісcіздік теңдеуі

Айталық, ағын түтігі бойымен үзіліссіз сұйық ағып жатсын. Мұндағы ағыс сұйық массасының сақталу заңын қанағаттандырады. Олай болса, ағын түтігінің көлденең қимасы s арқылы ∆t бірлік уақытта өтетін сұйық массасы ∆m мынаған тең болады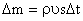

егер сұйық сығылмайды деп есептесек, онда s₁ қимадан ағып өтетін сұйық көлемі қандай болса, s₂ қимадан ағып өтетін сұйық көлемі де дәл сондай, сондықтан бұдан мұндағы екенін ескерсек онда , яғни, сығылмайтын тұтқыр емес сұйық ағысының жылдамдығы мен ағын түтігінің көлденең қимасының көбейтіндіcі берілген ағын түтігі үшін тұрақты шама болады. Бұл айтылған қорытынды ағынның үзіліссіздігі жөніндегі теоремасы деп аталады

Активтік, индууктивті, және сиымдылық кедергілері бар айнымалы ток тізбегі.Айнымалы ток деп ток күші, электр қозғаушы күші мен бағыты периодты түрде өзгеріп отыратын токты айтады. Тұрақты ток көзіне жалғанған конденсатордан ток жүрмейді. Ал, айнымалы ток көзіне жалғасақ, одан ток өтпейді. Әйтсе де конденсатор токтың жүруіне кедергі жасайды. Ол сиымдылық кедергі деп аталады

R_c= . айнымалы ток күші өткізгіштің формасына байланысты. Түзу өткізгіштің ток күші бірнеше орама бар өткізгішке қарағанда көп болатыны анықталған. Яғни орама көп катушкадан ток өткенде ток күші азаяды. Өткізгіштің осы кедергісін индуктивті кедергі деп атайды: R_L= . Тізбектей қосылған реостат, конденсатор мен катушканың толық кедергісі:

Z= мұндағы R- актив кедергі, (R_L-R_C)-реактивті кедергі, Z-импеданс. Тұрақты тоқ тізбек арқылы өткенде бөлінетін жылу мөлшері Джоуль –Ленц заңымен анықталады: Q=I²Rt

Инерция моменті — айналмалы қозғалыстағы қатты дененің инерттілігінің өлшемі Центрден тепкіш инерция моменті - механикалық жүйені құрайтын барлық нүктелердің массасын берілген тік бұрышты координаталар жүйесінің екі координатына көбейтіндісінің қосындыларына тең шама

Еркіндік дәрежесінің саны. Ішкі энергия. Еркіндік дәрежесінің саны – кеңістіктегі жүйенің күйін толық анықтайтын, тәуелсіз айнымалылардың саны. Реалды молекулаларда атом мен молекулалардың арасында тығыз байланыс жоқ, сондықтан молекулалардың ішіндегі атомдардың тербелмелі қозғалысының еркіндік дәрежесін де есепке алу керек. Молекулалардың жалпы еркіндік дәрежесінің санына байланыссыз, 3 еркіндік дәрежесі әрқашан жылжымалы. Олардың әрқайсысына молекулалардың жылжымалы қозғалысының кинетикалық энергиясын 1/3 береміз (e₀). 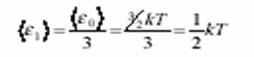Ішкі энергия U - бұл жүйедегі микробөлшектердің хаосты (жылулық) қозғалысының және осы бөлшектердің (молекула, атом, электрон, ядро т.с.с) әсерлесу энергиясы. Ішкі энергияға жүйедегі кинетикалық энергия және сыртқы потенциалдық энергия жатпайды.

Ішкі энергия - термодинамикалық жүйе күйінің бір мәнді функциясы, ал әр жүйе толығымен ішкі энергиясымен анықталынады. Сондықтан ішкі энергия жүйенің қазіргі күйге қалай келгеніне тәуелді емес. Ішкі энергияның өзгерісі бір күйден 2-ші күйге өткенде тек қана осы күйлердің ішкі энергиясының өзгерісімен анықталынады және ауысу жолына тәуелді емес.

Тұрақты электр тогы. Ом заңы Зарядталған бөлшектердің реттелген қозғалысын - электр тогы дейміз. Электр тогы ток күші деп аталатын шамамен сипатталады. Ток күші уақыт бірлігі ішінде берілген өткізгіштің көлденең қимасынан өтетін зарядтар шамасы: 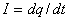. Бұл өрнек токтың лездік мәнін сипаттайды. Егер токтың күші мен бағыты уақыт өтуіне сәйкес өзгермейтін болса, онда мұндай ток тұрақты ток деп аталады: 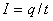; Мұндағы: q - өкізгіштің көлденең қимасы арқылы t уақыт ішінде өтетін электр заряды. Тоқ күшінің өлщемі - 1 Ампер. Электр тогы өзі өткен бет бойынша біркелкі таралмауы да мүмкін. Электр тогы сан жағынан ток тығыздығы деген шамамен сипатталады. Сонымен токтығыздығы деп өткізгіштің бірлік көлденең қимасынан өтетін ток күшін айтамыз: . Егер де ток өткізгіштің көлденең қимасынан біркелкі өтпесе, онда ток тығыздығы: .Егер dt уақыт ішінде өткізгіштің көлденең қимасы арқылы заряд тасымалданса 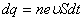(мұндағы n, e, 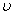- концентрация, заряд және зарядтың реттелген қозғалысының жылдамдығы), онда ток күші 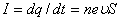Ал, өткізгіштегі ток тығыздығы мынаған тең болады: 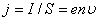. Тоқ тығыздығы - векторлық шама. Өлшем бірлігі: 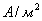Ом заңдары. Омның тағайындаған заңы бойынша біртекті металл өткізгіштің бойымен ағатын ток күші осы өткізгішке түсірілген U кернеуге пропорционал болады: . Бұл өрнек тізбек бөлігі үшін Ом заңы деп аталады. Тұйық тізбек үшін Ом заңы былай тұжырымдалады: тұйық тізбектегі ток күші э.қ.к.- і шамасына тура пропорционал да, тізбектің сыртқы және ішкі кедергілерінің қосындысына кері проорционал болады. Яғни, .Бөгде күштер әсер етейтін өткізгіш біртекті өткізгіш деп аталады. R шамасы өткізгіштің электрлік кедергісі деп аталады. Өлшем бірлігі: Ом. Өткізгіштің кедергісі өткізгіштің материалына, өлшеміне және формасына байланысты Біртекті цилиндр тәрізді өткізгіш үшін: . Мұндағы: l - өткізгіштің ұзындығы, S – оның көлденең қимасының ауданы, өткізгіштің меншікті электрлік кедергісі. Ом заңының дифференциалды түрі мынадай: 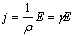. Мұндағы: - материалдың өткізгіштігі деп аталады.

Атом құрылысы. Резерфорд тәжірбесі. Бор постулаттары Атом ядролары абсолют шамасы жағынан электрон зарядына тең оң зарядталған протондар және электрлі бейтарап – нейтрондардан тұрады. Олар нуклон деп аталатын бөлшекті құрайды.Резерфорд тәжірибесі Атомның ішінде электр зарядтарының орналасу тәртібін анықтау үшін 1911 жылы Резерфорд өзінің шекірттері Г. Гейгер және Э. Марсденмен бірге альфа-бөлшектер шоғын өте жұқа алтын фольгадан өткізіп, бірнеше тәжірибелер жасады. Осы тәжірибелерді зерделеу нәтижесінде атомның ядролық, басқаша айтсақ, планетарлық моделі өмірге келді. Тәжірибеде алынған нәтижелерді зерделей отырып Резерфорд өз моделін ұсынды. Ол атомның оң заряды оның ортасында орналасқан радиусы шамамен 10^-15 м өте аз көлемге жинақталған деген қорытындыға келді. Бұл орталық бөлшекті Резерфорд ядро деп атады. Атомның массасы түгел дерлік ядрода шоғырланған. Ядроны айнала әр түрлі орбиталармен электрондар қозғалып жүреді. Ең шеткі электрон орбитасының радиусы атомның радиусына тең, R_a≈10^-10 м. Бұл үлгі Күн жүйесінің құрылымына ұқсайтын болғандықтан, оны атомның планетарлық моделі деп те атайды. Модель бойынша атом көлемінің басым көпшілік бөлігі "бос" болып шығады, ядроның радиусы атомның радиусынан 100 000 есе кіші. Орбиталардағы электрондардың теріс зарядтарының қосындысы ядроның оң зарядына тең, атом электрлік бейтарап. Бор постулаттары. Сызықтық спектрдің заңдылығын түсіндіру үшін Бор Резерфордтың

планетарлық атом моделі мен Планктың жарықтың кванттық табиғаты туралы гипотезаны біріктірді. Бор атомының теориясы 2 постулатпен негізделген: (I) Бордың бірінші постулаты (стационарлық жағдайдағы постулат): Атомдарда әнергия шығармайтын стационарлы (уақыт бойынша өзгермейтін) жағдайлар бар. Атомның стационарлы жағдайына стационарлық орбиталар бойымен қозғалатын әлектрондар сәйкес келеді. Әр стационарлық жағдай әнергияның шектелген (дискретті) шамасымен сипатталады. Стационарлы орбита бойындағы әлектрондардың қозғалысы әлектромагниттік толқынның сәуле шығаруымен анықталмайды. Бордың орбиталдық кванттық ережесі бойынша атомның стационарлық жағдайындағы әлектрон орбитаның бойымен қозғала отырып, төмендегі шартты қанағаттандырады

ипмульс моментінің кванттық мәніне ие болуға тиіс. Мұндағы -әлектронның массасы, - ші радиус орбитасындағы жылдамдығы . (II) Бордың екінші постулаты (жиілік ережесі): Атом бір стационарлық күйден екіншісіне көшкенде бір фотон 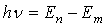стационарлық күйлерге сәйкес әнергиялар айырмасына тең әнергиямен шығарылады және жұтылады.

Сәуле шығару атомның көп әнергиялы жағдайынан аз әнергиялы жағдайына ауысуы кезінде болады (әлектронның ядродан көбірек алыстатылған орбитадан ядроға жақын орбитаға ауысуы).

Фотонның жұтылуы 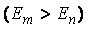атомның көп әнергиялы жағдаймен ауысуымен шығарылады (әлектронның ядродан көбірек алыстатылған орбитаға ауысуы).Кванттық өтулердің барлық мүмкін болатын дискретті жиілігінің жиыны: атомның сызықтық спектрін сипаттайды.

тогы бар өткізгіштердің әсерлесуі. ампер күші. сол қол ережесі. Ампер күші. Магниттік өрісте орналасқан ток ағатын өткізгішке әсер ететін F_А Ампер күші деп аталады.F_A = IB∆L F_A – Ампер күші, В-магнит өрісінің магнит индукциясы(Тл),I Ток күші (А),∆L- тогы бар өткізгіштің магнит өрісіндегі ұзындығы(м), -∆L ұзындығындағы I тогы бар өткізгіш бағытымен магнит индукциясы бағыты арасындағы бұрыш. Ампер күшнің бағыты сол қол ережесімен анықталады: сол қолымыздың алақанына кіретіндей етіп, тік төрт саусақтың бағытын ток бағытына көрсетеді. Барлық электр моторлар Ампер күшініің негізінде жұмыс істейді.

Еркін гармоникалық тербеліс Еркін тербелістер деп дене тепе-теңдік күйінен шығарылғаннан соң сыртқы күштің әрекетінсіз болатын тербелістерді айтады, Серіппеге бекітілген жүктің не жіпке ілінген жүктің тербелістері еркін тербелістерге мысал бола алады. Алдыңғы тақырыпта алынған тербеліс периодының формулалары осы еркін тербелістерге қатысты. Еркін тербелістердің жиілігін жүйенің меншікті тербеліс жиілігі немесе меншікті жиілік деп те атайды. Тербелістің меншікті жиілігі тербелмелі жүйенің қасиеттеріне, яғни серіппелі маятникте дененің массасы мен серіппенің қатаңдығына, ал математикалық маятникте оның ұзындығына байланысты анықталады.Сонымен, серіппелі және математикалық маятниктер еркін тербелістер жасайды. Мұндай тербелістер табиғатта кептеп кездеседі.

Маятниктердің тербелістерімен танысқаннан кейін, бізге енді дене қандай жағдайда еркін тербелістер жасайтынын ұғыну қиын емес. Біріншіден, тербелмелі жүйеде біріне-бірі "ұқсас" күштер әрекет етуі керек. Серіппелі маятникте бұл — серпімділік күші. Оның координаталар осіне түсірілген проекциясы (Ғ_х = -kx) серіппенің деформациясына, яғни дененің ығысуына пропорционал болады. Бұл күш тербелген дененің тепе-теңдік күйіне қарай бағытталған. Жіпті маятникте бұл — ауырлық күші мен серпімділік күшіне теңәрекетті күш.. Екіншіден, жүйедегі үйкеліс мейлінше аз болуы керек, олай болмаған жағдайда тербеліс тез өшіп қалады. Себебі үйкеліс күші қозғалысқа қарсы бағытталғандықтан, оның әрекетінен теріс жұмыс өндіріледі де, механикалық энергия азаяды. Энергияның азаюымен амплитуда кемиді. Сөйтіп, тербеліс өшеді. Өшетін тербелістерді гармоникалық тербелістер деп есептеуге болмайды, өйткені гармоникалық тербелістерде амплитуда тұрақты Гармоникалық тербеліс Гармоникалық тербелмелі қозғалыс деп нүкте қозғалысының тепе-теңдік қалпынан ауытқу шамасының синусоид н/се косинусоида бойымен периодты түрде қайталанып отыруын айтамыз. Егер тербелістегі нүктенің тепе-теңдік қалпынан ауытқу шамасын х арқылы белгілесек, онда осы ауытқудың уақытқа байланысты өзгеруі мына формуламен (28-сурет)өрнектеледі:

Ом заңы. Өткізгіштердің кедергісі. 1827 жылы неміс ғалымы Ом (1787-1854) көптеген тәжірбиелердің нәтижесінде мынадай қорытынды шығарды: тұрақты температурада (Т=const) өткізгіштің ұштарындағы кернеудің ток шамасына қатынасы әр уақытта тұрақты болады: U/I=R, мұндағы R шамасы өткізгіштің кедергісі деп аталады.Өткізгіштің кедергісі оның пішініне және мөлшеріне, сол сияқты табиғаы мен температурасына тәуелді. Осы формула арқылы кедергінің өлшем бірлігін тағайындауға болады. Кедергінің бірлігі үшін кернеуі 1В өткізгіштегі ток 1А болатын өткізгіштің кедергісі алынады. Оны Ом деп атайды. 1Ом = 1B/1A I=U/R Бұл Ом заңының формуласы болап табылады. Сонымен ток шамасы өткізгіштің ұштарындағы кернеуге тура пропорционал да, кедергісіне кері пропорционал екен. Өткізгіштің кедергісіне кері шама өткізгіштік деп аталады: QUOTE =f(U) Кедергінің кері шамасы,яғни өткізгіштік симеспен (См)өлшенеді. Әр түрлі өткізгіштер үшін ток пен кернеу арасында мынадай тәуелділік бар: I=f(U) Бұл байланыс өткізгіштің вольт-амперлік сипаттамасын көрсетеді. Сондықтан Ом заңы өткізгіштің ұштарындағы кернеу мен токтың сызықтық байланысын білдіреді. Мысалы,металдар мен электролиттер үшін Ом заңы кең түрде орындалады. Ом табиғаттары мен мөлшерлері әр түрлі көп теген өткізгіштерді зерттей отырып, біртекті цилиндр тәрізді басқа өткізгіштердің кедергісі оның ұзындығына тура пропорционал да, көлденең қимасына кері пропорционал болатындығын көрсетті:

мұндағы пропорционалдық коэффициент - өткізгіштің меншікті кедергісі, ол өткізгіштің қандай заттан жасалғанын көрсетеді. Меншікті кедергінің кері шамасы меншікті өткізгіштік деп аталады:

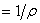 Мұның өлшем бірлігі сименс бөлінген метр (См/ м). Ал меншікті кедергінің өлшеміне алынады. Меншікті кедергі өте аз болатын материалға күміс ( және мыс - Cu (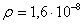), сондай-ақ алюминий- () жатады. Өткізгіштердің меншікті кедергісі зат құрамындағы қоспаларға байланысты. Өткізгіштерді тізбекке қосудың екі түрі бар: егер өткізгіштерді тізбектей қоссақ, онда олардың толық кедергісі

болады. Өткізгіштерді параллель қоссақ, онда олардың толық кедергісі

Поляри. жарықты медицинада қолдану Жарықтың полярлануы, жарық поляризациясы — жарық толқынының электр және магнит өрістері кернеуліктері векторларының (Е және Н) жарық сәулесі жазықтығынаперпендикуляр жазықтықта бағдарлануының реттелуі. Электр өрісі кернеулігі (Е) мен жарық сәулесі жататын жазықтық полярлану жазықтығы деп аталады. Жарықтың полярлынуы сызықтық жарықтың полярлынуы (Е өзінің тұрақты бағытын сақтайды), эллипстік Жарықтың полярлынуы (Е-нің ұшы жарық сәулесіне перпендикуляр жазықтықта эллипс сызады) жәнедөңгелек жарықтың полярлынуы (Е-нің ұшы шеңбер сызады) болып ажыратылады. Жарықтың полярлануын полярланған приборлар, поляроидтар, т.б. арқылы алуға болады. Жарықтың полярлануы зат құрылысының кейбір ерекшеліктерін түсіндіруге мүмкіндік береді. “ Жарықтың полярлануы ” ұғымын И.Ньютон енгізген (1704 — 06). Жарықтың поляризациясы-жарықтың көлденеңдігін дәлелдейтін құбылыс. Малюс Заңы — анализатордан өткен сызықты поляризацияланған жарық қарқындылығының cos α-ге пропорционал азаятындығын өрнектейтін заң; мұндағы α — жарық поляризациясы жазықтығы мен прибор (анализатор) арасындағы бұрыш. Бұл заңды 1810 жылы француз физигі Э.Л. Малюс (1775 — 1812) ашқан. Егер І0 және І — анализаторға түсетін және одан шығатын жарық қарқындылықтарын сипаттаса, онда Малюс Заңы бойынша: І=І0cos2α түрінде орындалады. Өзгеше (сызықты емес) поляризацияланған жарықты екі сызықты поляризацияланған құраушылардың қосындысы түрінде қарастыруға болады. Олардың әрқайсысы үшін Малюс Заңы орындалады. Барлық поляризациялық приборлардан өтетін жарық қарқындылығы Малюс Заңы бойынша есептеледі, ал Малюс Заңы ескермейтін, α-ға тәуелді болатын шағылу кезіндегі шығындар басқа тәсілмен қосымша анықталады. Жарық қарқындылығын өлшеуге арналған оптик. құрал — поляризациялық фотометрдің құрылысы Малюс Заңына негізделген.

Айнымалы қозғалыс Дененің жылдамдығы тұрақты болса, ондай қозғалыс ты бірқалыпты қозғалыс деп атайды. Ал дененің жылдамдығы өзгеріп отырса, ондай қозғалысты айнымалы қозғалыс дейді. Айнымалы қозғалыстың қарапайым түріне теңайнымалы қозғалыс жатады. Теңайнымалы қозғалыс деп дененің жылдамдығы кез келген бірдей уақыт аралықтарында бірдей шамага өзгеріп отыратын қозғалысты айтады.Теңайнымалы қозғалыстардың қарапайым түрлеріне теңүдемелі және теңбаяулайтын қозғалыстар жатады. Теңүдемелі қозғалыс кезінде жылдамдық бірқалыпты артады. Теңбаяулайтын козғалыстың жылдамдығы әрбір уақыт бірлігінде бірдей шамаға кеміп отырады.

Жылдамдықтың өзгеру шапшаңдығын сипаттау үшін удеу деп аталатын шама енгізіледі.

Үдеу — жылдамдықтың өзгеру шапшандығым сипаттайтын шама; ол жылдамдық өзгерісінің осы өзгеріс болган уақыт аралығына қатынасын береді.

Халыкаралық бірліктер жүйесінде (SI) үдеу 1 м/с² -пен өлшенеді. Үдеудің формуласынан жылдамдықты табуға болады: v — v₀ + at. Айналмалы қозғалыстың кинематикалық тұрғыда сипаттайтын шамалар бурыштық удеу мен бурыштык жылдамдык Бұрыштық үдеу — бұрыштық жылдамдықтың өзгеру шапшаңдығын сипаттайтын векторлық шама; - бұрыштық жылдамдық өзгерісінің осы өзгеріс өткен уақыт аралығына қатынасымен анықталатын бұрыштық жылдамдықтың өзгеруінің лездігі. векторына қарсы бағытта болады. Бұрыштық үдеудің бірліктердіңw векторымен бағыттас, ал кемімелі айналғанда wБұрыштық үдеу векторы (α) айналу осінің бойымен бағытталады және ол дене үдемелі айналғанда халықаралық жүйесіндегі бірлігі: рад/с2.

Бұрыштық жылдамдық

Уикипедия — ашық энциклопедиясынан алынған мәлімет

Бұрыштық жылдамдық — қатты дененің айналу шапшаңдығын сипаттайтын векторлық шама; дененің айналмалы қозғалысыныңкинематикалық мөлшері, модулі өте аз уақыт ішінде айналу бұрышының сол уақытқа қатынасымен, ал бағыты айналу осінің бойымен дененің айналуы сағат тілінің бағытына қарсы бағытта көрінетін бағытымен бағыттас вектор. Модулі айналу бұрышының модулінен уақыт бойынша алынған туындыға тең. Дененің tD— jD, мұндағы қозғалмайтын осьтің төңірегінде бірқалыпты айналуы кезіндегі бұрыштық жылдамдығының сан мәні: уақыт) дененің бұрылуы бақылаушыға сағат тілі жүрісіне қарсы бағытта болып көрінетіндей бағыттағы айналу осінің бойымен бағытталады. Бұрыштық жылдамдықтың бірліктердің халықаралық жүйесіндегі бірлігі: рад/с.w бұрылу бұрышының өсімшесі. Ал жалпы жағдайда ол мынаған тең: Бұрыштық жылдамдықтың векторы (jішіндегі

Не нашли, что искали? Воспользуйтесь поиском: