Интерференция световых волн. Принцип суперпозии волн.

В соответствии с определением, данным выше, мы будем говорить об интерференции волн, когда при их совместном действии не происходит суммирования интенсивностей. Условием интерференции волн одной и той же частоты является их когерентность, т.е. сохранение неизменной разности фаз за время, достаточное для наблюдения.

Одним из первых ученых, кто наблюдал явление интерференции, был Томас Юнг, который получил интерференционную картину в установке, показанной на рисунке ниже.

Свет, предварительно прошедший через светофильтр, проходя через отверстие S в экране А, падал на экран В, в котором были проделаны две тонкие щели и . Эти щели являлись когерентными источниками света и давали достаточно четкую картину интерференции на экране Здесь и – источники когерентного излучения, и – пути света от источников до точки наблюдения Р, d – расстояние между щелями, L – расстояние между экранами В и С. Свет, предварительно прошедший через светофильтр, проходя через отверстие S в экране А, падал на экран В, в котором были проделаны две тонкие щели и . Эти щели являлись когерентными источниками света и давали достаточно четкую картину интерференции на экране Здесь и – источники когерентного излучения, и – пути света от источников до точки наблюдения Р, d – расстояние между щелями, L – расстояние между экранами В и С.

,

где λ- длина волны. В точке Р (рис. 1), складываясь, колебания дадут

.

Таким образом, колебание в точке Р имеет амплитуду, равную , и интенсивность, пропорциональную .

Рисунок 1. Ход лучей в опыте Юнга

Различие интенсивности света в разных точках зависит только от различия разностей расстояний s₂ и s₁. Благодаря этой разности расстояний, или, как принято говорить, разности хода двух волн , колебания, вызванные этими волнами в точке их встречи, будут обладать разностью фаз δ даже в том случае, когда начальные фазы обеих волн были одинаковы. Разность фаз δ, возникшая вследствие разности хода волн, равна

, (4)

где .

Из (4) следует, что если в разности хода укладывается целое число длин волн, то в этой точке будет наблюдаться интерференционный максимум, то есть

, (5)

где – длина волны в вакууме, то разность фаз оказывается кратной .

Если в укладывается полуцелое число длин волн, то будет возникать интерференционный минимум, то есть:

, (6)

Если начальные фазы одинаковы, то интенсивность двух интерферирующих волн с одинаковыми амплитудами запишется в виде

(7)

Целым значениям m соответствует интенсивность, пропорциональная 4А². При полуцелом m интенсивность равна нулю.

Описанное распределение интенсивностей представляет собой интерференционную картину, соответствующую интерференции двух когерентных волн с начальной разностью фаз, равной нулю.

В случае некогерентных волн каждому значению δ будет соответствовать своя интерференционная картина, которая с течением времени будет сменяться другой. Если их смена происходит достаточно быстро, то мы не в состоянии наблюдать эти мгновенные интерференционные картины и воспринимаем некоторое среднее состояние, которое соответствует монотонному распределению интенсивности.

Волны могут интерферировать, если соблюдаются условия временной и пространственной когерентности.

Временная когерентность. Временная когерентность – это когерентность колебаний, совершающихся в одной и той же точке пространства, но в разные моменты времени. Максимальная разность хода, при которой еще возможна интерференция, называется длиной когерентности , где 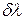– интервал длины волны колебания, обусловленный конечностью колебания.

Пространственная когерентность. Пространственная когерентность это когерентность колебаний совершающихся в один и тот же момент времени в разных точках пространства. В этом случае фаза колебания при переходе от одной точки волновой поверхности к другой изменяется беспорядочным образом. Введем расстояние , при смещении на которое вдоль волновой поверхности случайное изменение фазы достигает значения 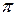. Колебания в двух точках волновой поверхности, отстоящих друг от друга на расстоянии меньше , будут приблизительно когерентными. Расстояние называется длиной пространственной когерентности или радиусом когерентности.

,

где – угол, под которым виден источник из данной точки.

Объем когерентности. Все пространство, занимаемое волной, можно разбить на части, в каждой из которых волна приблизительно сохраняет когерентность. Объем такой части пространства, называемый объемом когерентности, по порядку величины равен произведению длины временной когерентности на площадь круга радиуса : .

Необходимо заметить, что в создании получаемой интерференционной картины не участвует волна, отраженная от верхней (плоской) поверхности линзы, так как оптическая разность хода между этой волной и волнами, отраженными от границ воздушного зазора, больше длины когерентности для нелазерного света.

Суперпозиция волн

Принцип суперпозиции (наложения) волн заключается в следующем: в линейных средах волны распространяются независимо друг от друга, то есть волна не изменяет свойства среды, и другая волна распространяется так, будто первой волны нет. Это позволяет вычислять итоговую волну как сумму всех волн, распространяющихся в данной среде.

При сложении двух или более синусоидальных волн результирующая волна в общем случае уже не будет синусоидальной.

Рассмотрим в качестве примера результат сложения двух плоских однонаправленных волн с одинаковыми амплитудами и разными, но близкими частотами и волновыми числами:

Полученная волна не является синусоидальной, так как величина перед синусом (амплитуда волны) меняется со временем и координатой. Однако, если на длине волны (и в течении периода) её изменения малы (что имеет место при малых dk и dw), волна ещё похожа на синусоиду; её иногда называют квазисинусоидальной. График этой волны представляет собой то, что мы в теории колебаний назвали биениями; однако здесь, в отличие от маятника, биения происходят не только во времени, но и в пространстве.

Не нашли, что искали? Воспользуйтесь поиском: