ВЫЧЕРЧИВАНИЕ КОНТУРА ДЕТАЛИ С ПОСТРОЕНИЕМ СОПРЯЖЕНИЙ И ДЕЛЕНИЕМ ОКРУЖНОСТИ НА РАВНЫЕ ЧАСТИ

ЦЕЛЬ РАБОТЫ.

Научиться: 1) вычерчивать контур детали,

2) строить сопряжения,

3) делить окружность на равные части

4) наносить размеры.

КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Построение перпендикуляра к прямой из точки, лежащей вне прямой (рис. 1):

1. Из заданной точки С провести дугу окружности произвольного радиуса R, пересекающую прямую а в точках 1 и 2.

2. Из точек 1 и 2 провести дуги окружностей произвольного радиуса R1 до взаимного пересечения в точке D.

3. Через точки С и D провести прямую линию.

Линия CD перпендикулярна к заданной прямой а.

Рис. 1 Рис. 2

Деление отрезка пополам и построение перпендикуляра к середине отрезка (рис.2):

1. Из концов отрезка АВ проводят дуги радиусом R, величиной большей, чем половина отрезка.

2. Точки пересечения дуг соединяют прямой линией СD.

Линия CD является перпендикуляром к отрезку АВ, а точка О – середина отрезка.

Деление окружности на шесть равных частей (рис.3)

(Построение правильного шестиугольника, вписанного в окружность, например контура гайки или головки болта)

Сторона правильного шестиугольника, вписанного в окружность, равна радиусу окружности.

Для деления окружности на шесть равных частей надо из точек 1 и 4 пересечения центровой линии с окружностью сделать на окружности по две засечки радиусом R, равным радиусу окружности. Соединив полученные точки отрезками прямых, получим правильный шестиугольник.

Рис.3 Рис.4

2.3. Определение центра дуги окружности (рис.4)

1. Отметить на дуге две произвольные хорды АВ и ВС.

2. Построить перпендикуляры к серединам хорд.

3. Продлить перпендикуляры до их пересечения.

Точка О пересечения перпендикуляров является центром дуги.

Сопряжения

Сопряжением называется плавный переход от одной линии к другой.

Сопряжения осуществляют с помощью дуги окружности называемой окружностью (дугой) сопряжения.

Для построения сопряжения необходимо найти центр окружности сопряжения, при этом надо учитывать, что центр сопряжения всегда лежит на расстоянии радиуса сопряжения от заданной линии.

Внимание! Окружность сопряжения всегда строго касательна к заданным линиям. Если касание не получилось, ищите ошибку в построении.

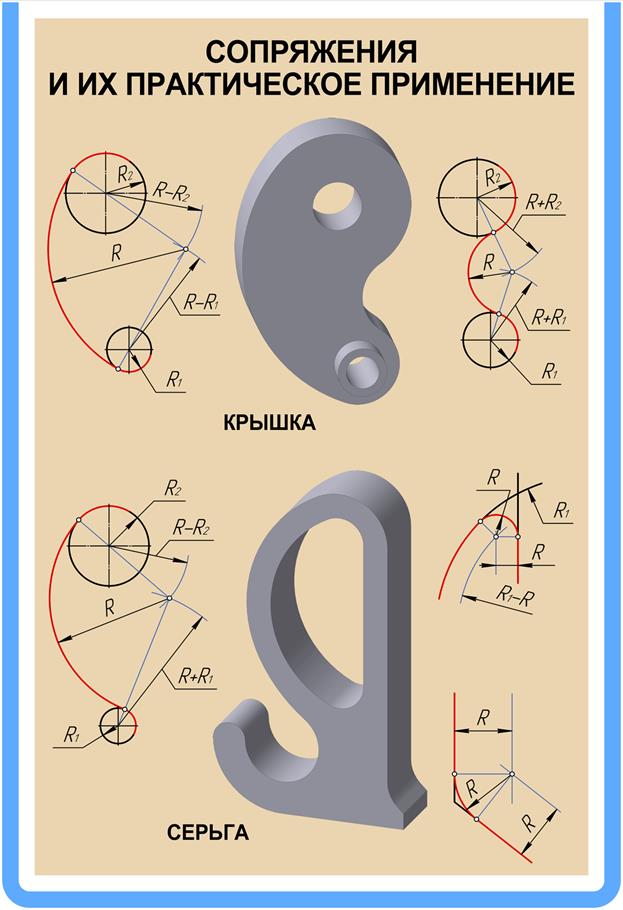
Рис.5

Сопряжение двух прямых линий при помощи дуги заданного радиуса. (рис.5 Серьга. Изображение снизу справа.)

Заданы две прямые (красные) и радиус сопряжения R.

1. Провести две вспомогательные прямые (синии), параллельные заданным, на расстоянии радиуса сопряжения R;

Точка пересечения вспомогательных прямых является центром дуги сопряжения.

2. Построить дугу сопряжения, т.е. из центра сопряжения радиусом R провести дугу сопряжения (красная).

Не нашли, что искали? Воспользуйтесь поиском: