Алгоритм построения кснф

1) Избавиться от всех логических операций, содержащихся в формуле, заменив их основными: конъюнкцией, дизъюнкцией, отрицанием. Это можно сделать, используя равносильные формулы:

2) Заменить знак отрицания, относящийся ко всему выражению, знаками отрицания, относящимися к отдельным переменным высказываниям на основании формул:

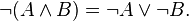
3) Избавиться от знаков двойного отрицания.

4) Применить, если нужно, к операциям конъюнкции и дизъюнкции свойства дистрибутивности и формулы поглощения.

6.Исчисление высказываний как формальная система. Доказательство теорем в исчислении высказываний. Разрешимость исчисления высказываний.

Основное понятие исчисления высказываний – высказывание. Это предложения на естественном языке, которые могут быть истинными или ложными. При этом различают логическую истину языка и фактическую истину.

7.Полные системы ФАЛ. Примеры. Критерий полноты

Система ФАЛ {f1, f2,…, fm} называется функционально полной, если с помощью функций, входящих в эту систему, применяя операции суперпозиции и подстановки, можно получить любую, сколь угодно сложную ФАЛ.

Различают 2 вида функциональной полноты:

Сильная функциональная полнота

Слабая функциональная полнота

В технических приложениях система функций {f1, f2,…, fm} называется функционально полной в слабом смысле, если функционально полной в сильном смысле является система {f1, f2,…, fm, 0, 1}.

9.Понятие логического элемента. Обозначения. Логическая схема.

Логические элементы (ЛЭ) – это электронные схемы, реализующие простейшие логические операции. ЛЭ теоретически может иметь любое конечное число входов, но на практике их количество обычно не превышает четырёх. Не все логические операции имеют соответствующие ЛЭ. На практике встречаются следующие ЛЭ: Задержка; НЕ; И; ИЛИ; И-НЕ; ИЛИ-НЕ; Чётность; Нечётность. Другие логические операции (например, импликация) не имеют соответствующих ЛЭ, и для их реализации приходится строить небольшие схемы из имеющихся ЛЭ

Логические элементы имеют один или несколько входов и один выход, через которые проходят электрические сигналы, обозначаемые условно 0, если "отсутствует" электрический сигнал, и 1, если "имеется" электрический сигнал. Простейшим логическим элементом является инвертор, выполняющий функцию отрицания. Если на вход поступает сигнал, соответствующий 1, то на выходе будет 0. И наоборот. У этого элемента один вход и один выход. На функциональных схемах он обозначается:

Логический элемент, выполняющий логическое сложение, называется дизъюнктор. Он имеет, как минимум, два входа. На функциональных схемах он обозначается:

Логический элемент, выполняющий логическое умножение, называется конъюнктор. Он имеет, как минимум, два входа. На функциональных схемах он обозначается:

Специальных логических элементов для импликации и эквивалентности нет, т.к. А => В можно заменить на А V В; А <=> В можно заменить на (A & B)V(A & B).

Другие логические элементы построены из этих трех простейших и выполняют более сложные логические преобразования информации. Сигнал, выработанный одним логическим элементом, можно подавать на вход другого элемента, это дает возможность образовывать цепочки из отдельных логических элементов. Например:

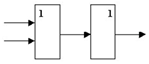
Эта схема соответствует сложной логической функции F(A,B)= (А V В).

Попробуйте проследить изменения электрического сигнала в этой схеме. Например, какое значение электрического сигнала (0 или 1) будет на выходе, если на входе: А=1 и В=0

10. Основные понятия в исчислении предикатов 1 порядка. Предикаты. Кванторы. Термы

В исчислении предикатов используются:

1. Предметные переменные x₁, x₂, …, x_n.

2. Предметные константы a, b, c, d, ….

3. Предикатные буквы A, B, C, D, ….

4. Функциональные буквы f, g, h, ….

5. Логические операторы Ø, É, Ù, Ú, Û.

6. Кванторы ", $.

Квантор — общее название для логических операций, ограничивающих область истинности какого-либо предиката. Чаще всего упоминают квантор всеобщности (обозначение: , читается: «для всех…», «для любого…» или «любой…») и квантор существования (обозначение: , читается: «существует…» или «найдется…»). Кванторы являются способом сокращенной записи конъюнктивных и дизъюнктивных формул. Так как область определения предикатов может быть бесконечной.

Не нашли, что искали? Воспользуйтесь поиском: