Системы счисления. Типы. Правила сложения и вычитания в различных системах счисления. Переводы из одной системы счисления в другие системы(2,8,10,16) счисления.

Перевод из 2СС в 10СС: умножаем каждый двоичный разряд справа налево на степень двойки, начиная с нулевой.

111001(2) = 1*2^5 + 1*2^4 + 1*2^3 +0*2^2 + 0*2^1 + 1*2^0 = 32 + 16 + 8 + 0 + 0 + 1 = 57(10)

Для перевода десятичного числа в 2(8,16) систему его необходимо последовательно делить на 2(8,16) до тех пор, пока не останется остаток, меньший или равный 1. Число в двоичной (8,16) системе записывается как последовательность последнего результата деления и остатков от деления в обратном порядке.

Чтобы перевести число из двоичной системы в восьмеричную, его нужно разбить на триады (тройки цифр), начиная с младшего разряда, в случае необходимости дополнив старшую триаду нулями, и каждую триаду заменить соответствующей восьмеричной цифрой.

Чтобы перевести число из двоичной системы в шестнадцатеричную, его нужно разбить на тетрады (четверки цифр), начиная с младшего разряда, в случае необходимости дополнив старшую тетраду нулями, и каждую тетраду заменить соответствующей восьмеричной цифрой

Для перевода восьмеричного числа в двоичное необходимо каждую цифру заменить эквивалентной ей двоичной триадой.

Для перевода шестнадцатеричного числа в двоичное необходимо каждую цифру заменить эквивалентной ей двоичной тетрадой.

При переходе из восьмеричной системы счисления в шестнадцатеричную и обратно, необходим промежуточный перевод чисел в двоичную систему.

Правила сложения в 2 сс:

0 + 0 = 0; 0 + 1 = 1; 1 + 0 = 1; 1 + 1 = 10;

24. Предваренные нормальные формулы. Алгоритм приведения к предваренной нормальной форме.
25. Элементарные автоматы. Этапы синтеза схемы конечного автомата.
26. Полином Жегалкина.

Полином Жегалкина — многочлен над кольцом Z_2, то есть полином с коэффициентами вида 0 и 1, где в качестве произведения берётся конъюнкция, а в качестве сложения — исключающее или (+ в кружочке).

Теорема Жегалкина — утверждение о существовании и единственности представления всякой булевой функции в виде полинома Жегалкина.

Полином Жегалкина представляет собой сумму по модулю два произведений неинвертированных переменных, а также (если необходимо) константы 1. Формально полином Жегалкина можно представить в виде:

Примеры полиномов Жегалкина:

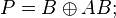
27. Равносильность формул исчисления высказываний. Нормальные формы: ДНФ и КНФ. Приведение к нормальной форме.

ДНФ строится:

1. Из таблицы истинности выписываются наборы переменных, где функция равна 0.

2. Наборы соединяются дизьюнкцией (+).

3. В наборах над переменной ставится отрицание, если в таблице истинности переменная равна 0.
4. Упрощение выражения.

КНФ строится:

1. Из таблицы истинности выписываются наборы входных переменных на которых функция равна0.

2. Наборы дизьюнкций(+) соединяются коньюнкцией(*).

3. В наборе над переменной ставится отрицание если она равна 1.

4. Упрощение выражения.

Не нашли, что искали? Воспользуйтесь поиском: