LL(1) - грамматикасы. 1 страница

5. Рекурсивтік түсу.

6. КС-грамматикасының бейнеленуі.

7. Сол жақ рекурсияның жойылуы. Сол жақ факторизация.

8. Енгізілген синтаксистік талдау. LL(1)-анализаторы.

9. Синтаксистік талдаудың құру және қолдану кестесі. LR талдауының ерекшелігі және нұсқасы.

1. Шығарылған синтаксистік талдау. LL(1) - грамматикасы.

Синтаксистік талдау – бұл оның, ол берілген мағынасына кейбір ерте берілген синтаксистік ережемен сәйкес келе ме? Мысалы, синтаксистік талдау мағынасы компиляторды жүзеге асырады. Егер рограмма синтаксистік тілге сәйкес келмесе, компилятор қатені көрсетеді.

Берілген бөлімде мысал ретінде талдау және арифметикалық есептеу мағынасын аламыз. Қарапайым мысалдан күрделі мысалға өте отырып, бір толыққанды калькулятор құраймыз. Берілген арифметикалық өрнекті операцияны санай алатын және м ауыспалы функцияны қолдана отырып, жақша арқылы жүзеге асырып өзгерте алатын.

Синтаксистік талдау – бұл процесс, онда лексем таблицасы орнатылады. Ол құрылымды шартты қамтамассыз етеді. Формуляцияланған және синтаксистік тілде анықалғаны анық.

Синтаксистік тілдің негізгі тапсырмасы – программа құрылымын талдау. Ереже сияқты құрылым ішінде ағаш түсіндіріледі, контексті еркін грамматикалық тілге сәйкес келетін. Қазіргі уақытта көбінесе LL(1)-талдау және LR(1)-талдау және оның варианты қлданылады. Рекурсивті жіберу көбінесе синтаксистік анализаторды қолмен программалағанда қолданылады, LR(1)-автоматты жүйе синтаксистік анализаторда қолдана отырып орындайды.

Синтаксистік талдаудың нәтижесі синтаксистік ағаш таблица объектісіне жіберу болып табылады. Синтаксистік талдаудың процесінде қателар табылады, программа құрылымымен байланысты.

Контекстік тілдің этаптары программа бөліктеріне тәуелділігі анықталады, контексті еркін синтаксистік жазылған.

Бұл негізхгі байланыс «суреттеу - қолдану», объектіге анализ типі, облысты талдау түрлері, параиетрлер сәйкестігі, белгілер және тағы басқа. Контексті талдау объект таблицасы нәтижесінде объектіні суреттеу ақпаратты толықтырады.

Ассемблер таблицасының құрылымы жоғарғы жылдамдығые іздеу қамтамассыз ету арқылы таңдалады. Команда таблицасы және директив әрқашанда мәлімет қоры болып табылады. Олар бір рет толтырылады – Ассемблерді өңдегенде, одан кейін өзгертілмеген болып қалады.

Бұл таблицалар тура хеширлеу функциясын құрады, мнемониканы таблицадағы адрес жазуы жүзеге асырады.

Тырысы мағынасын және функцияны хеширлеуді таңдауға ие. Таблицада коллизиялардың болмауы. Толтырылған таблицалар бір рет жүзеге асырылады, ал өту қайта-қайта шығару арқылы, бұл шығындар өтеледі.

Символ таблицасы динамикалы қалыптасады. 1-өткелдегі жұмыс нәтижесі. Сол таблицадағы іздеу 1-деңгей өткелде жүзеге асады.

Бұл таблицаның құрылымы тура өту таблицасы сияқты дұрыс емес. Сондай-ақ коллизиялардың дұрыс еместігі. Сондықтан символ таблицадағы іздеу дихотомиялық болуы мүмкін, бұл үшін таблица реттелген болуы керек.

Жаңа аттар таблицаға қосылады «бір-бірлеп», және әрбіруінің қосылғаннан кейін таблицфның реттелуі қалпына келтірілуі керек, алгоритмді сорттау қолдану, шығушы реттелген мәліметтер.

Бұл түсінік басқа таблицаға қатысы бар, жұмыс барысында Ассемблерде үлкен мүлшердегі таблица және сыртқы жадыға орналастыру және күрделі әдістер оның организацясын қолданылады. Мысалы, -В+ ағаш.

2. LL (1) грамматикалық анықтамасы.

Бұл идеяның логикалық жалғасуы, рекурсивтік көшуге байланысты, ол енгізу тізбегінде бірнеше символдарды қолданумен қатар, альтернативті біреуін ғана қолданумен түсіндіріледі. Егерде альтернативті алгоритмді таңдайтын болсақ, онда ереже бойынша, грамматикалық әртүрлі тізбектері бар екендігін көреміз. Сонымен қатар грамматикалар классы пайда болды, бұл негізгі принципке арналған- альтернативті бір тізбекті таңдасақ, онда көршілік мүмкіндіктердің негізінде бірнеше кезекті тізбек символдарын кездестіреміз. Бұл тізбекті біз LL (1) грамматикасы деп атаймыз. Шынымен, жұмыс алгоритмі бұларға өте оңай келмейді, қарастырылған жоғарыдағы алгоритм рекурсивті өтуге сәйкес келеді.

Грамматика LL(k),k>0 деген қасиетпен иемденген. Егер әрбір шығару қадамы бірмағыналы, кезектіальтернативті МП- автоматында жеткілікті стектегі символдармен берілсе, онда бірінші қарастырылған k символы ағымдағы қалыптан енгізу тізбегіндегі символдарға беріледі.

Бұл грамматика LL(k) грамматикасы деп аталады, егер ол LL(k) қасиетімен k>0 болса.

LL (1) атының өзі анықтамалық мағына береді.Бірінші литер ‘left’ сөзінен шыққан және мынадай мағына береді: енгізу тізбегі символдармен оқылады солдан оңға қарай. Екінші литер сонымен қатар ‘left’ сөзінен шыққан және мынадай мағына береді: жұмыс барысында солжақтық шығару қолданылады. (1) орына грамматика классының аты бүтін санмен беріледі, ол мынаны көрсетеді, қарастырылған қаншама символ бірмағыналы альтернативті болуы тиіс. Сонымен қатар LL(1) грамматикасы,LL(2) грамматикасы және т.б класстар да бар. Барлық LL(k) грамматикасы k>0 болғанда LL грамматикасына жатады. Бұл грамматикалдағы енгізу тізбегіндегі алгоритмді өңдеу, «к» алгоритмдік атаумен белгіленген. Оның орындалу принципі көбінесе МП – автоматының айырмашылығымен және әрбір қадамның жұмысты к символымен қарастыруын береді.

LL(1) грамматикасына келесі қасиеттер тән:

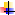Барлық LL(1) грамматикасы, әрбір k>0 –де бірмағыналы болуы керек.

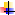LL(1) грамматикасының к-санында анықталғаның немесе анықталмағаның қадағалайтын немесе тексеретін алгоритм бар. Сонымен қатар, айқын, барлық граммаикалар рекурсивтік көшіруде белгілі- бір әдіспен LL(1) грамматикасының ішкі классы болып табылатындығы мәлім. Яғни, әрбір грамматика рекурсивтік көшуде белгілі –бір әдіспен LL(1) грамматикасында анықталады.

Барлық LL(1) грамматикалары солжақтық шығаруда қолданылады, сонымен қатар альтернативті алгоритмде олар солжақттық рекурсияға көшеді. Солжақтық рекурсия грамматикасы болып LL-грамматикасы болады. Ізінше, бірінші жұмыс болып, LL-грамматикасының класстары өте кең, бірақ ол жеткіліксіз.

Ол программалау тілдерінде синтаксистік конструкцияда мүмкіндіктері мол болады. Белгілі, kc – тілінде детерминал LL(k) – грамматикасымен беріледі. Бірақта LL-грамматикасын қолдануға өте ыңғайлы. Оны сызықтық характеристикамен құрылады.

LL (1) грамматикасының алгоритмін өңдеу.

LL (1) грамматикасы үшін жұмыс алгоритмі өте оңай. Ол екі шартпен бекітіледі, ол қадамдарды таңдауда альтернативте тексеріледі. Мәліметтерді шығаруда бұл шарттарға сәйкес символдарда беріледі және МП – автоматында есептеледі.

Бұл шарттарды былай анықтауға болады:

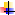Альтернативті ереже бойынша А→х, егер а€FIRST(1,x)

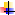Альтернативті ереже бойынша А→λ, егер а€ Follow(1,A)

Егер бұл екі шарттың екеуі де орындалса, онда тізбек МП- автоматында берілген тілде оқылмайды.

LL (1) грамматикасындағы шарт қатты болып келеді. Осы көптеген грамматикалар LL (1) грамматикасының класстары болып есептеледі. Мысалы, ең қарапайым грамматика G({a},{S},S) бұл шартқа сәйкес келмейді. Кейбір кезде грамматиканы құру ережесі, олардың LL (1) грамматикасын шығаруда айқындалады. Мысалы жоғарыда көрсетілген грамматика G(a) түрінде туындаған. Мұндай формадағы LL (1) грамматикасымен түсіндіріледі.

МП-автоматтың жұмысын программалау үшін, енгізу тізбегінде келесі тілдік символдарды өңдеу керек. Бұларға екі ережеден беріледі. Бұл екеуі де терминалдық символдардан басталады. Бұл түрді λ ережесін қосып, өзгертейік. Нәтижесінде жаңа грамматика аламыз.

P:

S→TR

R→λ|+TR|- TR

T→EF

F→λ|*EF|/EF

E→S|a|b

G-құрылған грамматикасы G шығару грамматикасында эквиваленцияланады. Бұған көз жеткізуге болады, егер λ- ережесінің алгоритмін қолдансақ, келтірілген грамматикалар G- грамматикасын береді, ол шарт бойынша берілген алгоритм болады. Осыған орай біз эквивалентті грамматиканы аламыз, бірақ ол формальді әдіспен алынбаған.

Бұл грамматика LL (1) грамматикасы болып табылады. Бұған көз жеткізу үшін, FIRST және Follow көпшілігін құрайық.

FIRST көпшілігін құру үшін, шығаруда G- грамматикасын қолданады. Ары қарай алгоритмдер қарастырылады, олар формальді түрде орналсқан.

Бұл жағдайда дайындықты барлық шығару мәләметтерінде формальдауға болады және автоматтандыруға болады.

Бұл іс-әрекеттерді компьютер көмегімен орындауға болады.

Рекурсивтік түсу.

Рекурсивтік түсу, көптеген әйгілі трансляторда қолданылады, ол синтаксистік талдаудың ең бірінші детерминироваланған әдісі болып табылады. Бұл әдістің кең қолданылуы, ол орындалуға өте жеңіл, егер компиляторды жазуда программалау тілді қолданады, рекурсивтік процедураларда қолданылады.

Рекурсивтік түсудің негізгі әдісі, әрбір грамматиканың терминалсыздығына процедура сәйкес келеді, ол процедура терминалсыздықты тудыратын тізбекті анықтайды. Сондықтан, МП – түрлендіргіштің модельдеуі рекурстік процедуралардың механизмімен алмасады. Жоғарғы деңгейдегі тілдер қиын стектік механизмдерді қолданады, МП – автоматы орындалуына қарағанда. Рекурсивтік түсудің әдісі уақыт мөлшерін және жадының синтаксистік сараптаудың әдісіне қарағанда жол береді.

Рекурсивтік түсудің әдісі кез – келген LL(1) – грамматикасына қолданылады, ол баламалық оң бөлшектерінің формасында жазылу керек.

Pascal программалау тілін рекурсивтік түсу әдісінің орындалуын көрсету үшін қолданайық. Синтаксистік анализатордың Recurs Method басты модулі, рекурсивтік түсудің әдісін орындайтын, процедураларды шақырады, кіру тізбегі бастапқы грамматиканың символы арқылы жаратылуын тексереді. Егер кіру тізбегі грамматикасымен шығарылған тілге жатса, онда Access (Кіру рұқсаты) процедурасы орындалады, әйтпесе Error (Қате) процедурасы орындалады. Осы кезде кіру тізбегі арнайы символмен аяқталуы тиіс – соңғы маркермен, мысалы (L). Соңғы маркердің кіріспесі қосымша грамматика ережесінің түрінің S’→S. қосылуына сәйкес келеді.

Алгоритмнің жұмысын орындау үшін Next Symb функциясы болу керек, ол кіру тізбегінің символын оқиды және бұл символдың өзгергіш Symb символының мағынасын иемденеді. Процедураларды құрғанда тізбектерді анықтау үшін, грамматиканың терминалсыз символдарымен жасалынған, келесі ережелерге сүйену керек:

Егер ағымдағы символмен грамматика ережесінің оң бөлігінде терминалсыздық болса, оған процедураның шақыруы сәйкес келеді, бұл терминалсызбен жаратылған тізбекті анықтайды.

Егер ағымдағы символмен грамматика ережесінің оң бөлігінде терминал болса, оған шартты оператор сәйкес келеді, терминалдың сәйкес келуіне тексеруді жүзеге асыратын грамматиканың ережелерінен және ағымдағы символдың мағынасы Symb өзгергіштен. Егер символдар сәйкес келсе, онда Next Symb процедурасының шақыруы орындалады, болмаған жағдайда келесі баламаға өту жүзеге асады. Егер барлық баламалар таусылса, Error процедурасының шақыруы орындалады.

Ереженің бос оң бөлімдері процедураның соңына өту талапқа сай болады. Мысалға G1 грамматикасының рекурсивтік түсу әдісімен синтаксистік анализатордың жазылуын көрейік.

Е→ТE’

E’→ +TE’| ε

T→PT’

T’→*PT’| ε

P→ (E) | I

Грамматиканың ережесін тағы бір ережемен толықтырайық. S → E 1.

G1 грамматикасына рекурсивтік түсуді орындауға арналған процедура 1.1 листингіде көрсетілген.

Листинг 1.1

Procedure Recurs_ Method (List_ Token: tList);

(List_ Token – кіру тізбегі)

Procedure Proc_E;

Begin

Proc_ T;

Proc_ E1

End (Proc_ E);

Procedure Proc_ E1;

Begin

If Symb = ‘+’ then

Begin

Next Symb

Proc_ T;

Proc_ E1

End

End ( Proc_ E1);

Procedure Proc_ T;

Begin

Proc_ P;

Proc_ T1

End ( Proc_ T);

Procedure Proc_ T1;

Begin

If Symb = ‘*’ then

Begin

Next Symb

Proc_ P;

Proc_ T1

End

End ( Proc_ T1);

Procedure Proc_ P;

Begin

If Symb = ‘(’ then

Begin

Next Symb;

Proc_ E;

If Symb = ‘)’ then

Next Symb;

Else

Error

End

Else

If Symb = ‘i’ then

Next Symb

Else

Error

End (Proc_ P)

Begin

{анализдің басында Symb өзгергішінің құрамында тізбектің бірінші символы болады}

Proc_E;

If Symb = ‘i’ then

Access

Else

Error

End (Recurs _ Method);

КС – грамматикасының эквиваленттік өзгеруі.

Тәжірибеде көргендей, шығару қиындықтарын шешу тек КС – грамматикасына анықталған шек қою арқылы ғана мүмкін.

Дәлелденген, КС – грамматиканың эквиваленттік проблемасы алгоритмдік шешілмейтін болады. Бірақ КС – грамматиканың пайдалы эквиваленттік өзгертулердің қатары болады. Бұл тілдің талдалуын жеңілдетуге әкеледі. Грамматика өзгертулерінде мынаны ескеру қажет, грамматика тілдің синтаксистік құрылымын анықтайды, сондықтан оның кез-келген өзгкертулері осы құрылымның өзгеруіне әкеледі.

Керексіз символдардың жойылуы.

Алгоритм 1.1 Жиынның анықталуы, КС – грамматиканың терминалсыз өндіретіндер символдары.

Кіру: КС – грамматика G=(N, ∑, P, S).

Шығу: Терминалсыз символдардың жиыны

Np={A| A→ + x, A ε N, x ε ∑+}

Алгоритмнің бейнеленуі:

□ Терминалсыз өндірудің рекурсивтік жиынды құру N p, N p,…; N p,…

Келесі түрде:

1. Қою N p = Ø, i=1.

2. Қою N p=N p {A| A→ ά ε P, ά ε (N p ∑)+}

3. Егер N p≠ N p, қоямыз I = i+1 және 2 –ші қадамға өту.

4. Қою Np = N p

Алгоритм 1.2 Жиынның анықталуы КС – грамматиканың орындалатын символдары.

Кіру: КС – грамматика G=(N, ∑, P, S).

Шығу: орындалатын символдардың жиыны Nr ={X| S→ άΧβ, X ε (∑ N), ά,β ε (∑ N)*}

Алгоритмнің бейнеленуі:

□ орындалатын символдардың рекурсивтік жиынын құру.

1. Қою N r = {S}, I = 1

2. Қою N r = N r {X | A → άΧβ ε R және A ε N r}

3. Егер N r≠ N қою I = i+1 және 2-ші қадамға өту.

4. Қою Nr = N r

Алгоритм 1.3 Керексіз символдарды жою.

Кіру: КС – грамматика G=(N, ∑, P, S), L(G)≠ Ø үшін.

Шығу: КС – грамматика G=(N’, ∑’, P’, S), онда L(G)≠ Ø және керексіз символдар жоқ.

Алгоритмнің бейнеленуі:

1.G грамматиканың Np терминалсыз жиынын құру.

2. Қою G1= (Np, ∑, P1, S), онда P1 P жиынының ережелерінен тұрады, құрамында тек символдары бар.

3. N1 жиынын құру, G1 грамматика символдарының орындалуы.

4. Қою G’ = (N ’, ∑’, P’, S), онда. P1 жиынының ережелерінен тұрады, құрамында тек Nr жиынының символдары бар.

КС – грамматикадағы керексіз символдарды жою үшін 1.1.және 1.2 алгоритмдерін 1.3 алгоритмнің тәртібі бойынша орындау керек. Бұл дегеніміз басында өндірмейтін терминалсыздықты алу, ал содан кейін орындалмайтын символдарды. Егер бұл алгоритмдердің қолданылу тәртібін өзгертсек, онда КС – грамматиканың құрамында керексіз символдар болуы мүмкін.

Бейнеленудің грамматикасы.

LR (K) – грамматикасының класс тармағы болады, ол бейнелеудің грамматикасы деп аталады. Бейнелену грамматикасының негізгі белгісі, олар үшін үлгі алгоритмін құру оңай. Синтаксистік сараптаудың тәсілдері, негізгі осындай грамматикаларда салынған.

Синтаксистік анализдің өрлеп келе жатқан әдістерінде сентенциалдық ағымдағы түрде ά негізгі іздеуі орындалады, ол А → ά грамматикасының ережесімен сәйкестікте терминалсыз А символына оралады. Өрлеп келе жатқан синтаксистік талдаудың негізгі проблемасы терминалсыз символдың және негізді іздеуде болады.

Бейнелеу қатынасының түсінігі.

Сентенциалдық форманың тек 2 көршілес символды қарастырғанда, негіздің соңы мен басын табу. Сентенциалдық форма бар άX1X2β онда, X1,X2εN ∑. Немесе талдаудың кейбір кезеңінде X1, символы немесе X2 символы, немесе олар бірігіп негізге кіру керек. Келесі үш оқиғаны қарастырайық:

Х1 – негіздің бөлімі, Х2 символы негізге кірмейді. Х1 символы Х2 символына қарағанда ертерек оралады. Бұл жағдайда айтады, Х1 символы Х2 символынан бұрын болып өтеді және оны былай жазады Х1· >X2. Осыдан айқындалатыны Х1 символы – негіздің соңғы символы (негіздің соңы), кейбір ереженің оң жақ бөлімінің соңғы символы, ал Х2 символы – терминалдық символ.

Екі Х1 және Х2 символдары негізге кіреді, бірге оралады. Әдетте бұл фактті былай белгілейді Х1=Х2. Бұл жағдайда символдар Х1 және Х2 грамматиканың кейбір ережелерінің оң жақ бөліміне кіруі керек. Х2 символы – негіздің бөлімі, ал Х1 негізге кірмейді. Х2 символы Х1 символына қарағанда ертерек орануы керек. Оны былай жазады Х1< ·Х2. Айқынды, бұл жағдайда Х1 – символы ол негіздің бірінші символы (негіздің басы), бұдан кейбір ереженің оң жақ бөлігінің бірінші символы.

(<·), (=) және (·>), мына символдармен белгіленетін қатыстар, бейнелеудің қатынастары деп аталады.

Грамматиканы ережемен қарастырайық:

(1) S → bAb (3) A → a

(2) A → cB (4) B → Aad

Грамматика символдардың арасындағы қарым – қатынасты анықтау үшін кейбір сентенциалдық түрінің жиынын қарастыру керек.

Сентенциалдық bcBb bcAadb

Түр bab

S S S

b b

b b A

Синтаксистік b A b

Ағаш c B d B

a A d

a

Негіз a cB Aad

c<A

b<a b<c A=a

Ағашпен анықталатын a>b c=B a=d

қатынас B>b d>b

Қарапайым грамматиканың белгіленуі.

Қарапайым белгілеуге негізделген синтаксистік анализ, άβώ тізбегінің 3 қатысын шығаруда қолданылады. (<·), (=) және (·>) келесі түрде

□ Егер β – негіз, онда көршілес ά тізбек символдарының арасында (<·) немесе (=) қатынас орындалады;

□ ά тізбегінің соңғы символы арасында және β тізбегінің 1 символының арасында (<·) қатысы орындалады;

□ негіздің көршілес символдардың арасында (=) қатысы орындалады;

□ β тізбегінің соңғы символы арасында және ώ тізбегінің 1 символы арасында (·>)қатысы орындалады;

КС – грамматикасы үшін бейнелену қатынасы G=(N, ∑, P, S). жиында анықталады. (N ∑ { })X (N ∑ { ε }) келесі түрде:

▪ X< ▪Y, егер P грамматика ережесінің жиынында A→αXBβ ережесі және шығуы бар болса B+Yγ;

▪ X=Y, егер P – да A→αXγβ түрдегі ереже бар болса;

▪ X ▪>a, егер P- да A→αβγβ түрдегі ереже бар болса және шығу бар болса;

▪ < ▪Х барлықтарға арналған Х, әрбір үшін S→ +X α;

▪ Y ▪>E барлықтарға арналған Y, әрбір үшін S → +α Y;

Сол жақ рекурсияны жою.

Программалау тілдерінде рекурсиямен және рекурсивті алгоритмдермен танысайық.Рекурсия-абстрактілі ойлау қабілетін дамытады,әртүрлі түрлерде (математикада,синтаксистік анализде,трансляцияда,көне өңдеуде,құрылымды мәліметтерді өңдеуде,шахматтық есептерде қолданылады.)Оларды қолдану процесстермен жүзеге асады.Алгоритм рекурсивті болады.

Егер ол өз-өзімен рекурсивті болса,тағы да алгоритм тік рекурсивті болады.Егер ол өзін-өзі орындаса,математикада белгілі мысалдардың бірі-рекурсивті алгоритм болып факториалды функция есептеледі.Бұл анықтама мына түрде болады:

F(n)=n+f(n-1), егер n>0

F(0)=1

Мұндағы F(n) функциясы f(n-1) функциясынан өтеді,ол f(n-2) функциясын анықтайды. Осыған орай,бұл мысалда рекурсия F денгейді құрайды.Осындай процесс шексіз болу үшін рекурсивті анықтама айнымалыны анықтауы керек

Рекурсивтік алгоритмдерді жазуда шартты мағыналарда Маккрати формасында қолдануға болады.Ол мынадай түрде болады:

[b1-a1,b2-a2,…bn-1-an-1,an], bi(i=1.2…n-1) шарты мағына береді.Шартты айтылудың мағынасы солдан оңға қарай шартпен есептеледі.Ол bi шарты табылмағанша,аі мағына береді.Маккарти формасына мысал ретінде н-факториалын алуға болады.

F(n)=[(n>1)-n+f(n-1),1]

В-рекурсивтік алгоритмін қарастырайық.

Алг длинцел в

Мағынасы

Басы

Егер n>1

Онда

f-n+f(n-1)

Сонда

f-1

соңы

Программалаушы бұл жазылымды нақты реттік анықтамаға сәйкес орындалады.

Алг длинцел faktorial

Мағынасы n

Длинцел р,к

Басы

Р-1

К үшін 2 n 1 қадамы орындалады.р-р+к

Цикл соңы

Factorial-p

Соңы

Рекурсивтік функция автоматты түрде локальда обьектілермен байланысады. Әрқашан рекурсивтік алгоритм ағымдағы локальды мағынамен беріледі. Ереже облысында аттар әрекеті идентификаторда орналасады.

Басқа мысал болып рекурсивтік алгоритмдердің Евклид алгоритмлерінде жұмыс істеуі болып табылады.

Бұл қарапайым әдісте рекурсия терендігі мысалымызда мағынасын береді. Жазылымда Евклид алгоритмдік рекурсиясы мына түрде болады.

Gcd(u,v)=[(v=0)-u,gcd(v,u mod v)]

Алг длинцел gcd

Мағынасы a,b

Длинцел u,v

Басы

u-(a) v-(b)

Егер v=0

Онда

Gcd-u

Сонда

Gcd-gcd(v,u,mod v)

әйтпесе

соңы егер

қайтымды болса,

соңы

алгоритмнің орналасуы

алгоритм Euclid_recursive

алг длинцел gsd

конст one-‘----------------------------‘

длинцел a,b

басы

шығару two

шындыққа шығару

шығару a,b

енгізу ch=’y’

шығару two

егер ch=’y’

цикл-соңы

шығару two

соңы

Қорытындылай келе Герон рекурсивтік алгоритмін Маккарти формасында жазайық.

Heron (a,x, )=[(x-a/x)/2)< -x,heron(a,(x+a/x)/2)]

Алг зат

Мағынасы a,x

Басы

Егер [(x-a/x)+0.5]<x

Онда

Heron-x

әйтпесе

heron-heron (a,(x+a/x)+0.5)

соңы егер

қайтымды болса,

соңы

Енгізілген синтаксистік талдау.

Барлық әдістер синтаксистік анализде процессордың құрылымын құруда және өзінің кейбір жұмысында КС-граматикасын қолданынылады.

Не нашли, что искали? Воспользуйтесь поиском: