Наращение процентов, налоги и инфляция (простые и сложные проценты)

В рассмотренных выше методах определения наращенной суммы не учитывались такие важные моменты, как налоги и инфляция.

Налог на полученные проценты. В ряде стран полученные (юридическими, а иногда и физическими лицами) проценты облагаются налогом, что, естественно, уменьшает реальную наращенную сумму. Нельзя не учитывать и то, что частый пересмотр налоговых правил вносит существенный элемент неопределенности в конечные результаты наращения для владельца денег[3].

Обозначим, как и выше, наращенную сумму до выплаты налогов (tax-free) через S, а с учетом выплаты как S". Пусть ставка налога на проценты равна g.

При начислении простых процентов находим:

S" = S - (S - P) g - S (1 - g) + Pg = P [1 + n (1 - g)i ].

Таким образом, учет налога сводится к соответствующему сокращению процентной ставки: вместо ставки i фактически применяется ставка (1 - g) i.

В долгосрочных операциях при начислении налога на сложные проценты возможны следующие варианты: налог начисляется за весь срок сразу, т.е. на всю сумму процентов, или последовательно, например в конце каждого года. В первом случае сумма налога равна P [(1 + i) ⁿ - 1] g, а наращенная сумма после выплаты налога

S" = S - (S - P) g = S (1 - g) + Pg = P [(1 - g)(1 + i) ⁿ + g ]. (2.38)

Во втором случае сумма налога определяется за каждый истекший год. Очевидно, что она является переменной величиной, так как сумма процентов увеличивается во времени. Соответственно увеличивается и годовая сумма налогов. Сумма налогов за весь срок, очевидно, не зависит от метода начисления.

Налог за год t (обозначим его как G_t) можно найти с помощью следующего рекуррентного выражения:

G_t = I_tg = (S_t - S_{t- 1}) g = P [(1 + i) ^t - (1 + i) ^{t -1}] g. (2.39)

Пример 2.21. Пусть ставка налога на проценты равна 10%. Процентная ставка — 30% годовых, срок начисления — три года. Первоначальная сумма ссуды — 1000 тыс. руб. Определим наращенную сумму с учетом выплаты налога на проценты.

При начислении простых процентов за весь срок получим: наращенная сумма без уплаты налога S = 1900 тыс. руб., с учетом его выплаты в конце срока S" = 1000(1 + 3 х 0,9 х 0,3) = 1810 тыс. руб., сумма налога 90 тыс. руб.

Начислим теперь сложные проценты. Наращенная сумма без уплаты налога S = 2197 тыс.руб., с учетом его выплаты S'' = 1000[(1 - 0,1)(1 + 0,3)³ + 0,1] = 2077,3 тыс.руб.

Сумма налога равна 119,7 тыс. руб., причем согласно формуле (2.39) за первый год выплачивается 1000(1,3¹ - 1,3⁰)0,1 = 30 тыс. руб., за второй год — 1000(1,3² - 1,3)0,1 = 39 тыс. руб., за третий год - 1000(1,3³ - 1,3²)0,1 = 50,7 тыс. руб.

Инфляция. В рассмотренных выше методах наращения все денежные величины измерялись по номиналу. Иначе говоря, не принималось во внимание снижение реальной покупательной способности денег за период, охватываемый финансовой операцией. Однако в современных, особенно российских, условиях инфляция часто играет решающую роль и без ее учета конечные результаты представляют собой весьма и весьма условную величину.

Инфляцию необходимо учитывать по крайней мере в двух случаях: при расчете наращенной суммы денег и при измерении реальной эффективности (доходности) финансовой операции. Остановимся на этих проблемах.

Прежде всего напомним, что изменение покупательной способности денег за некоторый период измеряется с помощью соответствующего индекса J_nc. Пусть S — наращенная сумма денег, измеренная по номиналу. Эта же сумма, но с учетом ее обесценения составит:

C = S х J_nc.

Индекс покупательной способности денег, как известно, равен обратной величине индекса цен:

Разумеется, указанные индексы должны относиться к одним и тем же временным интервалам. Пусть, например, сегодня получено 150 тыс. руб., известно, что за два предшествующих года цены увеличились в три раза, т.е. J_p = 3. В этом случае индекс покупательной способности денег равен 1/3. Следовательно, реальная покупательная способность 150 тыс. руб. составит в момент получения всего 150 х (1/3) = 50 тыс. руб. в деньгах двухлетней давности.

Нетрудно связать индекс цен и темп инфляции. Предварительно напомним некоторые понятия. Под темпом инфляции обычно понимается относительный прирост цен за период; обозначим его как H; измеряется он в процентах. Темп инфляции и индекс цен связаны следующим образом:

Н = 100(J_p - 1).

В свою очередь

Например, если темп инфляции равен 130%, то цены за этот период выросли в 2,3 раза.

Среднегодовые темп роста цен (i_p) и темп инфляции (h) находятся на основе величины J_p как:

Поскольку инфляция является цепным процессом (цены в текущем периоде повышаются на h_t процентов относительно уровня, сложившегося в предыдущем периоде), то индекс цен за несколько таких периодов равен произведению цепных индексов цен:

(2.40)

Пусть теперь речь идет о будущем. Если h — постоянный ожидаемый (или прогнозируемый) темп инфляции за период, то за n таких периодов получим

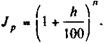(2.41)

Грубой ошибкой, которая, к сожалению, встречается в российской практике (даже в экономических публикациях, претендующих на научность!), является суммирование темпов инфляции для получения обобщающего показателя инфляции за период. Это, кстати, заметно снижает величину получаемого показателя.

Пример 2.22.

а) постоянный темп инфляции на уровне, скажем, 10% в месяц за год приводит к росту цен в размере J_p = 1,1¹² = 3,1384, таким образом, годовой темп инфляции равен 213,84%, а не 120%;

б) последовательный прирост цен по месяцам составил 25; 20 и 18%.

Индекс цен за три месяца согласно формуле (2.40) равен 1,25 х 1,2 х 1,18 =1,77. Темп инфляции за три месяца составил 77%.

Вернемся к проблеме обесценения денег при их наращении. В общем случае теперь можно записать:

(2.42)

Если наращение производится по простой ставке, имеем:

(2.43)

Как видим, увеличение наращенной суммы с учетом сохранения покупательной способности денег имеет место только тогда, когда 1 + ni > J_p.

Пример 2.23. Допустим, на сумму 1,5 млн. руб. в течение трех месяцев начисляются простые проценты по ставке 50% годовых (K = 360). Наращенная сумма равна 1,6875 млн. руб. Если ежемесячная инфляция характеризуется темпами, приведенными в примере 2.22,б, то с учетом обесценения наращенная сумма составит всего 1,6875/1,77 = 0,9534 млн. руб.

Обратимся теперь к наращению по сложным процентам. Подставив в формулу (2.42) значения S и J_p, находим

(2.44)

Величины, на которые умножается Р в формулах (2.43) и (2.44), представляют собой множители наращения с учетом инфляции.

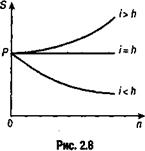
Посмотрим теперь, как влияют ставка процента i и темп инфляции h на величину C. Очевидно, что если среднегодовой темп инфляции равен ставке процентов, то роста реальной суммы не произойдет: наращение будет поглощаться инфляцией и, следовательно, С = Р. Если же h /100 > i, то наблюдается "эрозия" капитала, его реальная сумма будет меньше первоначальной. Только в ситуации, когда h /100 < i происходит реальный рост (рис. 2.8).

Возникает вопрос: при какой процентной ставке наращение будет только компенсировать инфляцию? Если речь идет о простых процентах, то, приравняв множитель наращения с учетом инфляции в формуле (2.43) к единице, находим минимально допустимую (барьерную) ставку:

Для сложных процентов искомую ставку определим на основе формулы (2.44). Получим i * = h. Ставку, превышающую i *, называют положительной ставкой процента.

Пример 2.24. По данным примера 2.23 найдем минимально допустимую величину ставки. Напомним, что индекс цен за три месяца был равен 1,77.

= 3,08, или 308% годовых.

Таким образом, только ставка, превышающая 308 % годовых, будет в данных условиях приносить реальный доход.

Владельцы денег, разумеется, предпринимают различные попытки для компенсации обесценения денег. Наиболее распространенной является корректировка ставки процентов, по которой осуществляется наращение, т.е. увеличение ставки на величину так называемой инфляционной премии, иначе говоря, производится индексация ставки. Итоговую величину можно назвать брутто-ставкой. (В западной финансовой литературе такую ставку часто называют номинальной. Однако этот термин уже "занят" — см. параграф 2.3.)

Обсудим методы определения брутто-ставки. Если речь идет о полной компенсации инфляции в размере брутто-ставки при начислении простых процентов, то необходимую величину находим из равенства

,

где r — брутто-ставка.

Отсюда

(2.45)

Пример 2.25. По данным примеров 2.23 и 2.24 получим

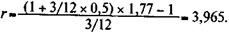
Таким образом, простая ставка, равная 396,5% годовых, не только компенсирует инфляцию, но и обеспечивает реальную доходность, равную 50% годовых.

Величину брутто-ставки для наращения по сложной ставке процента находим из равенства

.

Отсюда

. (2.46)

На практике ставку, скорректированную по темпу инфляции, часто рассчитывают иначе, а именно:

(2.47)

Формула (2.47) по сравнению с формулой (2.46) содержит один дополнительный член, которым при незначительных величинах i и h можно пренебречь. Если же они значительны, то ошибка (не в пользу владельца денег) станет весьма ощутимой. Например, даже при i = 5% и h = 10% "вклад" этого произведения в брутто-ставку составит 0,5%. Брутто-ставка в этом случае равна 15,5% вместо 15% по формуле (2.47). При годовой инфляции в 100% и той же ставке наращения брутто-ставка увеличивается до 0,05 + 1 + 1 х 0,05 = 1,1, т.е. до 110%, а не 105%.

Разумеется, что при высоких темпах инфляции корректировка (индексация) ставки имеет смысл только для кратко- или в крайнем случае для среднесрочных операций.

Перейдем теперь к решению обратной задачи — к измерению реальной ставки процента, т.е. доходности с учетом инфляции — определению i по заданному значению брутто-ставки. Если r — объявленная норма доходности (брутто-ставка), то искомый показатель доходности в виде годовой процентной ставки i можно определить при начислении простых процентов на основе (2.43) как

. (2.48)

Реальная доходность, как видим, здесь зависит от срока наращения процентов. Напомним, что фигурирующий в этой формуле индекс цен охватывает весь период начисления процентов.

Аналогичный по содержанию показатель, но при наращении по сложным процентам найдем на основе формулы (2.44):

. (2.49)

Если брутто-ставка определяется по упрощенной формуле (2.47), то

. (2.50)

Показатель доходности здесь не зависит от срока начисления процентов. Положительной ставка i может быть только при условии

при начислении простых процентов и r > h при начислении сложных процентов.

Пример 2.26. Найдем реальную ставку сложных процентов для условий: годовая инфляция 120%, брутто-ставка 150%:

= 0,1364, или 13,68% (по упрощенной формуле 30%).

Другой метод компенсации инфляции сводится к индексации первоначальной суммы платежа Р. В этом случае эта сумма периодически корректируется с помощью заранее оговоренного индекса. Такой метод принят в Великобритании. По определению

C = PJ_p (1 + i) ⁿ.

Не нашли, что искали? Воспользуйтесь поиском: