
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
ВЫЧИСЛЕНИЕ СУММЫ (СУММИРОВАНИЕ) ЭЛЕМЕНТОВ ВЕКТОРА
МИНИСТЕРСТВО ОБЩЕГО И ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
УФИМСКИЙ ГОСУДАРСТВЕННЫЙ НЕФТЯНОЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
КАФЕДРА ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ И ИНЖЕНЕРНОЙ КИБЕРНЕТИКИ
ОСНОВЫ АЛГОРИТМИЗАЦИИ
УФА 2000
В учебном пособии обсуждаются основные аспекты алгоритмизации. Оно служит основой для разработки схем алгоритмов при обработке одно- и двумерных массивов и решении некоторых других задач, таких как вычисление значений полиномов и суммирование рядов. Приводятся примеры для лучшего понимания проблемы разработки алгоритмов решения задач.
Учебное пособие может быть использовано для студентов всех специальностей заочной формы обучения УГНТУ.
Составители: ИВАНОВ В.И., доцент,
МУХАМАДЕЕВ И.Г., доцент,
ИВАНОВА О.В., гр. ЭА-96-01
Рецензент: ХОРОБРОВ В.Р., доцент
Ó Уфимский государственный нефтяной
технический университет, 2000
ВВЕДЕНИЕ
Процесс решения любой задачи на компьютере состоит из нескольких последовательных шагов или этапов. Наиболее важными из них являются следующие:
1) постановка задачи (формализация задачи);
2) алгоритмическая часть (алгоритмизация);
3) программирование;
4) оценка и анализ полученных результатов (контрольный расчет).
Решение любой инженерной задачи, основанной на законах и уравнениях физики, химии, биохимии, показывает, что наиболее сложной и трудоемкой частью является этап формализации (математического описания) задачи, что требует высокого уровня образования и квалификации исследователя.
Практика показывает, что адекватная формализация (математическое описание) достаточно сложных задач требует порядка 70% временных затрат для реализации задачи на компьютере.
Следующим важным этапом является алгоритмизация. Она предполагает разработку структурной (поблочной) графической схемы алгоритма в соответствии с заданием, которое было сформулировано (формализовано) на предыдущем этапе. Очевидно, что разработку графической схемы можно исключить для простой задачи, в частности, если ее решает опытный программист. Однако, схемы алгоритмов необходимо разрабатывать при решении задач высокой сложности и в любом случае для начинающих пользователей (студентов).
В данном учебном пособии рассматриваются некоторые проблемы алгоритмизации, а также типовые схемы алгоритмов.
Следующим этапом решения задачи на компьютере является собственно программирование. Для этой цели можно использовать алгоритмический язык высокого уровня, например, ПАСКАЛЬ.
Отметим, что программирование может быть наиболее простым этапом в ходе решения задачи на компьютере. Данный этап может быть легко реализован опытным программистом при наличии детализированной схемы алгоритма.
Задача считается решенной, если выполнены контрольные (проверочные) вычисления. При этом полученные на компьютере результаты вычислений обычно обсуждаются с квалифицированными специалистами (научными исследователями или преподавателями) для подтверждения того, что все ограничения и особенности задачи учтены.
АЛГОРИТМИЗАЦИЯ
Вначале рассмотрим два общих положения.
Первое
Существуют три основные (базовые) алгоритмические структуры:
1) линейная структура;
2) циклическая структура;
3) разветвленная структура.
Считается, что алгоритм любой степени сложности состоит из различных комбинаций упомянутых выше трех базовых структур
Наиболее простым и легким для понимания является алгоритм линейной структуры,  который представляет собой совокупность операций, следующих друг за другом. Алгоритм линейной структуры показан на рис. 1.
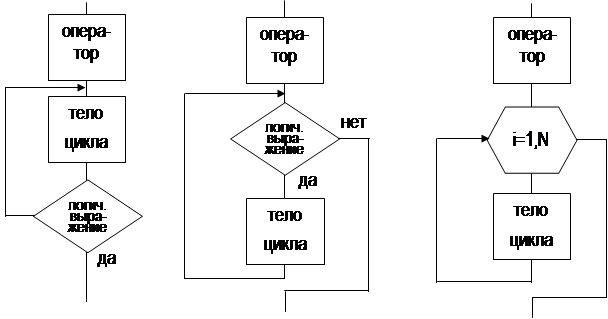
Алгоритм циклической структуры включает регулярно повторяющиеся операции, называемые “телом цикла”. Варианты оформления алгоритмов циклической структуры приведены на рис. 2. который представляет собой совокупность операций, следующих друг за другом. Алгоритм линейной структуры показан на рис. 1.
Алгоритм циклической структуры включает регулярно повторяющиеся операции, называемые “телом цикла”. Варианты оформления алгоритмов циклической структуры приведены на рис. 2.
| Рис.1 |
|
a) цикл "до" б) цикл "пока" в) арифметический цикл
Рис.2
Отметим, что арифметический цикл с параметром цикла i (вариант в) используется, когда число повторяющихся вычислений (циклов) N известно.
В алгоритмах разветвленной структуры вычислительный процесс формируется, как правило, в виде двух ветвей (путей) в соответствии с некоторым условием, которое может быть истинным (“да”) или ложным (“нет”). Варианты оформления алгоритмов разветвленной структуры приведены на рис. 3.
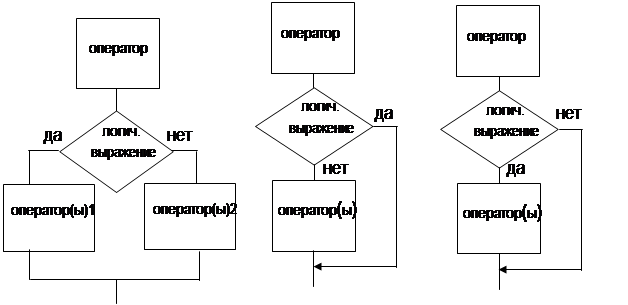 |
a) альтернатива б) обход б) коррекция
Рис.3
Второе
Обычно существует необходимость в уточнении исходного алгоритма, составленного из общих формальных соображений. В этом случае говорят о разработке детализированной схемы алгоритма методом последовательного уточнения (метод "сверху вниз").
Пример 1
Необходимо вычислить максимальное значение 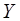 переменных
переменных 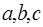 . Существует много различных способов решения данной задачи. Рассмотрим один из них с использованием дополнительной переменной
. Существует много различных способов решения данной задачи. Рассмотрим один из них с использованием дополнительной переменной 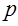 . Алгоритм примера 1 показан на рис. 4.
. Алгоритм примера 1 показан на рис. 4.
В этом примере, каждому блочному символу наиболее детализированной схемы алгоритма, полученной на 3-ем шаге уточнения, может быть поставлен в соответствие оператор алгоритмического языка высокого уровня.
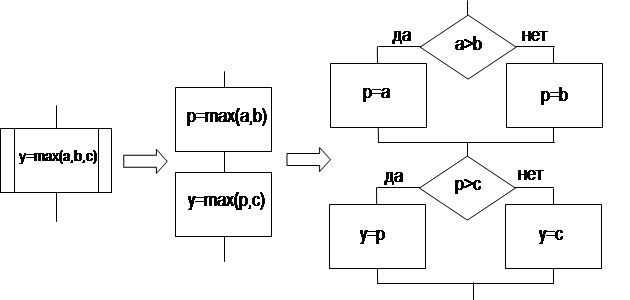
1 шаг 2 шаг 3 шаг
Рис.4
Далее рассмотрим типовые алгоритмы наиболее часто встречающихся задач при обработке одномерных и двумерных массивов данных.
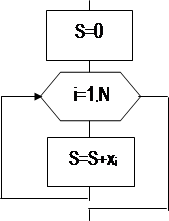
ВЫЧИСЛЕНИЕ СУММЫ (СУММИРОВАНИЕ) ЭЛЕМЕНТОВ ВЕКТОРА
Для вычисления суммы 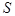 элементов вектора, предположим, X = {
элементов вектора, предположим, X = {  }, i = 1, 2,..., N, его значения и размерность N должны быть известныкак для данного случая, так и для последующих задач.
}, i = 1, 2,..., N, его значения и размерность N должны быть известныкак для данного случая, так и для последующих задач.
Очевидно,
Алгоритм суммирования элемен-тов вектора приведен на рис. 5. Отметим, что начальное значение суммы Покажем, как можно использовать данный типовой алгоритм для реше-ния более сложной задачи.
Не нашли, что искали? Воспользуйтесь поиском:
|
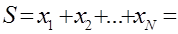
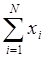 (1) (1)
(1) (1) .
.