Преобразование характеристик при интегрировании случайных процессов

Предварительно следует напомнить обучающимся изложенные на лекции характеристики интеграла от случайного процесса.

Пусть X (t) - случайный процесс,

.

Тогда выполняются следующие свойства.

1) .

2) .

3) , .

Пример 1. Дан с. п. X (t) = (t ² +1) U, U N (-3, 5), 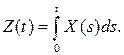Найти математическое ожидание m_Z (t), корреляционную функцию К_Z (t ₁, t ₂), дисперсию D_Z (t), взаимные корреляционные функции K_{Z , X} (t ₁, t ₂), K_{X , Z} (t ₁, t ₂), не интегрируя X (t).

Решение. Найдем математическое ожидание и дисперсию случайной величины U:

Найдем математическое ожидание с. п. X (t)

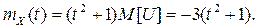
Найдем корреляционную функцию с.п. X (t)

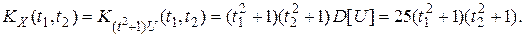
Найдем математическое ожидание с. п. Z (t) формуле 1) п. 7:

Найдем корреляционную функцию с. п. Z (t) по формуле 2) п. 7:

.

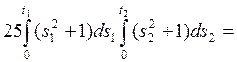
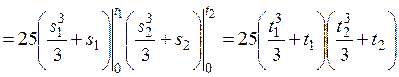Найдем дисперсию с. п. Z (t) по свойству 6) п. 4:

Найдем взаимные корреляционные функции по формуле 3) п. 7:

Пример 2. Найти корреляционную функцию К_Y (t ₁, t ₂), дисперсию D_Y (t), нормированную корреляционную функцию ρ_Y (t ₁, t ₂) случайного процесса Y (t)= X (t) + Z (t), не интегрируя X (t).

Решение. Найдем дисперсию случайной величины U:

Найдем корреляционную функцию с.п. X (t)

Найдем корреляционную функцию с. п. Z (t) по формуле 2) п. 7:

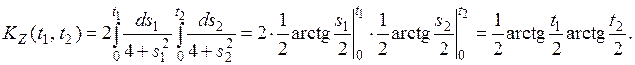
Найдем взаимные корреляционные функции с. п. X (t), Z (t) по формуле 3) п. 7:

Найдем корреляционную функцию с. п. Y (t) по формуле (1):

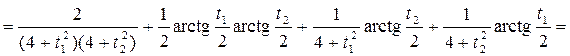
Найдем дисперсию с. п. Y (t) по свойству 6) пункта 4:

Найдем нормированную корреляционную функцию с. п. Y (t)

При этом знак совпадает со знаком выражения

.

Заключительная часть (5 мин). Преподаватель подводит итоги занятия. По результатам работы курсантов и проведенного опроса он определяет степень усвоения материала и оценивает работу обучающихся, дает задание на самоподготовку.

VI. Литература, рекомендованная преподавателю

Основная:

1. Вентцель Е.С., Овчаров Л.А. Теория случайных процессов и ее инженерные приложения: учебное пособие – 5-е изд., стер. – М.: КНОРУС, 2013. – 448 с.

2. Вентцель Е.С. Задачи и упражнения по теории вероятностей. – М.: Издательский центр «Академия», 2014. – 496 с.

3. Гмурман, В.Е. Руководство к решению задач по теории вероятностей и математической статистике: учебное пособие – 11-е изд., перераб. – М.: Высшее образование, 2013. – 404 с.

Дополнительная:

1. Артамонов В.С., Антюхов В.И. [и др.]. Системный анализ и принятие решений: учебник – под ред. В. С. Артамонова; МЧС России. – СПб.: СПбУ ГПС МЧС России, 2009. – 378 с.

2. Гмурман В.Е. Теория вероятностей и математическая статистика: учебное пособие–11-е изд. – М.: Пресса, 2009. –479 с.

3. Кремер Н.Ш. Теория вероятностей и математическая статистика: учебник для вузов – М.: ЮНИТИ -ДАНА, 2012. – 551 с.

VII. Приложение

Задание на самоподготовку:

1. Повторить материалы лекций и практического занятия по конспекту.

2. СП X (t) = t+ 1+ t ² U - V cos2 t,где U В (10, 0.2), V N (3;2) – некоррелированные случайные величины, Y (t)=2 X (t) – t ² X ¢(t). Найти математическое ожидание m_Y (t), корреляционную функцию K_Y (t ₁, t ₂), дисперсию D_Y (t), не дифференцируя X (t).

Разработал:

профессор кафедры, к.т.н.,

доцент Н.В. Каменецкая

Лист регистрации изменений

Не нашли, что искали? Воспользуйтесь поиском: